数字图像处理篇（6）边缘检测原理及其算子

目录

一、引言

1、图像中的求导

2、梯度

二、理想情况边缘检测

1、Roberts算子

2、Prewitt算子与Sobel算子

3、Laplacian算子

三、非理想状态下的边缘检测

1、LoG高斯-拉普拉斯算子        

2、canny算子

---

一、引言

        给定一张图像，我们如何去找到最显著的边缘呢？考虑下面这幅图中的彩色图像，如果有人让你指出最显著的边缘，你会追踪哪些边缘？

         定性的说，依据人眼的理性判断，我们所追踪的边缘可能会出现在那些颜色、亮度或者纹理不一样的区域之间。可是，电脑不像人眼，它又是怎么判断边缘的呢？

1、图像中的求导

        别慌！计算机没有脑子判断，但是计算机会做数学计算呀！我们想想，如果从数学的角度定义边缘，理想状况下，我们可以说边缘是图像强度函数f（x，y）中变化迅速的地方。可以通过计算函数导数的方式来找到强度函数迅速变化的点。导数值大，则说明变化越大；导数值等于0，则说明灰度值没有发生变化；导数值小，则说明灰度值变化小。如下图很形象的表示了这一层关系：

        由于图片内部是一个个像素构成，而不是连续值，所以我们求导也是取的离散导数（有限差分）。一共有三种一阶求导的方式：

①前向差分

                        ​​​​​​​        ​​​​​​​        ​​​​​​​        

②反向差分

                                                

③中心差分

                                                

二阶求导我们定义为：               

        

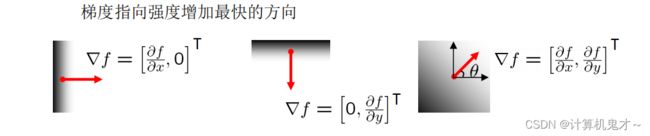
2、梯度

         那么根据微积分的知识，图像强度函数下降最快的方向即为梯度的方向，如果找到一种方法，能求出图片的梯度方向，是不是边缘检测的问题就迎刃而解了？

定义图像强度函数f在坐标（x，y）处的梯度定义为二维列向量：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        这个向量在位置（x，y）处的几何性质是它指向f的最大变化率方向。而该向量的幅值表示为M（x，y），是梯度向量方向的变化率在（x,y）处的值。同时M（x，y）是与原图像大小相同的图像，通常称这幅图为梯度图像。同时为了创造线性算子，我们把梯度的计算用绝对值来代替平方运算求和后进行平方根运算。如下面这个公式：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

二、理想情况边缘检测

        我们已经知道了边缘检测的数学逻辑，那么接下来需要我们去构造一个卷积核，与图像进行互相关运算来达到边缘检测的效果。由于下面这个图下文会经常见用到，我们在本篇博客中，统一将此图命名为图A。下面将介绍几种能够进行边缘检测的算子。

1、Roberts算子

        Roberts 算子是利用交叉差值寻找边缘的一种算子，是最简单的边缘检测算子之一。Roberts 算子利用对角线方向相邻两像素之差近似梯度值来检测边缘，检测垂直边缘的效果要优于其他方向边缘，定位精度高，但是也有一定的缺点，比如说是非对称的，无法检测45°倍数的边缘。

        依据引言部分的结论，我们知道，在图A中位置的一阶导数的最简近似值是以及,Roberts在早期数字图像处理开发中，却提出了另一种方式近似，我们称之为交叉差值。即把gx和gy替换为和​​​​​​​。

        根据梯度向量的幅值近似运算，我们可以想到也就是说，我们能构造出下面这个算子，我们称之为Roberts交叉梯度算子，简称为罗伯特算子。

        我们用之前学过的2D卷积函数对图像进行处理，处理的代码如下，不过大家可以先自己动动手，再来看小编的代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt
import random

#导入自己的图片，记得图片名改成自己的
img=cv2.imread("picture.jpg",-1)

#创造x与y方向的roberts算子
kernelX=np.array([[-1,0],[0,1]])
kernelY=np.array([[0,-1],[1,0]])

img1=cv2.filter2D(img,-1, kernelX, borderType=cv2.BORDER_REFLECT)
img2=cv2.filter2D(img,-1, kernelY, borderType=cv2.BORDER_REFLECT)
#将两个相加，形成M(x,y)
Roberts = cv2.addWeighted(img1, 0.5, img1, 0.5, 0)


cv2.imshow("x",img1)
cv2.imwrite("x.jpg",img1)
cv2.imshow("y",img2)
cv2.imwrite("y.jpg",img2)
cv2.imshow("roberts",Roberts)
cv2.imwrite("roberts.jpg",Roberts)

cv2.waitKey()
cv2.destroyAllKeys()

 小编得出的结果如下图（建议在暗处观察）：

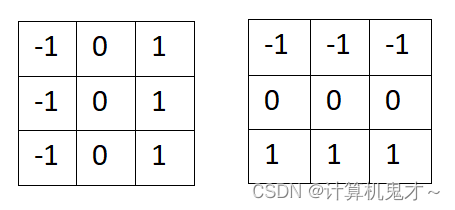
2、Prewitt算子与Sobel算子

        如我们前几节所述，我们更喜欢使用奇数卷积核，比如说3×3的、5×5的，一个最简单的思路就是，如果我们算x方向上的图像强度值变化，我们可以用它右边的强度值减去左边的强度值，即，同理，对于y方向上的有。同时，为了抵抗噪声（避免某个点的“突变”），我们选择将它周围的点也带入运算，也就是说，x方向上会变成。基于此思想我们可以得到下面的算子，称之为prewitt算子，其中左边这个是x方向上求梯度，右边这个是y方向上求梯度。

         如果我们再对这个算子进行一点提高，我们可能会想到在“平滑”中对每个点赋予权重这一思想。于是乎，我们将所在的这一行或者这一列赋予更高的权重。比如说2，此时就形成了应用更为广泛的sobel算子，还有其余权重下的算子，比如说scharr算子，其实与sobel大同小异，小编这里就不介绍了。

         同理，左边的是x方向上的梯度，右边的是y方向上的梯度。同时。我们期待在用这两个核进行图像处理后，图像的每一个点有正有负，所以我们期待能够先取绝对值，然后使大于255的值变为255。并且我们需要修改图像的深度，如果为8位的深度，256会被计算机进行“取余”运算，变成一个很小的值。并且由于有正有负，我们一般把深度调节为64位。

        除了使用2D卷积函数，其实在open-cv中有专门的Sobel函数如下：

dst = cv2.Sobel(src, ddepth, dx, dy[, dst[, ksize[, borderType]]])

参数及其含义：

dst：输出图像

src：输入图像

ddepth：图像深度，例如用cv2.CV_16S代表16位，-1代表保持不变

dx：在x方向上的求导阶数，取值为0或1

dy：在y方向上的求导阶数，取值同上。（如果dx为1，dy为0，代表求x方向上的梯度）

ksize：卷积核的大小

borderType：边缘样式

进行取绝对值的函数如下：

dst=cv2.convertScaleAbs(src[,alpha[,beta]]])

参数及其含义：

dst：输出图像

src：输入图像

alpha：调节系数

beta：调节亮度

稍微练练手，如下述代码：

import cv2
import numpy as np
import random

#记得改为自己图像的名字
img=cv2.imread("picture.jpg",0)

#算x方向的梯度
img1=cv2.Sobel(img,cv2.CV_64F,1,0)
img1=cv2.convertScaleAbs(img1)
cv2.imshow("x",img1)
cv2.imwrite("x.jpg",img1)

#算y方向上的梯度
img2=cv2.Sobel(img,cv2.CV_64F,0,1)
img2=cv2.convertScaleAbs(img2)
cv2.imshow("y",img2)
cv2.imwrite("y.jpg",img2)

#x方向与y方向梯度的结合
Sobel = cv2.addWeighted(img1, 0.5, img1, 0.5, 0)
cv2.imshow("sobel",Sobel)
cv2.imwrite("sobel.jpg",Sobel)

cv2.waitKey()
cv2.destroyAllKeys()

得到的结果如下图： 

3、Laplacian算子

        刚刚我们讲述的几种算子全是利用的一阶求导的方式，那么有没有使用二阶求导的算子呢？

        答案是肯定的，我们有,所以可以证明，两个变量的离散拉普拉斯算子是,即卷积核如下图：

         该算子能从四个方向上体现出，边界点的梯度值大，而非边界点梯度值小，同时也要去调整深度并且进行取绝对值的运算，大家可以自行验证该结论。小编这里科普一下open-cv里与之相关的拉普拉斯函数。

dst=cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])

参数及其含义：

dst：输出图像

src：输入图像

ddepth：深度

ksize：用于计算二阶导数的核尺寸大小

scale：缩放因子，默认为1，表示不缩放

delta：输出图像的偏移量，一般为0

borderType：边界样式，具体取值看小编以前写的文章

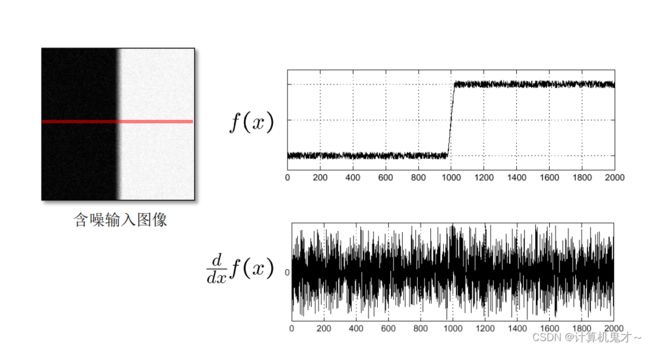
三、非理想状态下的边缘检测

        刚刚我们讨论了一般情况下的边缘检测原理及其实现方式，但是对于一些含有噪声的图片，我们如何去寻找边界？

边缘在哪里？

1、LoG高斯-拉普拉斯算子        

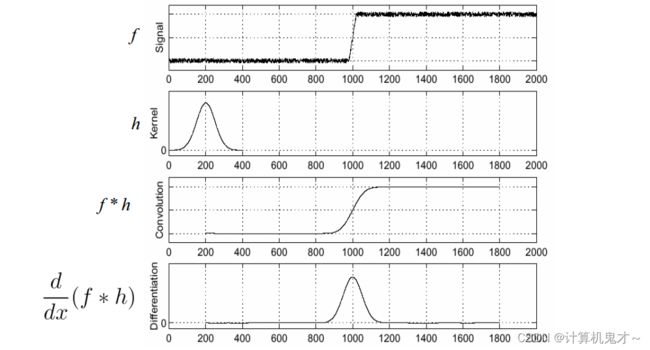
        在之前写过的文章中，我们说过，可以使用平滑操作处理图像，使噪点消除。最常见的线性平滑操作是进行高斯平滑。也就是说对被高斯核卷积后的图像进行边缘检测，而我们目前学的边缘检测最优方法是拉普拉斯算子。而卷积与微分具有结合性，即。这一性质为我们节省了一项操作。（也就是通过后的结果寻找到一个更为合适的核），我们把这个新得到的算子称之为LoG算子，也叫做高斯拉普拉斯算子。

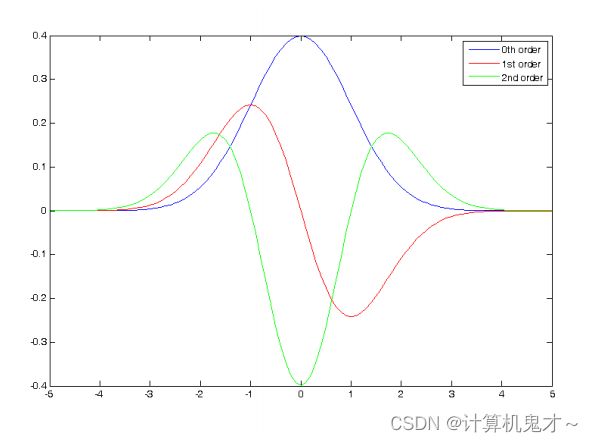
 高斯函数（蓝）、一阶高斯函数求偏导（红）以及二阶高斯函数求偏导（绿）后的结果：

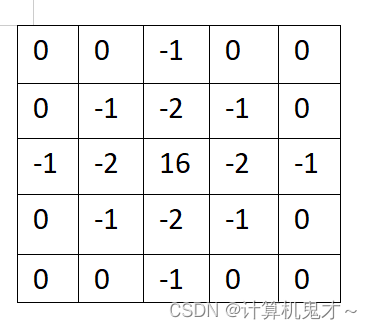
 如此一来，我们能够构造一个LoG算子，如下图

 在open-cv实战中直接用一个2D卷积就行了，相信大家都会，小编这里就不演示了。

2、canny算子

        下面将介绍一种更为复杂的边缘检测算子-------canny算子，它的一般流程如下：

        首先第一步，去躁，这一步很简单，直接用高斯滤波法，进行卷积处理即可，这里不做更多解释了。第二步，梯度运算，就是利用sobel算子求出每一个点的梯度幅值M（x，y）与方向θ（x，y）。第三步为非极大值抑制，它的作用是瘦边。即将该点处的M（x，y）值与正负几个像素值作比较，如果它是最大的才会显现出来，否则就会被“抑制”掉。第四部，选择两个阈值，maxVal以及minVal，大于maxVal的像素直接入选，小于minVal的像素直接pass掉。

        open-cv中相关函数：

edges=cv2.Canny(src,threshold1,threshold2) 

参数及其含义：

edges：得到边缘的图像

threshold1：第一个阈值

threshold2：第二个阈值

import cv2
import numpy as np


img=cv2.imread("p.jpg",0)
img1=cv2.Canny(img,210,50)

cv2.imshow("x",img1)
cv2.imwrite("x.jpg",img1)
cv2.waitKey()
cv2.destroyAllKeys()

得到的图片：

        本期的数字图像处理课就到此为止啦，点赞加收藏，带你学习更多数字图像处理的知识！