图的基本操作(C语言)

更新中。。。。。

1.邻接矩阵创建图

void AdjMatrix(int a[][MAX],int n,int e)//邻接矩阵存储图
{
	int i,j,k,weight;
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			a[i][j]=MaxValue;
		}
	}
	for(k=0;k<e;k++)
	{
		scanf("%d,%d,%d",&i,&j,&weight);
		a[i][j]=weight;
		a[j][i]=weight;
	}
}

2.邻接表创建图

void AdjMatrix(ArrayNode G[],int n,int e)//邻接表创建图
{
	int k,vi,vj,weight;
	EdgeNode *p,*q;
	for(k=0;k<n;k++)
	{
		G[k].data=k+1;
		G[k].edge=NULL;//初始化建立n个顶点
	}

	for(k=0;k<e;k++)
	{
		scanf("%d %d %d",&vi,&vj,&weight);
		p=(EdgeNode*)malloc(sizeof(EdgeNode));//申请一个边节点
		p->adjvex=vj-1;
		p->weight=weight;
		p->link=NULL;
		if(!G[vi-1].edge)//若第vi个链表只有头结点
		{
			G[vi-1].edge=p;
		}
		else
		{
			q=G[vi-1].edge;
			while(q->link)
				q=q->link;//找到第vi个链表的尾节点
			q->link=p;//将新节点插入到第vi个链表表尾
		}
	}
}

3.图的遍历

#include  
#include
#include
#define MAX 200 
#define MaxValue 65535
bool visited[MAX];  //记录图中节点访问状态
typedef struct EdgeNode //边
{ 
	//边节点  
    int adjvex;    //该邻接点在顶点数组中的下标  
	int weight;
    struct EdgeNode *link;   //指向下一个邻接点  
}EdgeNode;

typedef struct ArrayNode 
{ 
    char data;  //顶点信息
    EdgeNode *edge;  //指向边节点
}ArrayNode,Arrays[MAX]; //顶点数组   

typedef struct Graph{  //图存放顶点和边
    Arrays arrays;  
    int numVertexes,numEdges;  //结点数以及边数  
}Graph,*GraphArrays;

3.1图的广度优先遍历

typedef struct LQueue
{
	int data[MAX];
	int front,rear;
}LQueue,*Queue; //创建循环队列

void init(Queue &Q)
{
	Q->front=Q->rear=0;
}
bool Empty(Queue &Q)
{
	if(Q->front==Q->rear)
	{
		return 1;
	}
	else
	{
		return 0;
	}
}
bool full(Queue &Q)
{
	if((Q->rear+1)%MAX==Q->front)
	{
		return 1;
	}
	else
	{
		return 0;
	}
}

void EnQueue(Queue &Q,int item)//对尾插入元素
{
	if(!full(Q))
	{
		Q->data[Q->rear]=item;
		Q->rear=(Q->rear+1)%MAX;
	}
}

void DeQueue(Queue &Q,int item)//对头删除元素
{
	if(!Empty(Q))
	{
		item=Q->data[Q->front];
		Q->front=(Q->front+1)%MAX;
	}
}
void BFS(GraphArrays &G)
{
	int i;
	//队列存储每一层的节点
	Queue Q=(Queue)malloc(sizeof(LQueue));
	for(i=0;i<G->numVertexes;i++)
	{
		visited[i]=0;
	}//初始化数组visited的元素值为0，表示均未访问
	init(Q);//初始化队列
	for(i=0;i<G->numVertexes;i++)
	{
		if(!visited[i])
		{
			visited[i]=1;
			printf("%d",G->arrays[i].data);
			//访问过的节点信息入队
			EnQueue(Q,i);
			while(!Empty(Q))
			{
				DeQueue(Q,i);
				EdgeNode *p = G->arrays[i].edge;
				while(p)
				{
					if(!visited[p->adjvex])
					{
						visited[p->adjvex]=1;
						printf("%d",G->arrays[p->adjvex].data);
						EnQueue(Q,p->adjvex);
					}
					p=p->link;
				}
			}
		}
	}
}

3.2图的深度优先遍历

void DFS(GraphArrays &G,int i)//从顶点i开始访问
{
	visited[i]=1;
	//输出访问的节点信息
	printf("%c",G->arrays[i].data);
	EdgeNode *p=G->arrays[i].edge;
	while(p)
	{
		if(!visited[p->adjvex])
		{
			DFS(G,p->adjvex);
		}
		p=p->link;//指向下一个节点
	}
}

void DFSTraverse(GraphArrays &G)
{
	int i;
	for(i=0;i<G->numVertexes;i++)
	{
		visited[i]=0;
	}//初始化数组visited的元素值为0，表示均未访问
	for(i=0;i<G->numVertexes;i++)
	{
		//节点未访问
		if(!visited[i])
			DFS(G,i);//递归访问
	}
}

4.图的拓扑排序

步骤
1.从AOV网中选择一个没有前驱的顶点（入度为0），输出它；
2.从AOV网中删去该顶点以及以它为弧尾的所有有向边；
3.重复上述两个步骤，直到剩余的网中不再存在没有前驱的顶点；

示意图：


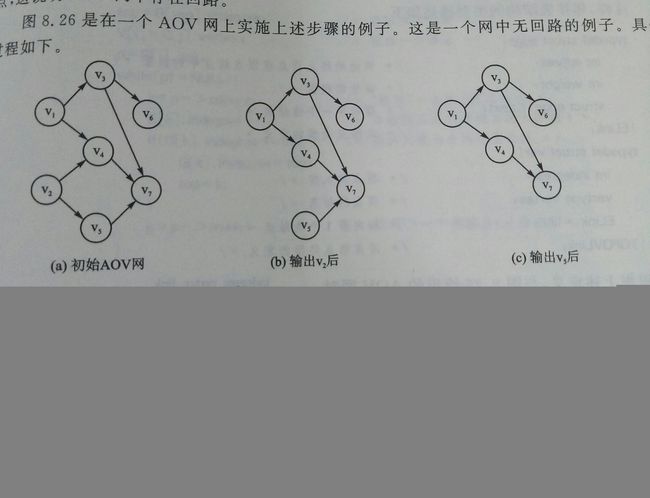
为了避免重复检测到入度为0的顶点，算法中将indegree域设置为一个链式结构的堆栈：栈中元素是通过顶点节点的下标进行链接的，凡是入度为0的顶点通过该链接栈连在一起。

拓扑排序步骤：
1.将所有入度为0的顶点压入栈
2.入栈不空，从栈中退出栈顶元素，并把该顶点引出的所有有向边删去，同时将该顶点指向的各个邻接点的顶点入度减1.
3.将新的入度为0的顶点压入堆栈
4.重复2和3，直到不再有入度为0的点。

#include
typedef struct edge
{
	int adjvex;//该边的终止节点在顶点节点中的位置
	struct edge *next;//指向下一个边节点
}ELink;

typedef struct ver
{
	int indegree;//顶点的入度
	char vertex;//顶点的信息
	ELink *link;//指向第一个边节点
}TLink;

void Topo_Sort(TLink G[],int n,char V[])
{
	ELink *p;
	int i,j,k;
	int top=-1;
	for(i=0;i<n;i++)//堆栈初始化
	{
		if(G[i].indegree==0)
		{
			G[i].indegree=top;
			top=i;
		}
	}
	for(i=0;i<n;i++)//拓扑排序
	{
		if(top==-1)
		{
			printf("存在回路!");
			break;
		}
		else
		{
			j=top; //j存放入读为0的顶点的下标
			top=G[top].indegree; //退出栈顶元素
			V[i]=G[j].vertex;//输出一个入度为0的顶点到V[i]数组中
			p=G[j].link;//p指向边节点
			while(p!=NULL)
			{
				k=p->adjvex;//删除一条由j发出的边
				G[k].indegree--; //当前输出点的邻接点的入度减一
				if(G[k].indegree==0) //将新的入度为0的顶点入栈
				{
					G[k].indegree=top;
					top=k;
				}
				p=p->next; //找到下一个邻接点
			}
		}
	}
}