数据降维——主成分分析PCA

一：预备知识
向量

向量的内积与投影：

两个向量A, B 内积的计算公式为：$A\blacksquare B=|A||B|cos(\alpha )$
1）向量内积的几何解释就是：向量A在向量B上的投影长度（$|A|cos(\alpha )$）乘以向量B的模
特别的，如果一个向量如a是某个坐标轴的单位向量，那么两个向量的内积$a\blacksquare b$就是向量在此坐标轴上的坐标值。
2）从内积的数值上我们可以看出两个向量在方向上的接近程度。当内积为正值时，两个向量大致指向相同的方向（方向夹角小于90度）；当内积为负值时，两个向量大致指向相反的方向；当内积值为0时，两个向量互相垂直。
（这个后面用于协方差和相关性的说明）

基与基变换：
1、定义：设$F^n的非空子集V是F上的向量空间，如果V中的(有序)向量组{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m线性表示满足$
（1）${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m线性无关；$
（2）$V中的向量都可由{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m线性表示,$

$那么，称向量组{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m是V的一个基.$

要准确的描述向量，首先要确定一组基（坐标轴，本质上也是一个向量），向量在各个坐标轴上的投影可以来定量的表示这个向量。

基变换的矩阵表示：

假设矩阵A的每一行代表一个向量空间的一个基，那么如果一个向量a在原来的向量空间其坐标值为$(a_1,a_2,a_3\dots \dots a_n)$,那么换算到新的向量空间后a的坐标值为：Aa 即：该向量a向矩阵A的每一行做投影。（此时暂时假设A的每一行都是单位向量）

可以看出基变换与矩阵内积是紧密相关的

注意上面的基变换操作变换前后向量a的维度是没有减少的，但是变换前后的向量空间的维度是不是可以不一致呢？（变换后的向量空间维度减少），这就是下面要讨论的数据降维问题。

方差与协方差：

首先在提到方差和协方差的时候，需要对其进一步区分：1）随机变量的方差和协方差 2）样本的方差和协方差
我们机器学习中一般都是指的样本的方差和协方差

样本均值：$\bar{x}=\frac{1}{n}\sum _{i=1}^N{x}_i$

样本方差：$S^2=\frac{1}{n-1}\sum _{i=1}^N(x_i-\bar{x}{)}^2$

样本X和样本Y的协方差：$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=\frac{1}{n-1}\sum _{i=1}^N(x_i-\bar{x})(y_i-\bar{y})$

上面这些都是从样本的角度出发的。

二 PCA基本概念理解

pca 主成分分析，其目的就是找到高维数据中的主成分，并利用"主成分"数据来表示原始数据，从而达到降维的目的。
（参考：https://www.jianshu.com/p/982c8f6760de）
借鉴一个简单的例子，假设有一组数据存在于三维空间的一个平面上（此时需要3个维度来表征数据向量），若我们选择旋转坐标轴使得数据所在平面与x,y平面重合，则此时我们只需要2个纬度即可表征数据，且没有丢失任何数据信息，这就是最简单的数据降维

但是现实生活中的情况，往往数据特征高达上百甚至上千维，我们很难直观去找出一组基平面来完成对数据的降维，此时PCA就有其用武之地了

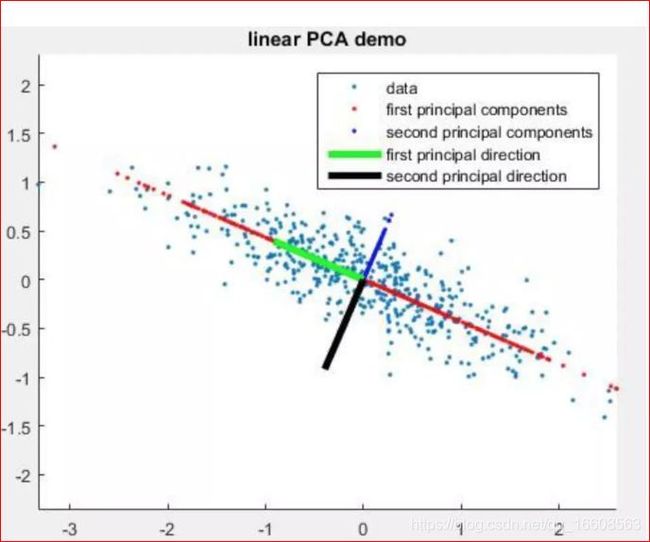
如图可见，绿色线为第一主成成分方向，黑色线为第二主成成分方向。仔细观察一下图，大家是否能得出如下俩个结论：

（1） 样本点在绿色线上的投影其离散程度要大于其在黑色线上的投影程度。
（2） 样本点到绿色线的平均距离都要小于其到黑色线的距离。

西瓜书上将此俩个结论归纳为最大可分析和最近重构性。其中最大可分性可以理解为我们希望降维过后的数据不影响后续我们对其的分类处理，其数据特征的差异性仍然足够强，也即方差最大；最近重构性可以理解为我们希望降维过后的数据仍然保留有其主要的特征，也即数据样本点到这个超平面的距离和最小。

PCA推导之最大可分性：

最大可分性理论的目标函数就是最大化数据在主轴上的投影的方差。（最大化方差）

假设现有一组已去中心化的数据$\{x_1,x_2,x_3\dots \dots x_n\}$,其中向量$x_i$在W超平面上的投影为：$x_{i}W$,那么投影后的方差可以表示为：
$D(x)=\frac{1}{n}\sum _{i=1}^n(x_i^{T}W{)}^2$

展开以后，我们可以得到$D(x)=\frac{1}{n}\sum _{i=1}^n{W}^T{x}_i{x}_i^{T}W$
样本的协方差矩阵为：$C=\sum _{i=1}^n{x}_i{x}_i^T=X{X}^T$

而$D(x)$就是降维后的样本的协方差矩阵。我们的优化目标就是同一维度的方差最大，不同维度的相关性为0
理想的协方差矩阵为：

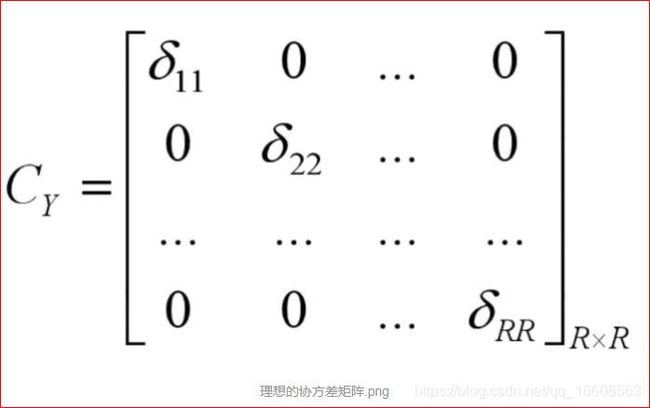
如果我们期望同一维度的方差最大，本质上就等于最大化该降维后样本的协方差矩阵的迹

优化目标便成了：
$maxtr(W^{T}CW)$
$s.t.W^{T}W=I$
引入拉格朗日乘子得到：
$f(W)=tr(W^{T}CW)+\lambda (W^{T}W-I)$ 求导令其等于0

$\frac{\partial f}{\partial W}=\frac{\partial tr(W^{T}CW)}{\partial W}+\lambda \frac{\partial (W^{T}W)}{\partial W}=0$

推出：$CW=\lambda W$ 此时$D(x)=W^{T}CW=W^T\lambda W=\lambda$
（推导没咋搞明白，抄过来的，记住下面的总结就可以了，哎数学学得不好硬伤）

总结：原来x投影后的方差就是协方差矩阵的特征值，而我们想要的最大方差，显然就是协方差矩阵最大的特征值，最佳投影方向就是最大特征值对应的特征向量。

特征值与特征向量与矩阵的特征值分解：

矩阵乘法一种物理解释为：两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。

一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为B中第m列列变换后结果。

特征值和特征向量表达了一个线性变换的特征。在物理意义上，一个高维空间的线性变换可以想象是在对一个向量在各个方向上进行了不同程度的变换，而特征向量之间是线性无关的，它们对应了最主要的变换方向，同时特征值表达了相应的变换程度。

如果一个向量v是矩阵A的特征向量，将一定可以表示成下面的形式：$Av=\lambda v$
看见没特征向量只是拉伸了，而没有扭曲，计算简单。

PCA算法的两种实现：
1）基于特征值分解协方差矩阵实现PCA算法

2）基于SVD分解协方差矩阵实现PCA算法

在PCA降维中，我们需要找到样本协方差矩阵的最大k个特征向量，然后用这最大的k个特征向量组成的矩阵来做低维投影降维

这两种实现方法进行比较：

特征值分解的局限性：1）首先要求协方差矩阵是个可对角化的方阵 2）当样本数目多，且样本特征数也多的时候，求协方差矩阵计算量太大。

奇异值分解优点：1）奇异值分解是一个能适用于任意矩阵的一种分解的方法，对于任意矩阵A总是存在一个奇异值分解2）有一些SVD的实现算法可以先不求出协方差矩阵也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解而是通过SVD来完成，这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是特征值分解

如何选择降维后的维度K(主成分个数)：

主要是从数据有多大程度的失真考虑的：

三 、LDA的基本概念理解：

LDA中文名为 ”线性判别分析“，从降维的层面考虑，其也是在寻找一个投影矩阵，使得投影之后的数据样本，同类的接近，而不同类的远离。

其作为分类器的时候，就可以对新的数据也进行投影，依据与哪一个类别接近来确定类别。

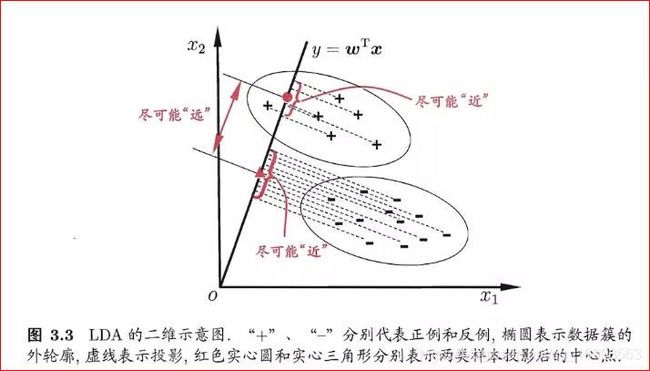
LDA的原理是，将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近，不同类别的点应该尽可能的远离。

LDA的中心思想就是最大化类间距离以及最小化类内距离。其推导过程也是按照这个思想来的

假设是用来进行二分类的直线（投影函数）为：$y=w^{T}x$

LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好，所以我们定义几个关键的值。

1）类别i的原始中心点为：（$D_i表示属于类别i的点$）$m_i=\frac{1}{n_i}\sum _{x\in D_i}x$
类别投影后的中心点为：${\bar{m}}_i=w^T{m}_i$

2)衡量类别i投影后，类别点之间的分散程度（方差）为：
${\bar{s}}_i=\sum _{y\in Y_i}(y-{\bar{m}}_i{)}^2$

最终我们可以得到一个下面的公式，表示LDA投影到w后的损失函数：

$J(w)=\frac{|{\bar{m}}_1-{\bar{m}}_2{|}^2}{{\bar{s}}_1+{\bar{s}}_2}$

我们分类的目标是，使得类别内的点越近越好（集中），类别间的点越远越好。
1）分母表示每一个类别内的方差之和，方差越大表示一个类别内的点越分散（我们希望上式中分母越小越好）
2）分子为两个类别各自的中心点的距离的平方，表示类别间离得有多远，我们希望这个值越大越好

总结以上两点，我们要求$J(w)$的最大值。

定义类内散度矩阵$S_i=\sum _{x\in D_i}(x-m_i)(x-m_i{)}^T$

类内散度的意义是：如果一个类$D_i$里面的点距离这个分类的中心点$m_i$越近，则$S_i$里面的元素的值就越小，如果分类的点都仅仅围绕着$m_i$,则$S_i$里面的元素的值越接近于0

带入$S_i则J(w)的分母化为$：
${\bar{s}}_i=\sum _{x\in D_i}(w^{T}x-w^T{m}_i{)}^2=\sum _{x\in D_i}{w}^T(x-m_i)(x-m_i{)}^{T}w=w^T{S}_{i}w$

${\bar{s}}_1+{\bar{s}}_2=w^T(S_1+S_2)w=w^T{S}_{w}w$
同样，将$J(w)的分子化为：|{\bar{m}}_1-{\bar{m}}_2{|}^2=w^T(m_1-m_2)(m_1-m_2{)}^{T}w=w^T{S}_{B}w$
其中$S_B定义为$类间散度矩阵

这样损失函数可以化成下面的形式：

$J(w)=\frac{w^T{S}_{B}w}{w^T{S}_{w}w}$

上式对$w求导，令其为零得到S_{B}w=\lambda S_{w}w即：S_w^{-1}{S}_{B}w=\lambda w$

到此可以看出来$w是矩阵S_w^{-1}{S}_B关于特征值\lambda 的特征向量$

对于多分类的情况知道结论就行，思想都一样 类间尽可能远，类内尽可能近

LDA用于降低维度：

LDA与PCA的比较：
1）PCA为非监督降维，LDA为有监督降维
2）PCA希望投影后的数据方差尽可能的大（最大可分性），因为其假设方差越多，则所包含的信息越多；而LDA则希望投影后相同类别的组内方差小，而组间方差大。LDA能合理运用标签信息，使得投影后的维度具有判别性，不同类别的数据尽可能的分开

参考：https://www.jianshu.com/p/982c8f6760de
https://blog.csdn.net/c_dreams/article/details/78460741