深度学习笔记(13.numpy实现LSTM)

摘要

Ng深度学习课程第五部分序列化模型，第一周作业numpy实现，并利用LSTM生成恐龙名称实验。涉及到正向传播、反向传播公式，程序的整合，部分理论学习。代码注释添加了部分说明。和RNN程序流程基本一样，部分代码流程做了优化。实验程序用于检验程序是否正确，loss逐步下降，名称越来越像。
程序地址：https://github.com/ConstellationBJUT/Coursera-DL-Study-Notes

代码结构

dinos.txt：数据文件，每行是一个恐龙名称
lstm.py：numpy实现的lstm模型
lstm_dinasaurus_name.py：lstm生成恐龙名字程序

程序查看顺序：
(1)lstm_dinosaurus_name.py的model()：实验入口程序，完成数据变换，将名称转换为rnn认识的数据格式。
(2)lstm.py的optimize：lstm正向传播、损失计算、反向传播、参数更新。
(3)lstm_dinosaurus_name.py的sample()：根据模型计算得到的参数，按概率生成字符，字符拼接成名字

LSTM网络结构

比RNN多了ci，其它如输入X和输出Y与上一篇RNN保持一致，具体参考如下https://blog.csdn.net/bjjoy2009/article/details/103506065

cell结构

正向传播，实现下图的公式。中间圈符号表示矩阵按照位置乘，[a,x]表示将矩阵a和x拼接，例如a.shape=(n_a, 1)，x.shape=(n_x, 1)，[a, x].shape=(n_a + n_x, 1)

LSTM算法和程序

1.正向传播

（1） lstm_forward()，用于接收输入数据、初始化参数，调用lstm_cell_forward()来时先每个cell的计算。

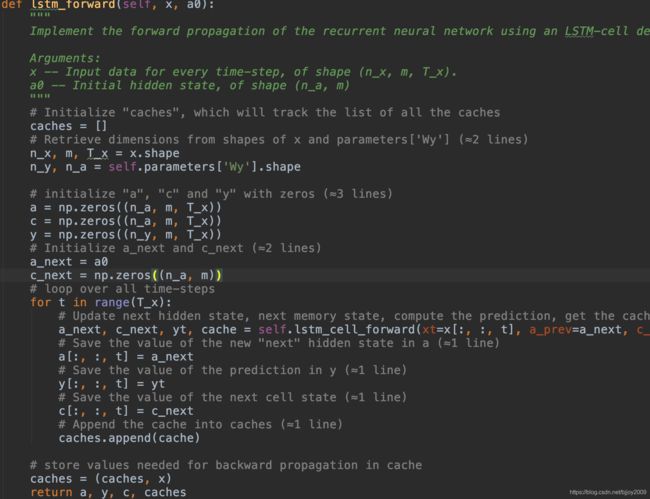
（2）lstm_cell_forward()，绿色框对应的6个公式，concat对应[a, x]。it对应公式第二个(${\Gamma }_u^{<t>}$)，cct对应公式第三个${\hat{c}}^{<t>}$

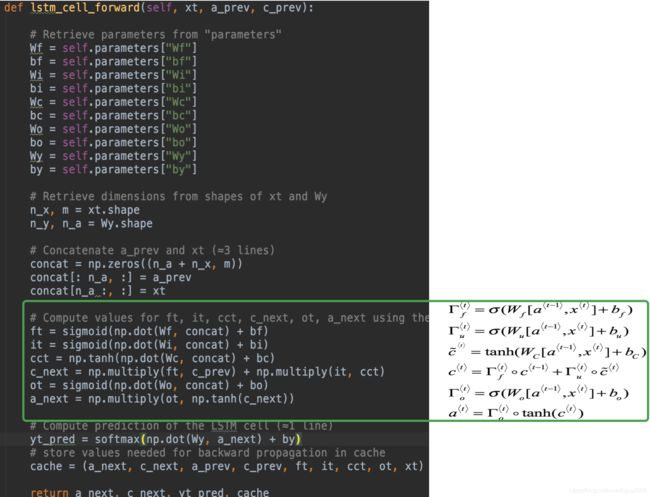
2. loss计算

就是softmax交叉熵损失函数，每个cell的损失求和，有m个样本就除以m。

def compute_loss(self, y_hat, y):
    """
     计算损失函数
     :param y_hat: (n_y, m, T_x),经过rnn正向传播得到的值
     :param y: (n_y, m, T_x),标记的真实值
     :return: loss
     """
     n_y, m, T_x = y.shape
     for t in range(T_x):
         self.loss -= 1/m * np.sum(np.multiply(y[:, :, t], np.log(y_hat[:, :, t])))
     return self.loss

3. 反向传播

（1）lstm_backward，初始化每次反向传播参数，然后调用lstm_cell_backward
注意：
i) dz=y_hat - y，是softmax(z)对z求导公式。
ii) for循环调用lstm_cell_backward，计算序列每个时刻cell反向传播，并对序列中每个cell中对应参数变化量gradients求和，gradients[‘da_next’]和gradients[‘dc_next’]是前一时刻cell的反向传播的输入。

def lstm_backward(self, y, y_hat, caches):

        """
        Implement the backward pass for the RNN with LSTM-cell (over a whole sequence).

        Arguments:
        :param y: one_hot label, shape (n_y, m, T_x)
        :param y_hat: lstm_forward 计算结果, shape (n_y, m, T_x)
        caches -- cache storing information from the forward pass (lstm_forward)

        Returns:
        gradients -- python dictionary containing:
                dx -- Gradient of inputs, of shape (n_x, m, T_x)
                da0 -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
                dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
                dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
                dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x)
                dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
                dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
                dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
                dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1)
                dWy -- Gradient w.r.t. the weight matrix of output, numpy array of shape (n_y, n_a)
                dby -- Gradient w.r.t. biases of output, numpy array of shape (n_y, 1)
        """

        # Retrieve values from the first cache (t=1) of caches.
        (caches, x) = caches

        # Retrieve dimensions from da's and x1's shapes (≈2 lines)
        n_x, m, T_x = x.shape
        n_a = self.n_a
        # initialize the gradients with the right sizes (≈12 lines)
        dx = np.zeros((n_x, m, T_x))
        da0 = np.zeros((n_a, m))
        da_next = np.zeros((n_a, m))
        dc_next = np.zeros((n_a, m))
        dWf = np.zeros((n_a, n_a + n_x))
        dWi = np.zeros((n_a, n_a + n_x))
        dWc = np.zeros((n_a, n_a + n_x))
        dWo = np.zeros((n_a, n_a + n_x))
        dWy = np.zeros((self.n_y, n_a))
        dbf = np.zeros((n_a, 1))
        dbi = np.zeros((n_a, 1))
        dbc = np.zeros((n_a, 1))
        dbo = np.zeros((n_a, 1))
        dby = np.zeros((self.n_y, 1))
        dz = y_hat - y  # y_hat=softmax(z), dz=dl/dy_hat * dy_hat/dz

        # loop back over the whole sequence
        for t in reversed(range(T_x)):
            # Compute all gradients using lstm_cell_backward
            gradients = self.lstm_cell_backward(dz=dz[:, :, t], da_next=da_next, dc_next=dc_next, cache=caches[t])
            # Store or add the gradient to the parameters' previous step's gradient
            dx[:, :, t] = gradients["dxt"]
            dWf = dWf+gradients["dWf"]
            dWi = dWi+gradients["dWi"]
            dWc = dWc+gradients["dWc"]
            dWo = dWo+gradients["dWo"]
            dWy = dWy+gradients["dWy"]
            dbf = dbf+gradients["dbf"]
            dbi = dbi+gradients["dbi"]
            dbc = dbc+gradients["dbc"]
            dbo = dbo+gradients["dbo"]
            dby = dby+gradients["dby"]
            da_next = gradients['da_next']
            dc_next = gradients['dc_next']

        # Set the first activation's gradient to the backpropagated gradient da_prev.
        da0 = gradients['da_next']

        gradients = {"dx": dx, "da0": da0, "dWf": dWf, "dbf": dbf, "dWi": dWi, "dbi": dbi,
                     "dWc": dWc, "dbc": dbc, "dWo": dWo, "dbo": dbo, "dWy": dWy, "dby": dby}

        return gradients

（2）lstm_cell_backward，计算t时刻cell反向传播，公式太长，先贴出公式图片。
红色框程序实现时候出现了点问题，*符号乘法应该替换为np.dot。
说明：np.dot表示矩阵乘法，np.multiply表示矩阵按位置乘。*做乘法有2种情况，如果是np.mat数据格式表示矩阵乘法（相当于np.dot），如果是np.array数据格式表示按位置乘（相当于np.multiply）

程序流程，先计算dWy和dby，da（2部分组成，输出da和da_naxt），然后按照上图公式列出来。

def lstm_cell_backward(self, dz, da_next, dc_next, cache):
        """
        Implement the backward pass for the LSTM-cell (single time-step).

        Arguments:
        dz -- cell输出y_hat=softmax(z)对z求导
        da_next -- Gradients of next hidden state, of shape (n_a, m)
        dc_next -- Gradients of next cell state, of shape (n_a, m)
        cache -- cache storing information from the forward pass
        """

        # Retrieve information from "cache"
        (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt) = cache

        # Retrieve dimensions from xt's and a_next's shape (≈2 lines)
        n_a, m = a_next.shape

        dWy = np.dot(dz, a_next.T)
        dby = np.sum(dz, axis=1, keepdims=True)
        # cell的da由两部分组成
        da_next = np.dot(self.parameters['Wy'].T, dz) + da_next

        # Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
        dot = da_next * np.tanh(c_next) * ot * (1 - ot)
        dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
        dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
        dft = (dc_next * c_prev + ot * (1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)

        # Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
        concat = np.vstack((a_prev, xt)).T
        dWf = np.dot(dft, concat)
        dWi = np.dot(dit, concat)
        dWc = np.dot(dcct, concat)
        dWo = np.dot(dot, concat)
        dbf = np.sum(dft, axis=1, keepdims=True)
        dbi = np.sum(dit, axis=1, keepdims=True)
        dbc = np.sum(dcct, axis=1, keepdims=True)
        dbo = np.sum(dot, axis=1, keepdims=True)

        # Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
        da_prev = np.dot(self.parameters['Wf'][:, :n_a].T, dft) + np.dot(self.parameters['Wi'][:, :n_a].T, dit) + np.dot(self.parameters['Wc'][:, :n_a].T, dcct) + np.dot(self.parameters['Wo'][:, :n_a].T, dot)
        dc_prev = dc_next * ft + ot * (1 - np.square(np.tanh(c_next))) * ft * da_next
        dxt = np.dot(self.parameters['Wf'][:, n_a:].T, dft) + np.dot(self.parameters['Wi'][:, n_a:].T, dit) + np.dot(self.parameters['Wc'][:, n_a:].T, dcct) + np.dot(self.parameters['Wo'][:, n_a:].T, dot)

        # Save gradients in dictionary
        gradients = {"dxt": dxt, "da_next": da_prev, "dc_next": dc_prev, "dWf": dWf, "dbf": dbf, "dWi": dWi, "dbi": dbi,
                     "dWc": dWc, "dbc": dbc, "dWo": dWo, "dbo": dbo, "dWy": dWy, "dby": dby}

        return gradients

4.梯度算法更新参数

self.alpha = learning_rate

def update_parameters(self, gradients):
    """
     梯度下降
     :param gradients:
     :return:
     """
     self.parameters['Wf'] += -self.alpha * gradients["dWf"]
     self.parameters['Wi'] += -self.alpha * gradients["dWi"]
     self.parameters['Wc'] += -self.alpha * gradients['dWc']
     self.parameters['Wo'] += -self.alpha * gradients["dWo"]
     self.parameters['Wy'] += -self.alpha * gradients['dWy']

     self.parameters['bf'] += -self.alpha * gradients['dbf']
     self.parameters['bi'] += -self.alpha * gradients['dbi']
     self.parameters['bc'] += -self.alpha * gradients['dbc']
     self.parameters['bo'] += -self.alpha * gradients['dbo']
     self.parameters['by'] += -self.alpha * gradients['dby']

实验结果

实验生成字符程序在sample()函数中，就是生成一个字符(输出y)的one_hot向量，作为下一个cell的输入x，直到生成字符\n或者生成了50个字符结束。
Iteration: 6000, Loss: 26.024013

Khvsrolonos
Hiecalosaurus
Hwtosaurus
Kecalosaurus
Xtppeonos
Caalosaurus
Usnanerontisaurus

Iteration: 8000, Loss: 24.694760

Jhytrognesaurus
Hicabdosaurus
Hytrognesaurus
Jacakton
Ytroeomor
Caagtona
Usodonnonus

总结

（1）单纯的实现了LSTM的基本流程，感觉和RNN流程没有啥差别，有了RNN实现的基础，感觉LSTM实现也容易多了。
（2）没有推导反向传播公式，感觉的确推导挺难的，需要根据cell那个图确定每个参数变化由哪些参数变化确定，再进行加和。
（3）第三点还有啥呢？凑一下吧，还是得用keras或者tensorflow做做，感觉用框架也不是啥容易事。