【三维重建】三维重建学习笔记（4）—— 三维重建基础与极几何
第四章 三维重建基础与极几何
一、三维重建基础
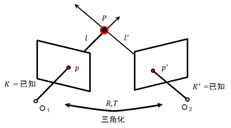
1. 三角化模型
三角化模型
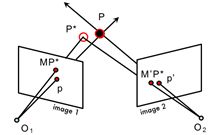
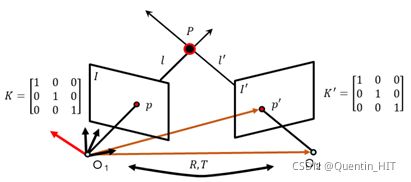
在理想情况下，\(P=l\times {l}'\)。但是由于噪声的存在，两条直线通常不相交，因此就存在新的问题：已知\(p\)和\({p}'\)，\(K\)和\({K}'\)以及\(R\)和\(T\)，如何求解\(P\)的三维坐标？（可通过线性解法和非线性解法求解）
最优化求解模型
寻找\({{P}^{*}}\)，使得\(d(p,M{{P}^{*}})+d({p}',{M}'{{P}^{*}})\)最小化。具体可使用牛顿法或列文伯格-马夸尔特法（L-M方法）。
2. 多视图几何的关键问题
- 摄像机几何：从一张或多张图像中求解摄像机的内、外参数（第二章解决）
- 场景几何：通过二张或多幅图寻找3D场景坐标（以上解决）
- 对应关系：已知一个图像中的\(p\)点，如何在另外一个图像中找到\({p}'\)点（以下解决）
二、极几何
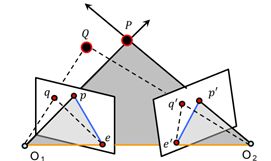
1. 极几何的概念
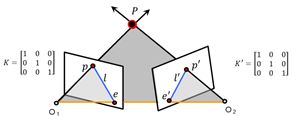
极几何描述了同一场景或者物体的两个视点图像间的几何关系。
极几何示意图
定义：
- 极平面：过点\(P\)，\({{O}_{1}}\)与\({{O}_{2}}\)的平面，图中灰色平面
- 基线：\({{O}_{1}}\)与\({{O}_{2}}\)的连线，图中橙色直线
- 极线：极平面与成像平面的交线，图中蓝色直线
- 极点：基线与成像平面的交点，图中\(e\)和\({e}'\)点
性质：
- 极平面相交于基线
- 极线相交于极点
- \(p\)的对应点在极线\({l}'\)上
- \({p}'\)的对应点在极线\(l\)上
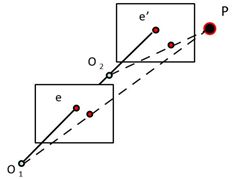
2. 极几何特例1：平行视图
极几何特例：平行视图
两个图像平面平行
基线平行于图像平面，极点\(e\)和\({e}'\)位于无穷远处
极线平行于图像坐标系的\(u\)轴
3. 极几何特例2：前向平移（无旋转）
极几何特例：前向平移
两幅图上极点的位置相同，极点称作展开焦点。
4. 极几何约束
极几何约束
通过极几何约束，可以将搜索范围缩小到对应的极线上。
三、本质矩阵
1. 本质矩阵的概念
本质矩阵对规范化摄像机拍摄的两个视点图像间的极几何关系进行代数描述。
回顾：规范化摄像机满足\(K=\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\\end{matrix} \right]\)。
2. 数学知识
定义：\(a\times b=\left[ \begin{matrix} 0 & -{{a}_{z}} & {{a}_{y}} \\ {{a}_{z}} & 0 & -{{a}_{x}} \\ -{{a}_{y}} & {{a}_{x}} & 0 \\\end{matrix} \right]\left[ \begin{matrix} {{b}_{x}} \\ {{b}_{y}} \\ {{b}_{z}} \\\end{matrix} \right]=[{{a}_{\times }}]b\)
注意：
- 这里\([{{a}_{\times }}]\)是不满秩的，秩=2<3
- \([{{a}_{\times }}]\)是反对称矩阵，转置矩阵和原矩阵差一个负号
3. 本质矩阵的推导
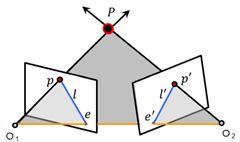
设两个相机均为规范相机，因此：图像点的齐次坐标=空间点的欧式坐标。
因此空间点\(p\)在\({{O}_{1}}\)坐标系下的非齐次坐标为\({{[u,v,1]}^{T}}\)，空间点\({p}'\)在\({{O}_{2}}\)坐标系下的非齐次坐标为\({{[{u}',{v}',1]}^{T}}\)。
本质矩阵
\({p}'\)在\({{O}_{1}}\)的坐标：\({{R}^{T}}{p}'-{{R}^{T}}T\)
\({{O}_{2}}\)在\({{O}_{1}}\)的坐标：\(-{{R}^{T}}T\)
由此可以推出上图红色向量（垂直于极平面）\({{R}^{T}}T\times ({{R}^{T}}{p}'-{{R}^{T}}T)\)
该向量垂直于\({{O}_{1}}p\)，因此\({{[{{R}^{T}}T\times ({{R}^{T}}{p}'-{{R}^{T}}T)]}^{T}}p=0\)，化简可得：\[{{{p}'}^{T}}[T\times R]p={{{p}'}^{T}}[{{T}_{\times }}]Rp=0\]
定义本质矩阵\(E=T\times R=[{{T}_{\times }}]R\)，即可得到：\[{{{p}'}^{T}}Ep=0\]
极几何示意图
结论：
- \(p\)对应的极线是\({l}'\)，并且\({l}'=Ep\)
- \({p}'\)对应的极线是\(l\)，并且\(l={{E}^{T}}{p}'\)
- \(Ee=0\)
- \({{E}^{T}}{e}'=0\)
- \(E\)是奇异阵，秩为2
- \(E\)有5个自由度（3平移+3旋转，行列式为0去掉一个自由度）
四、基础矩阵
1. 基础矩阵的概念
基础矩阵对一般的透视摄像机拍摄的两个视点的图像间的极几何关系进行代数描述。
思路：变换到规范化摄像机
2. 基础矩阵的推导
由于\(p=K\left[ \begin{matrix} I & 0 \\\end{matrix} \right]P\)，因此\({{K}^{-1}}p={{K}^{-1}}K\left[ \begin{matrix} I & 0 \\\end{matrix} \right]P=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\\end{matrix} \right]P\)
故可令\({{p}_{c}}={{K}^{-1}}p\)，\({{p}_{c}}^{\prime }={{{K}'}^{-1}}{p}'\)
因此：\[{{p}_{c}}^{\prime }E{{p}_{c}}={{p}_{c}}^{\prime }[{{T}_{\times }}]R{{p}_{c}}={{{p}'}^{T}}{{{K}'}^{-T}}[{{T}_{\times }}]R{{K}^{-1}}p=0\]
定义基础矩阵\(F={{{K}'}^{-T}}[{{T}_{\times }}]R{{K}^{-1}}\)，即可得到：\[{{{p}'}^{T}}Fp=0\]
极几何示意图
结论：
- \(p\)对应的极线是\({l}'\)，并且\({l}'=Fp\)
- \({p}'\)对应的极线是\(l\)，并且\(l={{F}^{T}}{p}'\)
- \(Fe=0\)
- \({{F}^{T}}{e}'=0\)
- \(F\)是奇异阵，秩为2
- \(F\)有7个自由度（3行3列，尺度无法确定，行列式为0各去掉一个自由度）
3. 基础矩阵的作用及小结
- 作用：已知\(F\)，无需场景信息以及摄像机内、外参数，即可建立左右图像对应关系
- \(F\)刻画了两幅图像的极几何关系，即相同场景在不同视图中的对应关系
- \(F\)应包含摄像机内参数信息
- 基础矩阵可应用于三维重构和多视图匹配
五、基础矩阵估计
1. 八点算法
\(F\)有7个自由度，理论上7个点即可求解\(F\)，但是计算方法比较复杂。故使用八点算法来估计\(F\)。
根据\({{{p}'}^{T}}Fp=0\)，可以得到：\(\left[ \begin{matrix} {{u}'} & {{v}'} & 1 \\\end{matrix} \right]\left[ \begin{matrix} {{F}_{11}} & {{F}_{12}} & {{F}_{13}} \\ {{F}_{21}} & {{F}_{22}} & {{F}_{23}} \\ {{F}_{31}} & {{F}_{32}} & {{F}_{33}} \\\end{matrix} \right]\left[ \begin{matrix} u \\ v \\ 1 \\\end{matrix} \right]=0\)，即：\[\left[ \begin{matrix} u{u}' & v{u}' & {{u}'} & u{v}' & v{v}' & {{v}'} & u & v & 1 \\\end{matrix} \right]\left[ \begin{matrix} {{F}_{11}} \\ {{F}_{12}} \\ {{F}_{13}} \\ {{F}_{21}} \\ {{F}_{22}} \\ {{F}_{23}} \\ {{F}_{31}} \\ {{F}_{32}} \\ {{F}_{33}} \\\end{matrix} \right]=0\]
选取八组对应点：\[\left[ \begin{matrix} {{u}_{1}}{{{{u}'}}_{1}} & {{v}_{1}}{{{{u}'}}_{1}} & {{{{u}'}}_{1}} & {{u}_{1}}{{{{v}'}}_{1}} & {{v}_{1}}{{{{v}'}}_{1}} & {{{{v}'}}_{1}} & {{u}_{1}} & {{v}_{1}} & 1 \\ {{u}_{2}}{{{{u}'}}_{2}} & {{v}_{2}}{{{{u}'}}_{2}} & {{{{u}'}}_{2}} & {{u}_{2}}{{{{v}'}}_{2}} & {{v}_{2}}{{{{v}'}}_{2}} & {{{{v}'}}_{2}} & {{u}_{2}} & {{v}_{2}} & 1 \\ {{u}_{3}}{{{{u}'}}_{3}} & {{v}_{3}}{{{{u}'}}_{3}} & {{{{u}'}}_{3}} & {{u}_{3}}{{{{v}'}}_{3}} & {{v}_{3}}{{{{v}'}}_{3}} & {{{{v}'}}_{3}} & {{u}_{3}} & {{v}_{3}} & 1 \\ {{u}_{4}}{{{{u}'}}_{4}} & {{v}_{4}}{{{{u}'}}_{4}} & {{{{u}'}}_{4}} & {{u}_{4}}{{{{v}'}}_{4}} & {{v}_{4}}{{{{v}'}}_{4}} & {{{{v}'}}_{4}} & {{u}_{4}} & {{v}_{4}} & 1 \\ {{u}_{5}}{{{{u}'}}_{5}} & {{v}_{5}}{{{{u}'}}_{5}} & {{{{u}'}}_{5}} & {{u}_{5}}{{{{v}'}}_{5}} & {{v}_{5}}{{{{v}'}}_{5}} & {{{{v}'}}_{5}} & {{u}_{5}} & {{v}_{5}} & 1 \\ {{u}_{6}}{{{{u}'}}_{6}} & {{v}_{6}}{{{{u}'}}_{6}} & {{{{u}'}}_{6}} & {{u}_{6}}{{{{v}'}}_{6}} & {{v}_{6}}{{{{v}'}}_{6}} & {{{{v}'}}_{6}} & {{u}_{6}} & {{v}_{6}} & 1 \\ {{u}_{7}}{{{{u}'}}_{7}} & {{v}_{7}}{{{{u}'}}_{7}} & {{{{u}'}}_{7}} & {{u}_{7}}{{{{v}'}}_{7}} & {{v}_{7}}{{{{v}'}}_{7}} & {{{{v}'}}_{7}} & {{u}_{7}} & {{v}_{7}} & 1 \\ {{u}_{8}}{{{{u}'}}_{8}} & {{v}_{8}}{{{{u}'}}_{8}} & {{{{u}'}}_{8}} & {{u}_{8}}{{{{v}'}}_{8}} & {{v}_{8}}{{{{v}'}}_{8}} & {{{{v}'}}_{8}} & {{u}_{8}} & {{v}_{8}} & 1 \\\end{matrix} \right]\left[ \begin{matrix} {{F}_{11}} \\ {{F}_{12}} \\ {{F}_{13}} \\ {{F}_{21}} \\ {{F}_{22}} \\ {{F}_{23}} \\ {{F}_{31}} \\ {{F}_{32}} \\ {{F}_{33}} \\\end{matrix} \right]=0\]
方程记为\(\mathbf{Wf}\text{=}0\)，该方程秩为8，存在唯一非零解。
实际操作中可能多于8组数据，需要用最优化的方法来求出\(\hat{F}\)。这个\(\hat{F}\)是满秩的，而我们所要求的\(F\)秩为2，故仍需要使用最优化方法求出\(F\)。
\[SVD(\hat{F})=U\left[ \begin{matrix} {{s}_{1}} & 0 & 0 \\ 0 & {{s}_{2}} & 0 \\ 0 & 0 & {{s}_{3}} \\\end{matrix} \right]{{V}^{T}}\Rightarrow F=U\left[ \begin{matrix} {{s}_{1}} & 0 & 0 \\ 0 & {{s}_{2}} & 0 \\ 0 & 0 & {{s}_{3}} \\\end{matrix} \right]{{V}^{T}}\]
2. 归一化八点法
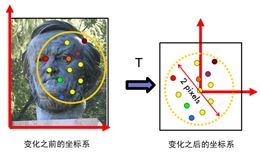
由于\(\mathbf{W}\)矩阵中各个元素的数值差异过大，SVD分解有数值计算问题，因此引入归一化八点法。
对每幅图像施加变换T（平移与缩放），让其满足如下条件：
- 原点=图像上点的重心
- 各个像点到坐标原点的均方根距离等于\(\sqrt{2}\)
归一化实例
具体步骤如下：
- 分别计算左图和右图的\(T\)和\({T}'\)
- 坐标归一化：\({{q}_{i}}=T{{p}_{i}}\) \({{{q}'}_{i}}={T}'{{p}_{i}}^{\prime }\)
- 通过八点法计算矩阵\({{F}_{q}}\)
- 逆归一化：\(F={{{T}'}^{T}}{{F}_{q}}T\)