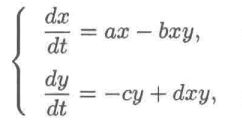捕食者-被捕食者方程组分析

捕食者-被捕食者方程组研究

《python数学实验与建模》中课后习题与代码解读2。

捕食者与被捕食者属于经典生态动力学问题，本次建模问题也是传统模型，并没有进行扩展。

一、问题描述

        假设封闭草原环境下，以兔子x(t)和狐狸y(t)的数量变化作为基本研究对象，x(0)=60,y(0)=60，并且假设只有这两种生物相互影响，没有其它外界影响。通过为期一定时间的观察，兔子与狐狸的基本观测值如下表所示：

        并且已知基本传统模型如下所示，要求根据观测值拟合求出a,b,c,d的值。

二、问题求解

        微分模型对于连续型数据具有意义，但是通过给出的表格数据，可以看出观测值属于离散量。所以可以将微分方程改为差分方程的形式。最终可将方程改写为Ax=b的形式（具体解析可查看司守奎老师的《python数学建模算法与应用》一书）。

求解过程python实现如下所示：

#利用线性最小二乘方法，估算整体的最小值
import numpy as np
t0 = np.array([0,1,2,3,4,5,6,8,10,12,14,16,18])
x0 = np.array([60,63,64,63,61,58,53,44,39,38,41,46,53])
y0= np.array([30,34,38,44,50,55,58,56,47,38,30,27,26])
dt = np.diff(t0)#输出t方向的离散差值
dx = np.diff(x0)#输出x轴方向的离散差值
dy = np.diff(y0)#输出y轴方向的离散差值
temp = x0[:-1]*y0[:-1]#x与y的乘积
mat1 = np.vstack([x0[:-1],-temp,np.zeros((2,12))]).T#按照列方向堆叠
print(mat1)
mat2 = np.vstack([np.zeros((2,12)),-y0[:-1],temp]).T#按照列方向堆叠
print(mat2)
mat = np.vstack([mat1,mat2])#构造线性方程组的系数矩阵
print(mat)#堆叠形成左边的矩阵
b = np.hstack([dx/dt,dy/dt])#按照行方向堆叠，构造线性方程组的常数项列
print(b)
cs = (np.linalg.pinv(mat))@b
''''
利用pinv函数求解mat的伪逆矩阵，
奇异矩阵和非方阵没有逆矩阵，但是可以有伪逆矩阵
''''
print('参数a,b,c,d为：',np.round(cs,5))#给cs保留5位小数

        需要注意求解过程中，A为不可逆矩阵，所以为了求方程的解，只能使用伪逆矩阵，来达到最小线性二乘拟合。如果不理解，可以尝试多使用print输出查看实现效果，最终求解出的结果如图下所示：

参数a,b,c,d为： [0.19074 0.00483 0.48289 0.00954]

三、模型分析

        上述工作主要是为了求解出参数，并没有做图像分析。

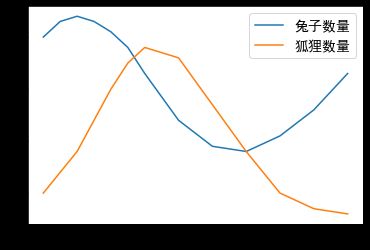
        将上述表格数据直接画折线图输出如下所示，图形展示短期的波动变化。由图可见兔子的数量有增有减，但是狐狸的数量经历了增加到减少之后便没有上升的趋势，常识告诉我们狐狸的数量并非会如此停滞。所以需要进一步的分析。

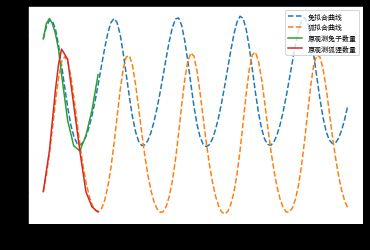
        我们利用题目给出的初值，以及求解出的模型参数进行模型的拟合（此处与原给出的数据无关），和原观测值做出图像如下所示：

        从上图可以看出，整体的拟合效果还不错，但是依然还是不够理想，还是有误差，可以进一步优化模型。并且通过将周期放大为100个月，可以发现，狐狸与兔子的数量变化在动态平衡状态运转，也符合基本常识。分析代码如下所示：

from scipy.integrate import solve_ivp
from scipy.optimize import fsolve
import numpy as np
def natural_convection(eta, y): # 将含有两个未知函数的高阶微分方程降阶，得到由2+3个一阶微分方程组成的方程组
  x1 = y[0] #x函数的0阶导，即x函数本身
  y1 = y[1]#y函数的0阶导，即y函数本身
  return 0.19074*x1-0.00483*x1*y1,-0.48289*y1+0.00954*x1*y1
  #返回的依次为1阶导，2高阶导。。。高阶导
t = np.linspace(0, 100,100)#变量取值
t_span = [0,500]#取值范围
init = np.array([60,30])#题目给的初值条件
curve = solve_ivp(natural_convection,t_span= t_span,y0= init, t_eval=t)
t = curve.t
data = curve.y
plt.rc('font',size =14)
plt.rc('font',family = 'SimHei')
plt.plot(t,data[0,:],'--',label = '兔拟合曲线')
plt.plot(t,data[1,:],'--',label = '狐拟合曲线')
t0 = np.array([0,1,2,3,4,5,6,8,10,12,14,16,18])
x0 = np.array([60,63,64,63,61,58,53,44,39,38,41,46,53])
y0= np.array([30,34,38,44,50,55,58,56,47,38,30,27,26])
plt.plot(t0,x0,label = '原观测兔子数量')
plt.plot(t0,y0,label = '原观测狐狸数量')
plt.legend(loc = 'best',fontsize = 7)
plt.show()

四、总结

        捕食者与被捕食者模型几乎是生态动力学分析的基础。了解这种模型对于微分方程的学习和基本动力学模型的学习都有帮助。但这种模型整体上还是过于简单，之后可能会增加更多的元素。