【目标检测】36、OTA: Optimal Transport Assignment for Object Detection

论文：Optimal Transport Assignment for Object Detection

代码：https://github.com/Megvii-BaseDetection/OTA

出处：CVPR2021

贡献：

• 提出了一种基于优化策略的标签分配方式，Optimal Transport Assignment (OTA)，将 gt 看做 label 供应商，anchor 看做 label 需求方。对于正样本，将分类和回归的 loss 加权和作为传输花费，对于负样本，传输花费就为分类 loss，通过最小化该花费，让网络自己学习最优的标签分配方式。
• 免去了手工选定参数的方式来实现标签分配，让网络自己选择每个 gt 对应的 anchor 数量，而非提前设定，也能够较好的解决模棱两可的 anchor 分配问题，提高网络对这部分 anchor 的处理效果
• 在 COCO 上实现了 40.7% AP

一、背景

Label assignment 在目标检测中非常重要，是一个预定义的规则，能够分配每个 anchor 的正负。RetinaNet 使用 IoU 来实现，FCOS 根据每个点是否在 gt box 内部来确定其正负。

这些方法忽略了一个问题：不同大小、形状、遮挡程度的目标，其 positive/negative 的判定条件应该是不同的。

所以就有一些方法使用动态的分配方法，来实现 label assignment。

• ATSS 根据统计信息，来分配正负样本
• Freeanchor、AutoAssign 等通过使用预测的 confidence score 来动态分配正负

作者认为，独立的给每个 gt 分配 pos/neg 不是最优的方法，缺失了上下文信息，当处理那些模棱两可的 anchor 时（如图 1 中的红色点，一个点处于多个 gt 中），上面的方法是靠手工的特征来选定属于哪个 gt 的（如 max-IoU、min-Area 等）。

CNN 的方法中，其实是 one-to-many 的形式，也就是一个 gt 会对应多个 anchor。

本文作者为了从 global 的层面来实现 CNN 中的 one-to-many assignment，将 label assignment 问题变成了一个 Optimal Transport（OT）问题（线性规划的一个特殊形式）。

如何从 global 层面来实现的呢？

作者考虑了整个 loss 的大小，而 loss 是由该图中的所有预测结果组成的，所以可以看做 global 层面。

二、方法

2.1 Optimal Transport

OT 是这样的一个问题：

• 假设有 m 个供货商（gt），n 个需求方（anchor）
• 第 $i$ 个供货商有 $s_i$ 单元的货物（一个 gt 对 $s_i$ 个 anchor 负责），第 $j$ 个需求方需要 $d_j$ 单元的货物（一个 anchor 只需要一个 label）
• 每个单元的货物从供货商 $i$ 到需求方 $j$ 的 Transporting cost 是 $cij$
• OT 问题的目标是寻找一个 transportation plan π*，让这个 Transporting cost 最小

2.2 OT for label assignment

把 OT 放到目标检测的问题中，假设有 m 个 gt，n 个 anchor（所有 FNP 层的 anchor 之和）

把 gt 看做 positive labels 的供货商，供应 label，能够对 k anchor 供应 positive label，也就是每个 gt 对 k 个 anchor 负责（$s_i=k,i=1,2,...,m$）

把 anchor 看做需求方，需要一个label（$d_j=1,j=1,2,...,n$）

把一个 positive label 从 $g{t}_i$ 传递到 anchor $a_j$ 的花费为 $c^{fg}$，则该花费就是 cls 和 reg loss 的加权和（分类可用 Focal loss，回归可用 IoU loss 等），这里是点对点的 loss 之和，也就是所有的 gt 和所有的 anchor 分别点对点求 loss：

• $\alpha$ 是平衡因子，被设置为 1.5

除过 positive assignment，还有很大一部分 anchor 是负样本，所以还引入了一个供应商——背景，来提供 negative labels。

标准的 OT 问题中，供货商和需求方的数量应该是一样的，所以，背景可以提供的 negative labels 的数量就是 $n-m\times k$，n 为 anchor 个数，m 为 gt 个数

将一个 negative label 从 background 传递到 anchor 的花费如下，只有分类的 loss：

• $\varphi$ 表示背景类

将 $c^{bg}\in R^{1\times n}$ 和 $c^{fg}\in R^{m\times n}$ concat 起来，就得到了最终的花费 $c\in R^{(m+1)\times n}$。其中 m 个 gt， n 个 anchor。

• 每个 gt 负责的 anchor 个数为 k
• 背景负责的 anchor 个数 = anchor 总数 n - 所有 gt 负责的 anchor 之和

每个供应商（gt 或 background）负责的 anchor 个数为 $s_i$，以 m 为区分，m+1 表示的就是 background：

有了花费、供应商、需求方后，最优传递方案 π* 可以使用 off-the-shelf Sinkhorn-Knopp Iteration 方法解该 OT 问题来得到。

具体图示见图 2 中的 cost matrix，每行为一个 gt，每个 gt 会分别计算其和每个 anchor 的花费，组成最终的 cost matrix。

得到了 π* 之后，可以通过把每个 anchor 分配到能给他供货最多（即提供 label 数量最多）的 gt 上去来实现最优 label assignment。

OT 的计算只需要矩阵乘法，可以使用 GPU 来加速，提高了约 20% 的训练时间，在测试时候是无多消耗的。

OTA 的结构如下：

OTA 的过程如下：

• 先经过推理，得到预测的 anchor 对应的类别和位置
• 确定每个 gt 负责的 anchor 个数 $s_i$（根据 Dynamic k 得到的）
• 确定 background 负责的 anchor 个数 $s_{m+1}$（n-s）
• 每个 anchor 需要的 label 都是 1 个
• 计算每个 gt 对所有 anchor 的 cost（包括分类 cost、回归 cost、center prior cost）
• 优化 cost，得到最优传输方案 π*
• 每个 gt 根据前面计算得到的负责的 anchor 个数，则选择该 gt 对应的该行中，前 top-k 个位置的 anchor 作为候选框
• 如果多个 gt 对应了一个 anchor，则在这几个 gt 中选择 cost 最小的，对该 anchor 负责

2.3 Center prior

1、Center prior

一般更关注 gt 中心区域采样的方法可以称为 center prior，OTA 是基于 global 的优化方法。理论上说 OTA 能够将任何处于 gt box 内部的 anchor 分配为正样本，但为了让模型更关注潜在的正样本区域（如 center area）来稳定训练过程，OTA 中也引入了 Center prior 的先验。

如何在 OTA 中引入 center prior 的先验：

• 引入的方法是在 cost matrix 中拼接了 center prior
• 对每个 gt，在每个 FPN level，选择距离 gt 中心 $r^2$ 内的 anchor 作为正样本
• 在 $r^2$ 之外的 anchor，会降低其被分配为正样本的可能性

2、不同大小的 r 的效果对比如下：

• 小的 r 表示只有很少的 anchor 会被分配为正，能够让网络更关注有用的信息
• 大的 r 表示会有更多的 anchor 会被分配为正，但会给网络带来一些不稳定因素
• 当 r 分别为 3/5/7 时，对应的 anchor 分别为 45/125/245（anchor 数量=$r^2$ * FPN levels）
• OTA 对 r 的大小是很敏感的。当 r=5 时，表现较好。

3、对模棱两可的 anchor 的处理方式对比

当多个目标重叠或距离很近的时候，就会出现一个 anchor 和多个 gt 相交的情况，之前的方法 Min area、Max IoU、Min loss 等方法都是使用手工选定的规则来处理的。

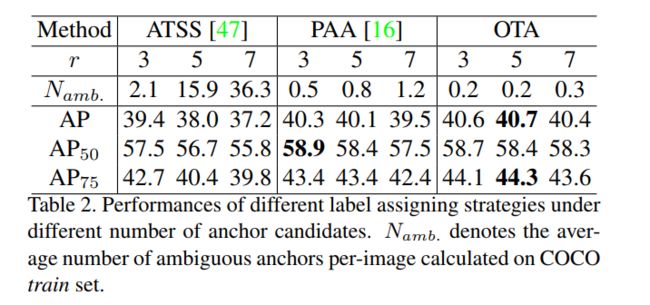
作者分别计算了 ATSS、PAA、OTA 中模棱两可 anchor 的数量，并且计算了不同 r 下对应的性能，见表 2。

• ATSS：随着 r 从 3 →7，模棱两可 anchor 的数量增长了很多，对应的 AP 从 39.4%→37.2%
• PAA：模棱两可 anchor 的数量和 r 不是很相关，但 AP 也下降了 0.8%，这应该是由于 PAA 使用了 Max IoU，对这些模棱两可的 anchor 不是很友好
• OTA：当多个 gt 都想要把自己的 label 传递给这个模棱两可的 anchor 的时候， OT 规则会根据 “最小全局花费” 的规则来解决这些冲突。所以 OTA 中的模棱两可的 anchor 数量少，且随着 r 没有很大的改变

图 3 中，红色箭头和虚线椭圆标明了模棱两可的位置，由于缺乏上下文和全局信息，ATSS 和 PAA 表现较差，OTA 在这里分配了很少的正样本，但有理由相信都是优质的样本。

2.4 Dynamic k Estimation

一般来说，每个 gt 对应的 anchor 数量应该是根据其尺寸、大小、遮挡比例等因素而改变的，所以难以直接根据这些因素建立一个映射关系来确定 gt 对应的 anchor 个数。

如何解决这种映射？——Dynamic k Estimation

作者提出了一个粗略的基于 IoU 的方法来估计每个 gt 对应的 positive anchor 数量。即选择 IoU 最大的前 q 个 anchor，将这 q 个 IoU 值相加，用做 anchor 的个数。

原理是什么呢？

作者认为，一个 gt 对应的合适的 anchor 个数和它周围的 well-regress 的 positive anchor 个数是正相关的，对比了动态的 k 和固定的 k 的效果如下：

不同大小 k 的效果对比如下：

当将 k 设置为固定数值时，随着 k 由小变大，AP 值是由小变大再变小的。

当 k=1 时，可以看做 one-to-one assigning strategy，但效果却不好，这说明是需要 one-to-many 的形式来实现好的效果的。

三、效果

1、实验设置

OTA 是一种 label assignment 的方法，是能够同时适用于 anchor-free 和 anchor-based 方法的，所以大多实验是基于 FCOS 的，还有一些基于 RetinaNet 等。

2、OTA 和其他方法结合的效果

OTA 超越了普通 FCOS 0.9%AP，和其他使用 IoU branch 等方法没差很大，使用 Dynamic k 提升到了 40.7%AP。
3、和 SOTA 的对比

四、OTA 代码片

    @torch.no_grad()
    def get_ground_truth(self, shifts, targets, box_cls, box_delta, box_iou):

        gt_classes = []
        gt_shifts_deltas = []
        gt_ious = []
        assigned_units = []

        box_cls = [permute_to_N_HWA_K(x, self.num_classes) for x in box_cls]
        box_delta = [permute_to_N_HWA_K(x, 4) for x in box_delta]
        box_iou = [permute_to_N_HWA_K(x, 1) for x in box_iou]

        box_cls = torch.cat(box_cls, dim=1)
        box_delta = torch.cat(box_delta, dim=1)
        box_iou = torch.cat(box_iou, dim=1)

        for shifts_per_image, targets_per_image, box_cls_per_image, \
                box_delta_per_image, box_iou_per_image in zip(
                    shifts, targets, box_cls, box_delta, box_iou):

            shifts_over_all = torch.cat(shifts_per_image, dim=0)

            gt_boxes = targets_per_image.gt_boxes

            # In gt box and center.
            deltas = self.shift2box_transform.get_deltas(
                shifts_over_all, gt_boxes.tensor.unsqueeze(1))
            is_in_boxes = deltas.min(dim=-1).values > 0.01

            center_sampling_radius = 2.5
            centers = gt_boxes.get_centers()
            is_in_centers = []
            for stride, shifts_i in zip(self.fpn_strides, shifts_per_image):
                radius = stride * center_sampling_radius
                center_boxes = torch.cat((
                    torch.max(centers - radius, gt_boxes.tensor[:, :2]),
                    torch.min(centers + radius, gt_boxes.tensor[:, 2:]),
                ), dim=-1)
                center_deltas = self.shift2box_transform.get_deltas(
                    shifts_i, center_boxes.unsqueeze(1))
                is_in_centers.append(center_deltas.min(dim=-1).values > 0)
            is_in_centers = torch.cat(is_in_centers, dim=1)
            del centers, center_boxes, deltas, center_deltas
            is_in_boxes = (is_in_boxes & is_in_centers)

            num_gt = len(targets_per_image)
            num_anchor = len(shifts_over_all)
            shape = (num_gt, num_anchor, -1)

            gt_cls_per_image = F.one_hot(
                targets_per_image.gt_classes, self.num_classes
            ).float()

            with torch.no_grad():
                loss_cls = sigmoid_focal_loss_jit(
                    box_cls_per_image.unsqueeze(0).expand(shape),
                    gt_cls_per_image.unsqueeze(1).expand(shape),
                    alpha=self.focal_loss_alpha,
                    gamma=self.focal_loss_gamma,
                ).sum(dim=-1)

                loss_cls_bg = sigmoid_focal_loss_jit(
                    box_cls_per_image,
                    torch.zeros_like(box_cls_per_image),
                    alpha=self.focal_loss_alpha,
                    gamma=self.focal_loss_gamma,
                ).sum(dim=-1)

                gt_delta_per_image = self.shift2box_transform.get_deltas(
                    shifts_over_all, gt_boxes.tensor.unsqueeze(1)
                )

                ious, loss_delta = get_ious_and_iou_loss(
                    box_delta_per_image.unsqueeze(0).expand(shape),
                    gt_delta_per_image,
                    box_mode="ltrb",
                    loss_type='iou'
                )

                loss = loss_cls + self.reg_weight * loss_delta + 1e6 * (1 - is_in_boxes.float())

                # Performing Dynamic k Estimation
                topk_ious, _ = torch.topk(ious * is_in_boxes.float(), self.top_candidates, dim=1)
                mu = ious.new_ones(num_gt + 1)
                mu[:-1] = torch.clamp(topk_ious.sum(1).int(), min=1).float()
                mu[-1] = num_anchor - mu[:-1].sum()
                nu = ious.new_ones(num_anchor)
                loss = torch.cat([loss, loss_cls_bg.unsqueeze(0)], dim=0)

                # Solving Optimal-Transportation-Plan pi via Sinkhorn-Iteration.
                _, pi = self.sinkhorn(mu, nu, loss)

                # Rescale pi so that the max pi for each gt equals to 1.
                rescale_factor, _ = pi.max(dim=1)
                pi = pi / rescale_factor.unsqueeze(1)

                max_assigned_units, matched_gt_inds = torch.max(pi, dim=0)
                gt_classes_i = targets_per_image.gt_classes.new_ones(num_anchor) * self.num_classes
                fg_mask = matched_gt_inds != num_gt
                gt_classes_i[fg_mask] = targets_per_image.gt_classes[matched_gt_inds[fg_mask]]
                gt_classes.append(gt_classes_i)
                assigned_units.append(max_assigned_units)

                box_target_per_image = gt_delta_per_image.new_zeros((num_anchor, 4))
                box_target_per_image[fg_mask] = \
                    gt_delta_per_image[matched_gt_inds[fg_mask], torch.arange(num_anchor)[fg_mask]]
                gt_shifts_deltas.append(box_target_per_image)

                gt_ious_per_image = ious.new_zeros((num_anchor, 1))
                gt_ious_per_image[fg_mask] = ious[matched_gt_inds[fg_mask],
                                                  torch.arange(num_anchor)[fg_mask]].unsqueeze(1)
                gt_ious.append(gt_ious_per_image)

        return torch.cat(gt_classes), torch.cat(gt_shifts_deltas), torch.cat(gt_ious)

五、SimOTA（源于 YOLOX）

SimOTA 是 YOLOX 中使用的 label assignment 的方式。都是旷世提出的方法。

在 OTA 中，总结了一个好的 label assignment 的方法一般有四个优点，且 OTA 也都满足了：

• Loss/quality aware
• Center prior
• Dynamic number of positive anchors for each $gt$
• Global view

OTA 将 label assignment 问题从 global 层面出发并看成了一个最优传输的问题，但 OTA 有一个问题，它需要使用 Sinkhorn-Knopp algorithm 来优化，这会增加 25% 的训练时间，假设使用 300 epoch，那增加的时长是不容小觑的。

所以孙剑等人又提出了 SimOTA，将 OTA 的优化过程简化为 dynamic top-k strategy，也就是不使用优化方法来优化 cost matirx，而是直接选择每个 gt 对应的花费最小的几个 anchor，使用该优化策略得到一个大概的解决方案。

SimOTA 是如何简化的？

• 求每个真值和 anchor 的传输花费 $c_{ij}$：在 SimOTA 中，真值 $g_i$ 和预测 anchor $p_j$ 的传输花费如下，$\lambda$ 是权重，其余两者分别为 $g_i$ 和 $p_j$ 的分类 loss 和回归 loss：
  
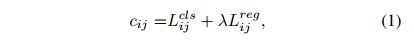
• 对于每个真值 $g_i$，在固定的 center 区域，选择花费最小的前 k 个 anchor，作为该 $g_i$ 所负责的 anchor。也就是不使用某种方法优化传输方式使得花费最小，而是直接选择计算后的 cost matrix 中，每行对应花费最小的 anchor。至于每个 gt 选择 k 个 anchor，这里的 $k$ 仍然使用 OTA 中的 Dynamic k Estimation 方法。

SimOTA 的优势：

• 降低了训练时间
• 避免了 Sinkhorn-Knopp algorithm 优化过程中的超参数
• 在 YOLOX 中，将 AP 从 45%→47.3%

SimOTA 代码片：

    def _assign(self,
                pred_scores,
                priors,
                decoded_bboxes,
                gt_bboxes,
                gt_labels,
                gt_bboxes_ignore=None,
                eps=1e-7):
        """Assign gt to priors using SimOTA.
        Args:
            pred_scores (Tensor): Classification scores of one image,
                a 2D-Tensor with shape [num_priors, num_classes]
            priors (Tensor): All priors of one image, a 2D-Tensor with shape
                [num_priors, 4] in [cx, xy, stride_w, stride_y] format.
            decoded_bboxes (Tensor): Predicted bboxes, a 2D-Tensor with shape
                [num_priors, 4] in [tl_x, tl_y, br_x, br_y] format.
            gt_bboxes (Tensor): Ground truth bboxes of one image, a 2D-Tensor
                with shape [num_gts, 4] in [tl_x, tl_y, br_x, br_y] format.
            gt_labels (Tensor): Ground truth labels of one image, a Tensor
                with shape [num_gts].
            gt_bboxes_ignore (Tensor, optional): Ground truth bboxes that are
                labelled as `ignored`, e.g., crowd boxes in COCO.
            eps (float): A value added to the denominator for numerical
                stability. Default 1e-7.
        Returns:
            :obj:`AssignResult`: The assigned result.
        """
        INF = 100000.0
        num_gt = gt_bboxes.size(0)
        num_bboxes = decoded_bboxes.size(0)

        # assign 0 by default
        assigned_gt_inds = decoded_bboxes.new_full((num_bboxes, ),
                                                   0,
                                                   dtype=torch.long)
        valid_mask, is_in_boxes_and_center = self.get_in_gt_and_in_center_info(
            priors, gt_bboxes)
        valid_decoded_bbox = decoded_bboxes[valid_mask]
        valid_pred_scores = pred_scores[valid_mask]
        num_valid = valid_decoded_bbox.size(0)

        if num_gt == 0 or num_bboxes == 0 or num_valid == 0:
            # No ground truth or boxes, return empty assignment
            max_overlaps = decoded_bboxes.new_zeros((num_bboxes, ))
            if num_gt == 0:
                # No truth, assign everything to background
                assigned_gt_inds[:] = 0
            if gt_labels is None:
                assigned_labels = None
            else:
                assigned_labels = decoded_bboxes.new_full((num_bboxes, ),
                                                          -1,
                                                          dtype=torch.long)
            return AssignResult(
                num_gt, assigned_gt_inds, max_overlaps, labels=assigned_labels)

        pairwise_ious = bbox_overlaps(valid_decoded_bbox, gt_bboxes)
        iou_cost = -torch.log(pairwise_ious + eps)

        gt_onehot_label = (
            F.one_hot(gt_labels.to(torch.int64),
                      pred_scores.shape[-1]).float().unsqueeze(0).repeat(
                          num_valid, 1, 1))

        valid_pred_scores = valid_pred_scores.unsqueeze(1).repeat(1, num_gt, 1)
        cls_cost = (
            F.binary_cross_entropy(
                valid_pred_scores.to(dtype=torch.float32).sqrt_(),
                gt_onehot_label,
                reduction='none',
            ).sum(-1).to(dtype=valid_pred_scores.dtype))

        cost_matrix = (
            cls_cost * self.cls_weight + iou_cost * self.iou_weight +
            (~is_in_boxes_and_center) * INF)

        matched_pred_ious, matched_gt_inds = \
            self.dynamic_k_matching(
                cost_matrix, pairwise_ious, num_gt, valid_mask)

        # convert to AssignResult format
        assigned_gt_inds[valid_mask] = matched_gt_inds + 1
        assigned_labels = assigned_gt_inds.new_full((num_bboxes, ), -1)
        assigned_labels[valid_mask] = gt_labels[matched_gt_inds].long()
        max_overlaps = assigned_gt_inds.new_full((num_bboxes, ),
                                                 -INF,
                                                 dtype=torch.float32)
        max_overlaps[valid_mask] = matched_pred_ious
        return AssignResult(
            num_gt, assigned_gt_inds, max_overlaps, labels=assigned_labels)

    def get_in_gt_and_in_center_info(self, priors, gt_bboxes):
        num_gt = gt_bboxes.size(0)

        repeated_x = priors[:, 0].unsqueeze(1).repeat(1, num_gt)
        repeated_y = priors[:, 1].unsqueeze(1).repeat(1, num_gt)
        repeated_stride_x = priors[:, 2].unsqueeze(1).repeat(1, num_gt)
        repeated_stride_y = priors[:, 3].unsqueeze(1).repeat(1, num_gt)

        # is prior centers in gt bboxes, shape: [n_prior, n_gt]
        l_ = repeated_x - gt_bboxes[:, 0]
        t_ = repeated_y - gt_bboxes[:, 1]
        r_ = gt_bboxes[:, 2] - repeated_x
        b_ = gt_bboxes[:, 3] - repeated_y

        deltas = torch.stack([l_, t_, r_, b_], dim=1)
        is_in_gts = deltas.min(dim=1).values > 0
        is_in_gts_all = is_in_gts.sum(dim=1) > 0

        # is prior centers in gt centers
        gt_cxs = (gt_bboxes[:, 0] + gt_bboxes[:, 2]) / 2.0
        gt_cys = (gt_bboxes[:, 1] + gt_bboxes[:, 3]) / 2.0
        ct_box_l = gt_cxs - self.center_radius * repeated_stride_x
        ct_box_t = gt_cys - self.center_radius * repeated_stride_y
        ct_box_r = gt_cxs + self.center_radius * repeated_stride_x
        ct_box_b = gt_cys + self.center_radius * repeated_stride_y

        cl_ = repeated_x - ct_box_l
        ct_ = repeated_y - ct_box_t
        cr_ = ct_box_r - repeated_x
        cb_ = ct_box_b - repeated_y

        ct_deltas = torch.stack([cl_, ct_, cr_, cb_], dim=1)
        is_in_cts = ct_deltas.min(dim=1).values > 0
        is_in_cts_all = is_in_cts.sum(dim=1) > 0

        # in boxes or in centers, shape: [num_priors]
        is_in_gts_or_centers = is_in_gts_all | is_in_cts_all

        # both in boxes and centers, shape: [num_fg, num_gt]
        is_in_boxes_and_centers = (
            is_in_gts[is_in_gts_or_centers, :]
            & is_in_cts[is_in_gts_or_centers, :])
        return is_in_gts_or_centers, is_in_boxes_and_centers

    def dynamic_k_matching(self, cost, pairwise_ious, num_gt, valid_mask):
        matching_matrix = torch.zeros_like(cost, dtype=torch.uint8)
        # select candidate topk ious for dynamic-k calculation
        candidate_topk = min(self.candidate_topk, pairwise_ious.size(0))
        topk_ious, _ = torch.topk(pairwise_ious, candidate_topk, dim=0)
        # calculate dynamic k for each gt
        dynamic_ks = torch.clamp(topk_ious.sum(0).int(), min=1)
        for gt_idx in range(num_gt):
            _, pos_idx = torch.topk(
                cost[:, gt_idx], k=dynamic_ks[gt_idx], largest=False)
            matching_matrix[:, gt_idx][pos_idx] = 1

        del topk_ious, dynamic_ks, pos_idx

        prior_match_gt_mask = matching_matrix.sum(1) > 1
        if prior_match_gt_mask.sum() > 0:
            cost_min, cost_argmin = torch.min(
                cost[prior_match_gt_mask, :], dim=1)
            matching_matrix[prior_match_gt_mask, :] *= 0
            matching_matrix[prior_match_gt_mask, cost_argmin] = 1
        # get foreground mask inside box and center prior
        fg_mask_inboxes = matching_matrix.sum(1) > 0
        valid_mask[valid_mask.clone()] = fg_mask_inboxes

        matched_gt_inds = matching_matrix[fg_mask_inboxes, :].argmax(1)
        matched_pred_ious = (matching_matrix *
                             pairwise_ious).sum(1)[fg_mask_inboxes]
        return matched_pred_ious, matched_gt_inds