tf.image.resize(双线性插值)功能复现(python)
文章目录
前言
一、Tensorflow中的resize功能简介
二、双线性插值原理简介
1.原理图
2.文字说明:
3.Python形式复现:
4.结果展示:
前言
复现一个功能可以让自己对这个功能的理解更加深入。(原创不易,欢迎转载)
一、Tensorflow中的resize功能简介
很多库都有自己的resize功能,用来对图片进行尺度上面的缩放,最常见的比如cv2.resize,tensorflow里面的tf.image.resize等等。从方法的角度来讲,最常见的resize插值方法有最邻近插值、双线性插值、双立方插值等。但就其效果来讲,双线性插值普遍用的多一些,其中tensorflow中的tf.image.resize便使用的是双线性插值的方法。下面使用Python以及matlab对其进行复现。
二、双线性插值原理简介
1.原理图
2.文字说明:
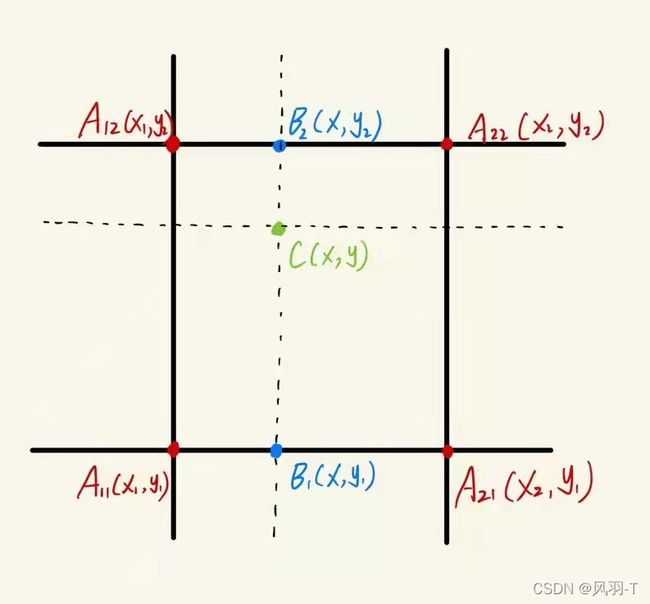
双线性插值,顾名思义,在两个方向分别进行一次线性插值。相当于在像素二维坐标系的X轴,Y轴上分别做两次临近的像素值权重分配。
如上图所示:
假设我们所要求的是C点的像素值,那么根据双线性插值方法,先对其做一个方向上的单线性插值,此处我们先对X轴方向(水平方向)做线性插值,即先求B1和B2两点的像素值。公式如下:
根据上述公式即可求出B1和B2两点的单线性插值,继而在Y轴(垂直方向)求最终C点的像素值。公式类似,如下:
如此便可求出C点的像素,运用了两次线性插值,故而得名双线性插值。
如需更深刻的理解可见参考文章:
(100条消息) 图像处理+双线性插值法_Tiramisu920的博客-CSDN博客_双线性插值法
3.Python形式复现:
直接上代码:
def bilinear(src, dst_h, dst_w):
src_h, src_w = src.shape[:2]
src_h_border = src_h - 1
src_w_border = src_w - 1
scale_x = src_w / dst_w
scale_y = src_h / dst_h
channel = src.shape[2]
dst = np.zeros([dst_h, dst_w, channel])
for c in range(channel):
for dst_y in range(dst_h):
for dst_x in range(dst_w):
# 目标在源上的坐标
src_x = (dst_x + 0.5) * scale_x - 0.5
src_y = (dst_y + 0.5) * scale_y - 0.5
# 计算在源图上四个近邻点的位置
src_x_0 = max(int(np.floor(src_x)), 0)
src_y_0 = max(int(np.floor(src_y)), 0)
src_x_1 = min(src_x_0 + 1, src_w - 1)
src_y_1 = min(src_y_0 + 1, src_h - 1)
# 处理黑边问题(插值后边界值为0或近0)
# 处理方式是复制边界值
# x_0和x_1一定不能相等,同理y_0和y_1一定不能相等,否则会出现黑边
if src_x_0 == src_x_1 and src_x_0 == src_w - 1:
src_x_0 = max(src_x_0 - 1, 0)
if src_y_0 == src_y_1 and src_y_0 == src_h - 1:
src_y_0 = max(src_y_0 - 1, 0)
if src_x < 0.0:
# 左上角顶点
if (src_x < 0.0) & (src_y < 0.0):
dst[dst_y, dst_x, c] = src[0, 0, c]
# 左下角顶点
elif (src_x < 0.0) & (src_y > src_h_border):
dst[dst_y, dst_x, c] = src[src_h_border, 0, c]
# 左超出边界
else:
dst[dst_y, dst_x, c] = (src_y_1 - src_y) * src[src_y_0, 0, c] + \
(src_y - src_y_0) * src[src_y_1, 0, c]
elif src_y < 0.0:
# 右上角顶点
if (src_x > src_w_border) & (src_y < 0.0):
dst[dst_y, dst_x, c] = src[0, src_w_border, c]
# 上超出边界
else:
dst[dst_y, dst_x, c] = (src_x_1 - src_x) * src[0, src_x_0, c] + \
(src_x - src_x_0) * src[0, src_x_1, c]
elif src_x > src_w_border:
# 右下角顶点
if(src_x > src_w_border) & (src_y > src_h_border):
dst[dst_y, dst_x, c] = src[src_h_border, src_w_border, c]
# 右超出边界
else:
dst[dst_y, dst_x, c] = (src_y_1 - src_y) * src[src_y_0, src_w_border, c] + \
(src_y - src_y_0) * src[src_y_1, src_w_border, c]
elif src_y > src_h_border:
# 下超出边界
dst[dst_y, dst_x, c] = (src_x_1 - src_x) * src[src_h_border, src_x_0, c] + \
(src_x - src_x_0) * src[src_h_border, src_x_1, c]
else:
# 双线性插值
value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, c] + \
(src_x - src_x_0) * src[src_y_0, src_x_1, c]
value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, c] + \
(src_x - src_x_0) * src[src_y_1, src_x_1, c]
dst[dst_y, dst_x, c] = (src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1
return dst代码部分说明:
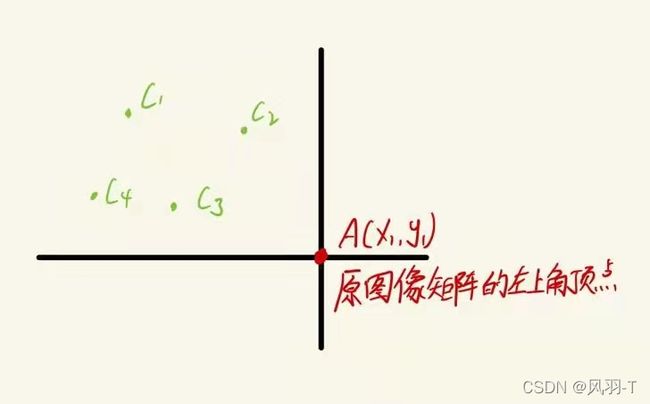
中间部分代码,即从注释# 左上角顶点,到# 下超出边界部分用了大量的if,else,原因在于放大图像时,其放大后的像素点有的会超出原像素矩阵。导致其不是规则的那种周围有四个相邻的,比如左上角这种只有1个像素点,如下图所示:
那么这些C点,其像素值就直接取左上角A点的值。
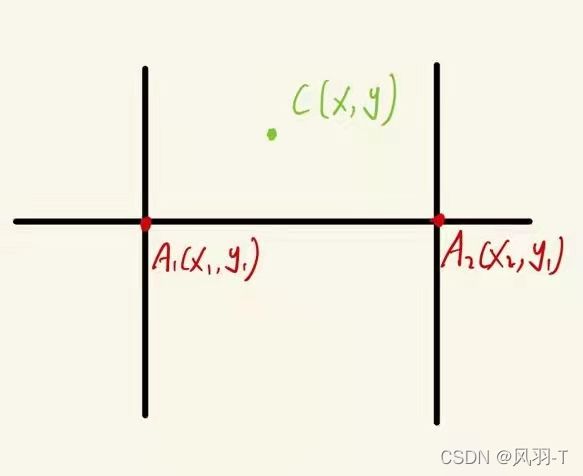
边界部分,如下图所示:
那么C点的取值只需要采用单线性插值即可,即C点的像素值等于A1和A2的像素值进行单线行插值。
(其他如果有小的细节,可参见代码部分)
4.结果展示:
通过结果对比,tf.image.resize和该复现代码得到的缩放图像误差均基本为0,此处就不放结果图,读者可自行实验。
5.Matlab复现部分跟这个基本原理一致,待后续更新。
2022.8.15更新matlab如下:
clear;
clc;
image = imread();
dst = resize_tf(image, 300, 200);
% save('dst');
% dst2 = dst / 256;
dst = uint8(dst);
% 显示原图像
figure;
imshow(image);
title("original Image");
% 显示新图像
figure;
imshow(dst);
title("New Image");
function [dst] = resize_tf(src, dst_h, dst_w)
[src_h, src_w, channel] = size(src);
% 此处为resize目标图像的尺寸
src_h_border = src_h;
src_w_border = src_w;
scale_x = src_w / dst_w;
scale_y = src_h / dst_h;
dst = zeros([dst_h, dst_w, channel]);
for c = 1:channel
for dst_y = 1:dst_h
for dst_x = 1:dst_w
y = uint16(dst_y);
x = uint16(dst_x);
% 计算目标在原图上的位置
src_x = (dst_x - 0.5) * scale_x + 0.5;
src_y = (dst_y - 0.5) * scale_y + 0.5;
%计算在原图上四个近邻点的位置
src_x_0 = max(floor(src_x), 1);
src_y_0 = max(floor(src_y), 1);
src_x_1 = min(src_x_0 + 1, src_w );
src_y_1 = min(src_y_0 + 1, src_h );
%处理黑边问题(插值后边界值为0或近0)
%处理方式是复制边界值
%x_0和x_1一定不能相等,同理y_0和y_1一定不能相等,否则会出现黑边
if src_x_0 == src_x_1 && src_x_0 == src_w
src_x_0 = max(src_x_0 - 1, 1);
end
if src_y_0 == src_y_1 && src_y_0 == src_h
src_y_0 = max(src_y_0 - 1 , 1);
end
%%%%%%%%%%%%
if src_x < 1
% 左上角顶点
if (src_x < 1) && (src_y < 1)
dst(dst_y, dst_x, c) = src(1, 1, c);
% 左下角顶点
elseif (src_x < 1) && (src_y > src_h_border)
dst(dst_y, dst_x, c) = src(src_h_border, 1, c);
% 左超出边界
else
dst(dst_y, dst_x, c) = (src_y_1 - src_y) * src(src_y_0, 1, c) + (src_y - src_y_0) * src(src_y_1, 1, c);
end
elseif src_y < 1
% 右上角顶点
if (src_x > src_w_border) && (src_y < 0)
dst(dst_y, dst_x, c) = src(1, src_w_border, c);
% 上超出边界
else
dst(dst_y, dst_x, c) = (src_x_1 - src_x) * src(1, src_x_0, c) + (src_x - src_x_0) * src(1, src_x_1, c);
end
elseif src_x > src_w_border
% 右下角顶点
if (src_x > src_w_border) && (src_y > src_h_border)
dst(dst_y, dst_x, c) = src(src_h_border, src_w_border, c);
% 右超出边界
else
dst(dst_y, dst_x, c) = (src_y_1 - src_y) * src(src_y_0, src_w_border, c) + (src_y - src_y_0) * src(src_y_1, src_w_border, c);
end
elseif src_y > src_h_border
% 下超出边界
dst(dst_y, dst_x, c) = (src_x_1 - src_x) * src(src_h_border, src_x_0, c) +(src_x - src_x_0) * src(src_h_border, src_x_1, c);
else
%双线性插值
img_left_up = double(src(src_y_0, src_x_0, c));
img_right_up = double(src(src_y_0, src_x_1, c));
img_left_down = double(src(src_y_1, src_x_0, c));
img_right_down = double(src(src_y_1, src_x_1, c));
value0 = (src_x_1 - src_x) * img_left_up +...
(src_x - src_x_0) * img_right_up;
value1 = (src_x_1 - src_x) * img_left_down +...
(src_x - src_x_0) *img_right_down;
result_temp = (src_y_1 - src_y) * value0 +...
(src_y - src_y_0) * value1;
dst(dst_y, dst_x, c) = result_temp;
end
end
end
end
end总结:
复现是很好的学习方法之一。