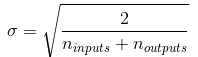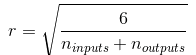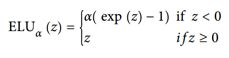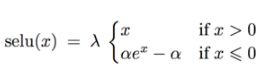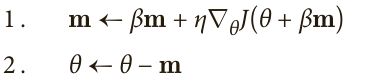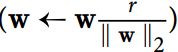机器学习实战11-训练深层神经网络
目录
一、梯度消失/爆炸问题
1.1、Xavier( Glorot)初始化(使用逻辑激活函数):
1.2、He 初始化(ReLU 激活函数及其变体,包括简称 ELU 激活):
1.3、非饱和激活函数
leaky ReLU
ELU
SELU
1.4、批量标准化
使用 TensorFlow 实现批量标准化
1.5、梯度裁剪
二、复用预训练层
2.1、复用 TensorFlow 模型
只有复用的模型文件时:
可以访问原始图形的Python代码
2.2、冻结较低层
2.3、Model Zoos
三、快速优化器
3.1、Momentum优化
3.2、Nesterov 加速梯度
3.3、AdaGrad算法
3.4、RMSProp
3.4、Adam 优化
3.5、训练稀疏模型
3.6、学习率调整
四、正则化避免过拟合
4.1、早期停止
4.2、L1 和 L2 正则化
创建一个正则方法函数
应用正则化方法到参数上
实例:
4.3、Dropout
4.4、最大范数正则化
如果你需要解决非常复杂的问题,例如检测高分辨率图像中的数百种类型的对象, 你可能需要训练更深的DNN,也许有 10 层,每层包含数百个神经元,通过数十万个连接来连接。:
- 首先,你将面临棘手的梯度消失问题(或相关的梯度爆炸问题),这会影响深度神经网络,并使较低层难以训练。
- 其次,对于如此庞大的网络,训练将非常缓慢。
- 第三,具有数百万参数的模型将会有严重的过拟合训练集的风险。
一、梯度消失/爆炸问题
反向传播算法的工作原理是从输出层到输入层,传播误差的梯度。 一旦该算法已经计算了网络中每个参数的损失函数的梯度,它就使用这些梯度来用梯度下降步骤来更新每个参数。
不幸的是,梯度往往变得越来越小,随着算法进展到较低层。 结果,梯度下降更新使得低层连接权重实际上保持不变,并且训练永远不会收敛到良好的解决方案。 这被称为梯度消失问题。 在某些情况下,可能会发生相反的情况:梯度可能变得越来越大,许多层得到了非常大的权重更新,算法发散。这是梯度爆炸的问题.
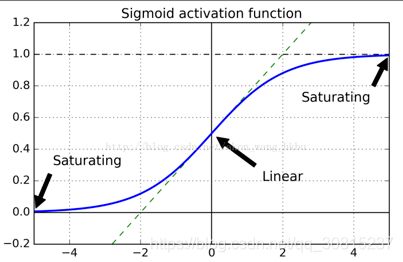
看一下逻辑激活函数,可以看到当输入变大(负或正)时,函数饱和在 0 或 1,导数非常接近 0。因此,当反向传播开始时, 它几乎没有梯度通过网络传播回来,而且由于反向传播通过顶层向下传递,所以存在的小梯度不断地被稀释,因此较低层确实没有任何东西可用。
1.1、Xavier( Glorot)初始化(针对逻辑激活函数):
针对这个问题提出了一个很有效的缓和办法。我们需要让信号在两个方向都正确流动。为了让信号正确流动,需要保持每一层的输入和输出的方差一致, 并且需要在反向流动过某一层时,前后的方差也要一致。
事实上,这是很难保证的,除非一层有相同数量的输入和输出连接, 一种很好的折中方案:连接权重必须按照下式进行随机初始化,其中 ![]() 和
和![]() 是权重被初始化层的输入和输出连接数(也称为扇入和扇出)。这种初始化的方法称为Xavier初始化(赛维尔),有时也称为Glorot初始化。
是权重被初始化层的输入和输出连接数(也称为扇入和扇出)。这种初始化的方法称为Xavier初始化(赛维尔),有时也称为Glorot初始化。
均值为零和方差为![]() 的正态分布:
的正态分布:
或者一个在-r和+r之间的均匀分布,其中:
当输入连接的数量大致等于输出连接的数量时,可以得到更简单的等式 :
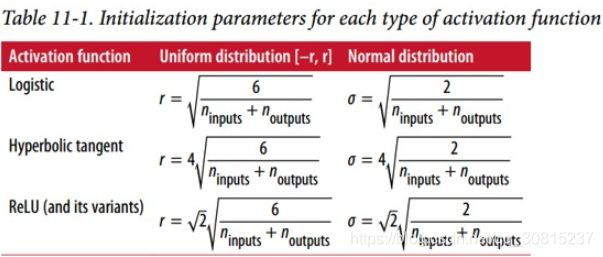
使用 Xavier 初始化策略可以大大加快训练速度。 最近的一些论文针对不同的激活函数提供了类似的策略,如下表所示
1.2、He 初始化(ReLU 激活函数及其变体,包括简称 ELU 激活):
He 初始化只考虑了扇入,而不是像 Xavier 初始化那样扇入和扇出之间的平均值。同样有正态分布和均匀分布两种初始方式: ![]()
默认情况下,fully_connected()函数使用 Xavier 初始化。 你可以通过variance_scaling_initializer() 函数来将其更改为 He 初始化:注意: 现在最好使用tf.layers.dense()。 dense()函数几乎与fully_connected()函数完全相同。
he_init = tf.variance_scaling_initializer()
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu,
kernel_initializer=he_init, name="hidden1") 这也是variance_scaling_initializer()函数的默认值,但可以通过设置参数mode ="FAN_AVG"来更改它。
正向传播时,状态值的方差保持不变;反向传播时,关于激活值的梯度的方差保持不变。
1.3、非饱和激活函数
消失/爆炸的梯度问题部分是由于激活函数的选择不好造成的。大多数人都认为,如果大自然在生物神经元中使用 sigmoid激活函数,它们必定是一个很好的选择。 但事实证明,其他激活函数在深度神经网络中表现得更好,特别是 ReLU线性整流激活函数,主要是因为它对正值不会饱和(也因为它的计算速度很快)。tf.nn.relu(features, name=None)
![]()
不幸的是, 它有一个被称为 “ReLU 死区” 的问题:在训练过程中,一些神经元有效地死亡,意味着它们停止输出 0 以外的任何东西。在某些情况下,你可能会发现你网络的一半神经元已经死亡,特别是如果你使用大学习率。 在训练期间,如果神经元的权重得到更新,使得神经元输入的加权和为负,则它将开始输出 0 。当这种情况发生时,由于当输入为负时,ReLU函数的梯度为0,神经元不可能恢复生机。
leaky ReLU
为了解决这个问题,你可能需要使用 ReLU 函数的一个变体,比如 leaky ReLU。这个函数定义为:
![]()
超参数alpha定义了函数“泄露”的程度:它是x < 0时函数的斜率,通常设置为 0.01。这个小斜坡确保 leaky ReLU 永不死亡;他们可能会长期昏迷,但他们有机会最终醒来。tf.nn.leaky_relu(features, alpha=0.2, name=None)
leaky Relu 总是优于严格的 ReLU 激活函数。事实上,设定α= 0.2(巨大 leak)似乎导致比α= 0.01(小 leak)更好的性能。他们还评估了随机化 leaky ReLU(RReLU),其中α在训练期间在给定范围内随机挑选,并在测试期间固定为平均值。它表现相当好,似乎是一个正则项。最后,他们还评估了参数 leaky ReLU(PReLU),其中α被授权在训练期间被学习(而不是超参数,它变成可以像任何其他参数一样被反向传播修改的参数)。 这在大型图像数据集上的表现强于 ReLU,但是对于较小的数据集,其具有过度拟合训练集的风险。
TensorFlow 没有针对 leaky ReLU 的预定义函数,但是很容易定义:
def leaky_relu(z, name=None):
return tf.maximum(0.01 * z, z, name=name)
hidden1 = tf.layers.dense(X, n_hidden1, activation=leaky_relu, name="hidden1")ELU
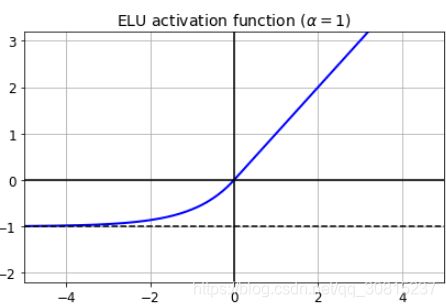
指数线性单元(exponential linear unit,ELU)的新的激活函数,在他们的实验中表现优于所有的 ReLU 变体:训练时间减少,神经网络在测试集上表现的更好。
它看起来很像 ReLU 函数,但有一些区别,主要区别在于:
- 首先它在
z < 0时取负值,这使得该单元的平均输出接近于 0。这有助于减轻梯度消失问题,如前所述。 超参数α定义为当z是一个大的负数时,ELU 函数接近的值。它通常设置为 1,但是如果你愿意,你可以像调整其他超参数一样调整它。 - 其次,它对
z < 0有一个非零的梯度,避免了神经元死亡的问题。 - 第三,函数在任何地方都是平滑的,包括
z = 0左右,这有助于加速梯度下降,因为它不会弹回z = 0的左侧和右侧。
ELU 激活函数的主要缺点:是计算速度慢于 ReLU 及其变体(由于使用指数函数),但是在训练过程中,这是通过更快的收敛速度来补偿的。 然而,在测试时间,ELU 网络将比 ReLU 网络慢。
TensorFlow 提供了一个可以用来建立神经网络的elu()函数,创建隐藏层时调用即可:
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.elu, name="hidden1")SELU
这个激活功能是由(https://arxiv.org/pdf/1706.02515.pdf)中提出的。 在训练期间,一个神经网络专门由使用SELU激活函数和LeCun初始化的一堆密集层将自我标准化:每层的输出将倾向于在训练期间保持相同的均值和方差, 这解决了消失/爆炸的梯度问题。因此,这种激活功能对于这样的神经网络来说非常显着地优于其他激活功能, 遗憾的是,SELU激活函数的自标准化特性很容易被破坏:你不能使用ℓ1或ℓ2 正则化, regular dropout, max-norm,跳过连接或其他非连续拓扑 (因此递归神经网络不会自我标准化)。但是,在实践中,它对顺序CNN非常有效。如果打破自我规范化,SELU不一定会胜过其他激活函数。
经过该激活函数后使得样本分布自动归一化到0均值和单位方差(自归一化,保证训练过程中梯度不会爆炸或消失,效果比Batch Normalization 要好) ,其实就是ELU乘了个lambda,关键在于这个lambda是大于1的。以前relu,prelu,elu这些激活函数,都是在负半轴坡度平缓,这样在activation的方差过大的时候可以让它减小,防止了梯度爆炸,但是正半轴坡度简单的设成了1。而selu的正半轴大于1,在方差过小的的时候可以让它增大,同时防止了梯度消失。这样激活函数就有一个不动点,网络深了以后每一层的输出都是均值为0方差为1。tensorflow中:
tf.nn.selu(features, name=None)使用哪个激活函数来处理深层神经网络的隐藏层?
一般 ELU > leaky ReLU(及其变体)> ReLU > tanh > sigmoid。 如果您关心运行时性能,那么您可能喜欢 leaky ReLU超过ELU。 如果你不想调整另一个超参数,你可以使用前面提到的默认的α值(leaky ReLU 为 0.01,ELU 为 1)。 特别是如果神经网络过拟合,则为RReLU; 如果拥有庞大的训练数据集,则为 PReLU。
下面使用leaky Relu激活函数创建神经网络:
###########创建文件夹用于tensorboard可视化
from datetime import datetime
now = datetime.utcnow().strftime("%Y%m%d%H%M%S")
root_logdir = "tf_logs"
logdir = "{}/run-{}/".format(root_logdir, now)
#################创建一个新的图
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
reset_graph()
n_inputs = 28 * 28 # MNIST 数据集每个实例的像素数
n_hidden1 = 300 #第一层神经元个数
n_hidden2 = 100 #第二层神经元个数
n_outputs = 10 #10个输出,对应0到9
##########定义激活函数
def leaky_relu(z, name=None):
return tf.maximum(0.01 * z, z, name=name)#注意这里的maximum函数是tensorflow库里的
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=leaky_relu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=leaky_relu, name="hidden2")
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy=tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,logits=logits)#根据logits计算交叉熵,返回每个实例(0到9)的交叉熵的一维张量
loss=tf.reduce_mean(xentropy,name="loss")
learning_rate=0.01
with tf.name_scope("train"):
optimizer=tf.train.GradientDescentOptimizer(learning_rate)
train_op=optimizer.minimize(loss)
with tf.name_scope("eval"):
correct=tf.nn.in_top_k(logits,y,1)#检查最高的logit值对应类别是否正确,返回一维张量,bool类型
accuracy=tf.reduce_mean(tf.cast(correct,tf.float32))# 转化为浮点型,求平均
init=tf.global_variables_initializer()
saver=tf.train.Saver()
loss_summary=tf.summary.scalar("Loss",loss)#创建一个节点来求loss
file_writer=tf.summary.FileWriter(logdir,tf.get_default_graph())
(X_train,y_train),(X_test,y_test)=tf.keras.datasets.mnist.load_data()
X_train=X_train.astype(np.float32).reshape(-1,28*28)/255.0
X_test=X_test.astype(np.float32).reshape(-1,28*28)/255.0
y_atrain=y_train.astype(np.int32)
y_test=y_test.astype(np.int32)
X_valid,X_train=X_train[:5000],X_train[5000:]
y_valid,y_train=y_train[:5000],y_train[5000:]
def shuffle_batch(X,y,batch_size):
rnd_idx=np.random.permutation(len(X))
n_batches=len(X)//batch_size#向下取整
for batch_idx in np.array_split(rnd_idx,n_batches):
X_batch,y_batch=X[batch_idx],y[batch_idx]
yield X_batch,y_batch
n_epochs=10
batch_size=50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch,y_batch in shuffle_batch(X_train,y_train,batch_size):
summary_str = loss_summary.eval(feed_dict={X: X_batch, y: y_batch})
file_writer.add_summary(summary_str, epoch)
#sess.run(train_op,feed_dict={X:X_batch,y:y_batch})
if epoch%3==0:
acc_batch=accuracy.eval(feed_dict={X:X_batch,y:y_batch})
acc_valid=accuracy.eval(feed_dict={X:X_batch,y:y_batch})
print(epoch, "Batch accuracy:", acc_batch, "Validation accuracy:", acc_valid)
save_path = saver.save(sess, "./my_model_final.ckpt")
参数说明:
1、tf.layers.dense()函数:
TensorFlow 有许多方便的功能来创建标准的神经网络层, 例如fully_connected()函数和tf.layers.dense()函数,创建一个完全连接的层,其中所有输入都连接到图层中的所有神经元。 它使用正确的初始化策略来负责创建权重和偏置变量。fully_connected()默认情况下使用 ReLU 激活函数(我们可以使用activate_fn参数来更改它)。
dense()函数与fully_connected()函数几乎相同,除了一些细微的差别:
几个参数被重命名:scope变为name,activation_fn变为activation(同样_fn后缀从其他参数(如normalizer_fn)中删除),weights_initializer成为kernel_initializer等。默认激活现在是无,而不是tf.nn.relu。
2、sparse_softmax_cross_entropy_with_logits
我们需要定义我们用来训练的损失函数。 正如我们在第 4 章中对 Softmax 回归所做的那样,我们将使用交叉熵。交叉熵将惩罚估计目标类的概率较低的模型。 我们使用sparse_softmax_cross_entropy_with_logits()计算交叉熵:它根据“logit”计算交叉熵(即通过 softmax 激活函数之前的网络输出),并且期望以整数形式的标签(在例子中,从 0 到 9)。 这将给我们一个包含每个实例的交叉熵的一维张量。 然后,我们可以使用 TensorFlow 的reduce_mean()函数来计算所有实例的平均交叉熵。
1.4、批量标准化
算法本质原理就是这样:在网络的每一层输入的时候,又插入了一个归一化层,也就是先做一个归一化处理,然后再进入网络的下一层。不过归一化层,可不像我们想象的那么简单,它是一个可学习、有参数的网络层。
批量标准化(Batch Normalization,BN)的技术来解决梯度消失/爆炸问题,该技术包括在每层的激活函数之前在模型中添加操作,简单地对输入进行中心化和归一化,然后每层使用两个新参数(一个用于尺度变换,另一个用于偏移)对结果进行尺度变换和偏移。 换句话说,这个操作可以让模型学习到每层输入值的最佳尺度,均值。
为了对输入进行归零和归一化,算法需要估计输入的均值和标准差。 它通过评估当前小批量输入的均值和标准差(因此命名为“批量标准化”)来实现。 我们引入了这个可学习重构参数γ、β,让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是:
![]()
上面的公式中m指的是小批量中的实例数量。。
![]() 是整个小批量B的经验均值
是整个小批量B的经验均值
![]() 是经验性的标准差,也是来评估整个小批量的。
是经验性的标准差,也是来评估整个小批量的。
![]() 是以为零中心和标准化的输入。
是以为零中心和标准化的输入。
![]() 是层的缩放参数。
是层的缩放参数。
![]() 是层的移动参数(偏移量)
是层的移动参数(偏移量)
![]() 是一个很小的数字,以避免被零除(通常为
是一个很小的数字,以避免被零除(通常为10^-3)。 这被称为平滑项。
yi:是BN操作的输出:它是输入的缩放和移位版本。
在实现的时候,会在训练阶段记录下训练数据中平均mean和variance,记为moving_mean和moving_variance,并在测试阶段使用训练时的moving_mean和moving_variance进行计算,这也就是参数training的作用。另外,在实现时一般使用一个decay系数来逐步更新moving_mean和moving_variance:
moving_mean = moving_mean * decay + new_batch_mean * (1 - decay)
from:https://blog.csdn.net/huitailangyz/article/details/85015611
更多参见:https://blog.csdn.net/qq_30815237/article/details/88933753
在测试时,没有小批量计算经验均值和标准差,只需使用整个训练集的均值和标准差。 这些在训练期间使用移动平均值进行计算。 总的来说,每个批次标准化的层次都学习了四个参数:γ(标度),β(偏移),μ(平均值)和σ(标准差)。
这项技术大大改善了他们试验的所有深度神经网络。梯度消失问题大大减少了,他们可以使用饱和激活函数,如 tanh 甚至 sigmoid 激活函数。网络对权重初始化也不那么敏感。他们能够使用更大的学习率,显著加快了学习过程。
然而,批量标准化的确会增加模型的复杂性(尽管它不需要对输入数据进行标准化,因为第一个隐藏层会照顾到这一点,只要它是批量标准化的)。 此外,还存在运行时间的损失:由于每层所需的额外计算,神经网络的预测速度较慢。 您可能会发现,训练起初相当缓慢,而渐变下降正在寻找每层的最佳尺度和偏移量,但一旦找到合理的好值,它就会加速。
使用 TensorFlow 实现批量标准化
TensorFlow 提供了一个batch_normalization()函数,它简单地对输入进行居中和标准化,但是必须自己计算平均值和标准差(基于训练期间的小批量数据或测试过程中的完整数据集) 作为这个函数的参数,并且还必须处理缩放和偏移量参数的创建(并将它们传递给此函数)。 这是可行的,但不是最方便的方法。 相反,你应该使用batch_norm()函数,它为你处理所有这些。 您可以直接调用它,或者告诉fully_connected()函数使用它,如下面的代码所示:
注意:tensorflow.contrib.layers.batch_norm()已经不存在。现在最好使用tf.layers.batch_normalization(),明确地创建一个不同的层。 batch_normalization的参数与batch_norm()有些不同,特别是:
decay更名为momentumis_training被重命名为trainingupdates_collections被删除:批量标准化所需的更新操作被添加到UPDATE_OPS集合中,需要在训练期间运行这些操作- 不需要指定
scale = True,因为这是默认值。
还要注意,为了在每个隐藏层激活函数之前运行批量标准化,我们在批量规范层之后手动应用 RELU 激活函数。注意:由于tf.layers.dense()函数与本书中使用的tf.contrib.layers.arg_scope()不兼容,我们现在使用 python 的functools.partial()函数。 它可以很容易地创建一个my_dense_layer()函数,只需调用tf.layers.dense(),并自动设置所需的参数(除非在调用my_dense_layer()时覆盖它们)。
batch_norm_momentum=0.9
X=tf.placeholder(tf.float32,shape=(None,n_inputs),name="X")
y=tf.placeholder(tf.int32,shape=(None),name="y")
training=tf.placeholder_with_default(False,shape=(),name="training")##给Batch norm加一个placeholder
with tf.name_scope("dnn"):
he_init=tf.variance_scaling_initializer()
my_batch_norm_layer=partial(tf.layers.batch_normalization,training=training,momentum=batch_norm_momentum)
my_dense_layer=partial(tf.layers.dense,kernel_initializer=he_init)
hidden1=my_dense_layer(X,n_hidden1,name="hidden1")
bn1=tf.nn.elu(my_batch_norm_layer(hidden1))#手动应用激活函数
hidden2=my_dense_layer(bn1,n_hidden2,name="hidden2")
bn2=tf.nn.elu(my_batch_norm_layer(hidden2))
logits_before_bn=my_dense_layer(bn2,n_outputs,name="outputs")
logits=my_batch_norm_layer(logits_before_bn)
with tf.name_scope("loss"):
xentropy=tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,logits=logits)
loss=tf.reduce_mean(xentropy,name="Loss")
with tf.name_scope("train"):
optimizer=tf.train.GradientDescentOptimizer(learning_rate)
training_op=optimizer.minimize(loss)
with tf.name_scope("eval"):
correct=tf.nn.in_top_k(logits,y,1)
accuracy=tf.reduce_mean(tf.cast(correct,tf.float32))
init=tf.global_variables_initializer()
saver=tf.train.Saver()
#注意:由于我们使用的是 tf.layers.batch_normalization() 而不是 tf.contrib.layers.batch_norm(),
# 所以我们需要明确运行批量规范化所需的额外更新操作(sess.run([ training_op,extra_update_ops], ...)。
n_epochs = 20
batch_size = 200
extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run([training_op, extra_update_ops],
feed_dict={training: True, X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Validation accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt")请注意,您还可以这样更新操作:
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
extra_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(extra_update_ops):
training_op = optimizer.minimize(loss)
#This way, you would just have to evaluate the training_op during training, TensorFlow would automatically run the update operations as well:
sess.run(training_op, feed_dict={training: True, X: X_batch, y: y_batch})函数说明:
1、partial()
函数在执行时,要带上所有必要的参数进行调用。但是,有时参数可以在函数被调用之前提前获知。这种情况下,一个函数有一个或多个参数预先就能用上,以便函数能用更少的参数进行调用。例如:
def add(a,b):
....: return a+b
plus = partial(add,100)
plus(9)
Out[13]: 109
其实就是函数调用的时候,有多个参数,但是其中的一个参数已经知道了,我们可以通过这个参数重新绑定一个新的函数,然后去调用这个新函数。在本例中:
bn1 = tf.layers.batch_normalization(hidden1, training=training, momentum=0.9)变成了:
my_batch_norm_layer = partial(tf.layers.batch_normalization,training=training, momentum=0.9)
bn1 = my_batch_norm_layer(hidden1)
2、tf.GraphKeys.UPDATE_OPS
tf.GraphKeys.UPDATE_OPS,这是一个tensorflow的计算图中内置的一个集合,其中会保存一些需要在训练操作之前完成的操作,并配合tf.control_dependencies函数使用。在batch_norm中,即为更新mean和variance的操作。
batch_normalization中更新mean和variance的操作,需要保证它们在training_op前完成。这两个操作是在tensorflow的内部实现中自动被加入tf.GraphKeys.UPDATE_OPS这个集合的。
3、tf.control_dependencies
该函数保证其辖域中的操作必须要在该函数所传递的参数中的操作完成后再进行,在本例中:
with tf.control_dependencies(extra_update_ops):
training_op = optimizer.minimize(loss)
代表先完成extra_update_ops操作(即tf.GraphKeys.UPDATE_OPS,即(更新mean和variance的操作)),然后再进行training_op操作。
举一个简单例子如下:
import tensorflow as tf
a_1 = tf.Variable(1)
b_1 = tf.Variable(2)
update_op = tf.assign(a_1, 10)
add = tf.add(a_1, b_1)
a_2 = tf.Variable(1)
b_2 = tf.Variable(2)
update_op = tf.assign(a_2, 10)
with tf.control_dependencies([update_op]):
add_with_dependencies = tf.add(a_2, b_2)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
ans_1, ans_2 = sess.run([add, add_with_dependencies])
print("Add: ", ans_1)
print("Add_with_dependency: ", ans_2)
输出:
Add: 3
Add_with_dependency: 12
可以看到两组加法进行的对比,正常的计算图在计算add时是不会经过update_op操作的,因此在加法时a的值为1,但是采用tf.control_dependencies函数,可以控制在进行add前先完成update_op的操作,因此在加法时a的值为10,因此最后两种加法的结果不同。
from:tensorflow中的batch_norm以及tf.control_dependencies和tf.GraphKeys.UPDATE_OPS的探究
1.5、梯度裁剪
减少梯度爆炸问题的一种常用技术是在反向传播过程中简单地剪切梯度,使它们不超过某个阈值(这对于递归神经网络是非常有用的)。 这就是所谓的梯度裁剪。一般来说,人们更喜欢批量标准化,但了解梯度裁剪以及如何实现它仍然是有用的。
在 TensorFlow 中,优化器的minimize()函数负责计算梯度并应用它们,所以您必须首先调用优化器的compute_gradients()方法,然后使用clip_by_value()函数创建一个裁剪梯度的操作,最后创建一个操作来使用优化器的apply_gradients()方法应用裁剪梯度:
learning_rate=0.01
threshold = 1.0
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
grads_and_vars = optimizer.compute_gradients(loss)
capped_gvs = [(tf.clip_by_value(grad, -threshold, threshold), var)
for grad, var in grads_and_vars]
training_op = optimizer.apply_gradients(capped_gvs) 它将计算梯度,将它们裁剪到 -1.0 和 1.0 之间,并应用它们。 threhold是可以调整的超参数。
函数说明:
1、compute_gradients(loss,var_list=None,gate_gradients=GATE_OP,aggregation_method=None,colocate_gradients_with_ops =False,grad_loss=None)
作用:对于在变量列表(var_list)中的变量计算对于损失函数的梯度,这个函数返回一个(梯度,变量)对的列表,其中梯度就是相对应变量的梯度了。这是minimize()函数的第一个部分。
2、apply_gradients(grads_and_vars,global_step=None,name=None)
作用:把梯度“应用”到变量上面去。其实就是按照梯度下降的方式加到上面去。这是minimize()函数的第二个步骤。 返回一个应用的操作。
参数: grads_and_vars: compute_gradients()函数返回的(gradient, variable)对的列表
3、clip_by_value
tf.clip_by_value(A, min, max):输入一个张量A,把A中的每一个元素的值都压缩在min和max之间。小于min的让它等于min,大于max的元素的值等于max。
A = np.array([[1,1,2,4], [3,4,8,5]])
tf.clip_by_value(A, 2, 5))
输出:
[[2 2 2 4]
[3 4 5 5]]二、复用预训练层
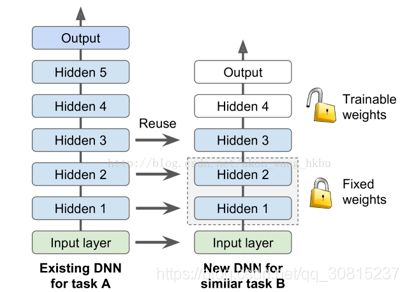
从零开始训练一个非常大的 DNN 通常不是一个好主意,相反,您应该总是尝试找到一个现有的神经网络来完成与您正在尝试解决的任务类似的任务,然后复用这个网络的较低层:这就是所谓的迁移学习。这不仅会大大加快训练速度,还将需要更少的训练数据。例如,假设您可以访问经过训练的 DNN,将图片分为 100 个不同的类别,包括动物,植物,车辆和日常物品。 您现在想要训练一个 DNN 来对特定类型的车辆进行分类。 这些任务非常相似,因此您应该尝试重新使用第一个网络的一部分。
2.1、复用 TensorFlow 模型
with tf.Session() as sess:
saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: mnist.test.images,
y: mnist.test.labels})
print(epoch, "Test accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_new_model_final.ckpt") 但是,一般情况下,您只需要重新使用原始模型的一部分(就像我们将要讨论的那样)。 一个简单的解决方案是将Saver配置为仅恢复原始模型中的一部分变量。
只有复用的模型文件时:
我们使用import_meta_graph(),它将加载整个图形,但您可以简单地忽略您不需要的部分。 在这个例子中,我们在预训练的第3层顶部添加了一个新的第4个隐藏层(忽略旧的第4个隐藏层)。 我们还构建了一个新的输出层,这个新输出的损失,以及一个新的优化器来最小化它。 我们还需要另一个保存程序来保存整个图形(包含整个旧图形和新操作),以及初始化操作以初始化所有新变量:
reset_graph()
saver = tf.train.import_meta_graph("./my_model_final.ckpt.meta")
#Next you need to get a handle on all the operations you will need for training.
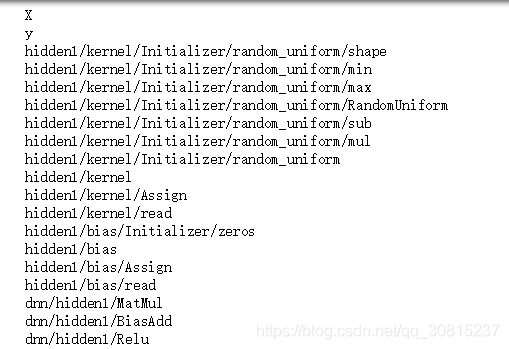
#If you don't know the graph's structure, you can list all the operations:
for op in tf.get_default_graph().get_operations():
print(op.name)添加了一个新的隐藏层。构建了一个新的输出层,新输出的损失,以及一个新的优化器/。
n_hidden4 = 20 # new layer
n_outputs = 10 # new layer
X = tf.get_default_graph().get_tensor_by_name("X:0")
y = tf.get_default_graph().get_tensor_by_name("y:0")
hidden3 = tf.get_default_graph().get_tensor_by_name("dnn/hidden3/Relu:0")
new_hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="new_hidden4")
new_logits = tf.layers.dense(new_hidden4, n_outputs, name="new_outputs")
with tf.name_scope("new_loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=new_logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("new_eval"):
correct = tf.nn.in_top_k(new_logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
with tf.name_scope("new_train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
new_saver = tf.train.Saver()
#执行
with tf.Session() as sess:
init.run()
saver.restore(sess, "./my_model_final.ckpt")#加载旧模型
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Validation accuracy:", accuracy_val)
save_path = new_saver.save(sess, "./my_new_model_final.ckpt")#保存新模型可以访问原始图形的Python代码
如果你可以访问构建原始图形的Python代码,则可以重用所需的部分并删除其余部分:(上面的情况是只有原模型文件)
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300 # reused
n_hidden2 = 50 # reused
n_hidden3 = 50 # reused
n_hidden4 = 20 # new!
n_outputs = 10 # new!
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1") # reused
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name="hidden2") # reused
hidden3 = tf.layers.dense(hidden2, n_hidden3, activation=tf.nn.relu, name="hidden3") # reused
hidden4 = tf.layers.dense(hidden3, n_hidden4, activation=tf.nn.relu, name="hidden4") # new!
logits = tf.layers.dense(hidden4, n_outputs, name="outputs") # new!
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
#创建一个restore_saver来恢复预训练模型(为其提供要恢复的变量列表,否则它会抱怨图形不匹配)
reuse_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES,
scope="hidden[123]") # regular expression
restore_saver = tf.train.Saver(reuse_vars) # to restore layers 1-3
init = tf.global_variables_initializer()
saver = tf.train.Saver()
with tf.Session() as sess:
init.run()
restore_saver.restore(sess, "./my_model_final.ckpt")
for epoch in range(n_epochs): # not shown in the book
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size): # not shown
sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) # not shown
accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid}) # not shown
print(epoch, "Validation accuracy:", accuracy_val) # not shown
save_path = saver.save(sess, "./my_new_model_final.ckpt")2.2、冻结较低层
第一个 DNN 的较低层可能已经学会了检测图片中的低级特征,这将在两个图像分类任务中有用,因此您可以按照原样重新使用这些层。 在训练新的 DNN 时,“冻结”权重通常是一个好主意:如果较低层权重是固定的,那么较高层权重将更容易训练(因为他们不需要学习一个移动的目标)。 要在训练期间冻结较低层,最简单的解决方案是给优化器列出要训练的变量,不包括来自较低层的变量:
第一行获得隐藏层 3 和 4 以及输出层中所有可训练变量的列表。 这留下了隐藏层 1 和 2 中的变量。接下来,我们将这个受限制的可列表变量列表提供给optimizer的minimize()函数。现在,层 1 和层 2 被冻结:在训练过程中不会发生变化(通常称为冻结层)。
with tf.name_scope("train"): # not shown in the book
optimizer = tf.train.GradientDescentOptimizer(learning_rate) # not shown
train_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES,#在训练期间冻结较低层,最简单的解决方案是给优化器列出要训练的变量,不包括来自较低层的变量:
scope="hidden[34]|outputs")
training_op = optimizer.minimize(loss, var_list=train_vars)2.3、Model Zoos
你在哪里可以找到一个类似于你想要解决的任务训练的神经网络? 首先看看显然是在你自己的模型目录。 这是保存所有模型并组织它们的一个很好的理由,以便您以后可以轻松地检索它们。 另一个选择是在模型动物园中搜索。 许多人为了各种不同的任务而训练机器学习模型,并且善意地向公众发布预训练模型。
TensorFlow 在 https://github.com/tensorflow/models 中有自己的模型动物园。 特别是,它包含了大多数最先进的图像分类网络,如 VGG,Inception 和 ResNet ,包括代码,预训练模型和 工具来下载流行的图像数据集。
另一个流行的模型动物园是 Caffe 模型动物园。 它还包含许多在各种数据集(例如,ImageNet,Places 数据库,CIFAR10 等)上训练的计算机视觉模型(例如,LeNet,AlexNet,ZFNet,GoogLeNet,VGGNet,开始)。 Saumitro Dasgupta 写了一个转换器,可以在 https://github.com/ethereon/caffetensorflow。
三、快速优化器
到目前为止,我们已经看到了四种加速训练的方法(并且达到更好的解决方案):
- 对连接权重应用良好的初始化策略,
- 使用良好的激活函数,
- 使用批量规范化
- 重用预训练网络的部分。
另一个巨大的速度提升来自使用比普通渐变下降优化器更快的优化器。 在本节中,我们将介绍最流行的:动量优化,Nesterov 加速梯度,AdaGrad,RMSProp,最后是 Adam 优化。本节的结论是,您几乎总是应该使用Adam_optimization, 只需要这么小的改动,训练通常会快几倍。 但是,Adam 优化确实有三个可以调整的超参数(加上学习率)。 默认值通常工作的不错。 Adam 优化结合了来自其他优化算法的几个想法,所以先看看这些算法是有用的。
3.1、Momentum优化
想象一下,一个保龄球在一个光滑的表面上平缓的斜坡上滚动:它会缓慢地开始,但是它会很快地达到最终的速度(如果有一些摩擦或空气阻力的话)。 这是 Boris Polyak 在 1964 年提出的动量优化背后的一个非常简单的想法。相比之下,普通的梯度下降只需要沿着斜坡进行小的有规律的下降步骤,所以需要更多的时间才能到达底部。
梯度下降:只是通过直接减去损失函数J(θ)相对于权重θ的梯度,乘以学习率η来更新权重θ。 方程是:
![]()
它不关心早期的梯度是什么。 如果局部梯度很小,则会非常缓慢。
Momentum优化关注以前的梯度是多少:每一个迭代,会给momentum矢量m加本地梯度(乘以学习速率η),同时权重减去
momentum矢量 。换句话说,梯度被当作加速度来使用,而不是速度。为了模拟某种摩擦机制并防止动量m增长过大,该算法引入了一个新的超参数β,简称为动量,其必须设置在0(高摩擦)和1(无摩擦)之间。一个标准动量值为0.9。
![]()
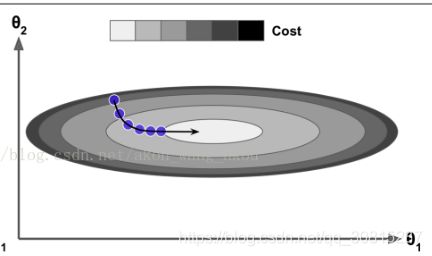
当梯度保持一个常量,最终速度(即权重变化的最大值)就等于梯度乘以学习速率η乘以1/(1-β)。如果β=0.9,那么最终速度等于10倍梯度乘以学习速率,所以Momentum优化最终会比梯度下降快10倍!这样就使得Momentum优化从平台逃离比梯度下降快得多。值得一提的是,在第4章中我们看到当输入的尺寸很特别时,成本函数看起来会像一个细长的碗。梯度下降在陡坡下降得非常快,但是在山谷中下降得很慢。相比较而言,Momentum优化会以越来越快的速度滑向谷底直到到达谷底(最佳)。在不使用批量归一化的深度神经网络中,高层最终常会产生不同尺寸的输入,因此使用Momentum优化会很有帮助,同时还会帮助跨过局部最优。
由于有动量,优化器可能会超调一点,然后返回,再超调,来回振荡多次后,最后稳定在最小值。这也是系统中要有一些摩擦的原因之一:它可以帮助摆脱振荡,从而加速收敛。
在TensorFlow中实现Momentum优化非常简单:只需用MomentumOptimizer替换GradientDescentOptimizer:
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
momentum=0.9)3.2、Nesterov 加速梯度
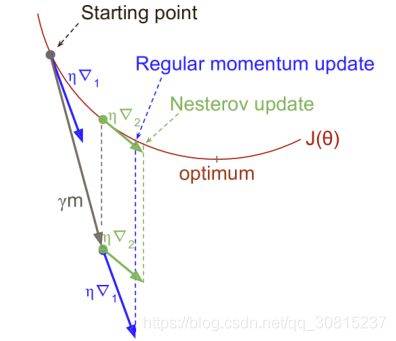
Yurii Nesterov 在 1983 年提出的动量优化的一个小变体几乎总是比普通的动量优化更快。 Nesterov 动量优化或 Nesterov 加速梯度(Nesterov Accelerated Gradient,NAG)的思想是测量损失函数的梯度不是在局部位置,而是在动量方向稍微靠前的位置。 与Vanilla Momentum优化唯一的不同就是用θ+βm来测量梯度,而不是θ。
回头看一下原始的Momentum:v = momentum * v - learning_rate * dx
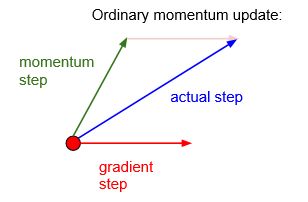
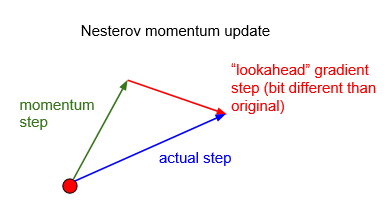
图中的momentum step(绿色的变量)代表代码中的动能项(momentum * v),gradient step (红色的变量)代表梯度也就是损失函数减少的方向( - learning_rate * dx),蓝色的线就是他们俩的向量和。
Nesterov Momentum要比Momentum的效果会好一些,我们先不管现输入是什么,所以在我们还没有计算出gradient step(红色的变量)情况下,我们已经建立了momentum step(绿色的变量),并得到了未知的梯度。也就是说,Nesterov Momentum想让我们来预测结果–gradient step,也就是计算在momentum step绿色箭头这一点的梯度确定gradient step,这样得到了和之前细微不同的更新结果,理论上,这一方法有着更好的收敛效果,在实际上确实要比Momentum好得多。
通俗的解释一下,由于从山顶往下滚的球会盲目地选择斜,Nesterov Momentum是在遇到倾斜向上之前应该减慢速度。
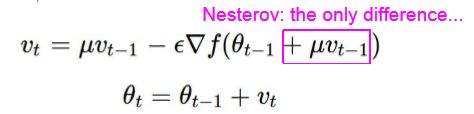
和之前Momentum不同的是,Nesterov Momentum在计算的梯度的时候,加上了μ*Vt-1,这种方式预估了下一次参数所在的位置,选择了和之前计算梯度不同的位置,称之为预测位置(lookahead position),所以Nesterov Momentum的效果会更好。
这个小调整有效是因为在通常情况下,动量矢量会指向正确的方向(即最优方向),所以在该方向相对远的地方使用梯度会比在原有地方更准确一些,正如下图所示(其中蓝线表示在起始点θ用成本函数测量的梯度,绿线表示在点θ+βm的梯度)。正如你所见,Nesterov更接近最优值。过一阵之后,这些小的改进叠加在一起,于是NAG就比常规Momentum优化明显增速很多。再者,注意到当动量把权重推过山谷时, 会跨过山谷并且推向更远,然而却往谷底的方向退回了一些。这有助于降低振荡,从而更快收敛。
对比Momentum优化,NAG几乎总能提高训练速度。要使用NGA,在创建Momentum Optimizer时只需简单地设置use_nesterov=True即可:
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate,
momentum=0.9, use_nesterov=True)3.3、AdaGrad算法
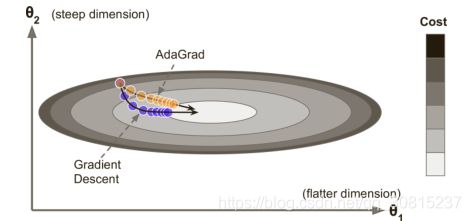
重新考虑一下细长碗的问题:梯度下降开始很快就走下最陡的斜坡,之后慢慢移动到谷底。如果算法可以早点检测到,并且修正方向往全局最优偏移一些就好了。AdaGrad 算法通过沿着最陡的维度缩小梯度向量来实现这一点:
![]()
第一步将梯度的平方累加到矢量s中(⊗符号表示矩阵乘法)。这个向量化形式相当于向量s的每个元素![]()
![]() 。换一种说法,每个
。换一种说法,每个 ![]()
![]()
i维陡峭,则在每次迭代时,![]()
第二步几乎与梯度下降相同,但有一个很大的不同:梯度矢量按比例缩小![]() (
(⊘符号表示矩阵除法,ε是避免被零除的平滑项,通常设置为 10^(-10)。 这个矢量化的形式相当于,对于所有参数 ![]() ,
,
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + le-7) 相比于SGD,增加了个附加变量—-cache来放缩梯度,并且是不停的增加这一附加变量。这里的变量cache是一个联合矢量,和主向量是一样大的,因为cache在每一维度计算其相应梯度的平方和,我们将这些cache构造起来,然后逐项用这一函数去除以cache的平方,使得对每个参数自适应不同的学习速率,对稀疏特征,得到大的学习更新,对非稀疏特征,得到较小的学习更新,因此该优化算法适合处理稀疏特征数据。举个栗子 :
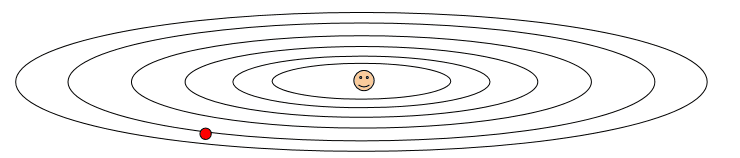
Adagrad在垂直方向上的梯度会加到cache中,然后相应的会除以越来越大的数,所以在垂直方向上会得到越来越小的更新。当我们在垂直方向上看到许多大的梯度,Adagrad就会衰减学习速率,使垂直方向的更新步长越来越小。在水平方向上的梯度是很小的,所以分母会变小,相比于垂直方向,水平方向更新更快。这就是对每个参数自适应不同的学习速率,针对不同梯度方向的补偿措施。
但是,此时,我们思考一个问题,如果我们训练整个神经网络,更新过程中步长大小会发生什么变化? 在Adagrad算法中,不断有正数加到分母的cache变量中,步长就会逐渐衰减到0,最后完全停止学习。
简而言之,这种算法会降低学习速度,但对于陡峭的尺寸,其速度要快于具有温和的斜率的尺寸。 这被称为自适应学习率。 它有助于将更新的结果更直接地指向全局最优,另一个附加的好处是只需对学习速率超参数η做很少的调整。
optimizer = tf.train.AdagradOptimizer(learning_rate=learning_rate)AdaGrad对于简单的二次问题一般表现都不错,但是在训练神经网络时却经常很早就停滞了。学习速率缩小得很多,在到达全局最优前算法就停止了。所以尽管TensorFlow有AdagradOptimizer,你也不要用它来训练深度神经网络。
3.4、RMSProp
尽管 AdaGrad 的速度变慢了一点,并且从未收敛到全局最优,但是 RMSProp算法通过仅累积最近迭代(而不是从训练开始以来的所有梯度)的梯度来修正这个问题。 它通过在第一步中使用指数衰减来实现:
![]()
RMSProp主要的思想是:cache不再是每一维度计算平方和,而是变成一个“泄露”的变量,利用衰减率(decay_rate)这个超参数,通常将decay_rate设置为0.9,接着计算引入衰减率发生“泄露”的平方和。所以我们仍然保持了在梯度较大或较小方向上,对于更新步长的补偿效果,但是不会再发生更新停止的情况。
衰减率β通常设置为0.9。没错,这又是一个新的超参数,但是这个默认值一般表现都比较好,所以你基本不需要做任何微调。
TensorFlow有RMSPropOptimizer类:
optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate,
momentum=0.9, decay=0.9, epsilon=1e-10) 除去非常简单的问题,这个优化器的表现几乎全都优于AdaGrad。同时表现也基本都优于Momentum优化和NAG。事实上,
在Adam优化出现之前,它是众多研究者所推荐的优化算法。
3.4、Adam 优化
Adam [ˈædəm],代表自适应矩估计,结合了动量优化和RMSProp的思想:类似Momentum优化,它会跟踪过去梯度的指数衰减平均值,同时也类似RMSProp,它会跟踪过去梯度平方的指数衰减平均值。
![]()
T表示迭代数(从1开始)。
如果只看步骤1、步骤2和步骤5,你会发现Adam同Momentum优化以及RMSProp非常类似。唯一的不同是步骤1计算的是指数衰减的平均值而不是指数衰减的总和,但是除了常数因子以外,它们都是相等的(衰减平均值是1-β1 倍的衰减总和)。步骤3和步骤4是一种技术的细节:因为m和s初始化都为0,它们会在训练开始时相对0有一点偏移量,所以这两个步骤在训练开始时有助于提高m和s。
动量衰减超参数β1 通常被初始化为0.9,缩放衰减超参数β2通常被初始化为0.999。与之前一样,平滑项通常会设置为一个很小的数字,比如10^(-8) 。这些是TensorFlow的AdamOptimizer类的默认值,你可以使用:
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)实际上,因为Adam是一个自适应学习速率算法(与AdaGrad以及RMSProp类似),它需要对学习速率超参数η进行微调。你可以一直使用默认值η=0.001,这样使得Adam比梯度下降更容易使用。
3.5、训练稀疏模型
所有刚刚提出的优化算法都会产生密集的模型, 大多数参数都是非零的。 如果你在运行时需要一个非常快速的模型,或者如果你需要它占用较少的内存,你可能更喜欢用一个稀疏模型来代替。
实现这一点的方法是像平常一样训练模型,然后摆脱微小的权重(将它们设置为 0)。另一个选择是在训练过程中应用强 l1 正则化,因为它会推动优化器尽可能多地消除权重。最后一个选择是应用双重平均,通常称为遵循正则化领导者(FTRL),一种由尤里·涅斯捷罗夫(Yurii Nesterov)提出的技术。 当与 l1 正则化一起使用时,这种技术通常导致非常稀疏的模型。 TensorFlow 在FTRLOptimizer类中实现称为 FTRL-Proximal 的 FTRL 变体。
3.6、学习率调整
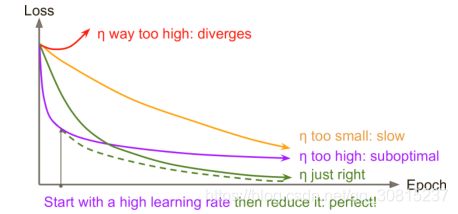
找到一个好的学习速度可能会非常棘手。如果设置得太低,训练最终会收敛到最佳状态,但这需要很长时间。 如果将其设置得太高,开始的进度会非常快,但最终会在最优解周围跳动,永远不会安顿下来(除非使用自适应学习率优化算法,如 AdaGrad,RMSProp 或 Adam,即使这样可能需要时间来解决)。 如果您的计算预算有限,那么您可能必须在正确收敛之前中断训练,产生次优解决方案。
相比一个固定的学习速率,你可以做得更好:如果你先以一个高学习速率开始,然后一旦它停止快速过程就降低速率,那么你会获得一个比最优固定学习速率更快速的方案。有很多不同的策略在训练过程中监督学习速率。这些策略称为学习计划,最常用有:
1、预定分段常数学习速率
开始设置学习速率η =0.1,在50个数据之后设置η =0.01。尽管这个方法效果不错,但是需要搞清楚正确的学习速率和何时使用。
2、性能调度
每N个步骤进行测量来验证错误(比如早期停止),然后当错误停止出现时,将学习速率降低到1/λ。
3、指数调度
将学习速率设置为迭代数t的函数:![]() 。这个效果很好,但是需要微调η 和r。学习速率每r步下降10。
。这个效果很好,但是需要微调η 和r。学习速率每r步下降10。
4、功率调度
设置学习速率为![]() 。超参数c通常设置为1。这个与指数调度类似,但是学习速率降低得非常慢。
。超参数c通常设置为1。这个与指数调度类似,但是学习速率降低得非常慢。
实验验证:性能调度和指数调度都表现良好,但更喜欢指数调度,因为它实现起来比较简单,容易调整,收敛速度略快于最佳解决方案。
使用 TensorFlow 实现学习率调整非常简单:
initial_learning_rate = 0.1
decay_steps = 10000
decay_rate = 1/10
global_step = tf.Variable(0, trainable=False, name="global_step")
learning_rate = tf.train.exponential_decay(initial_learning_rate, global_step,
decay_steps, decay_rate)
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
training_op = optimizer.minimize(loss, global_step=global_step)设置完超参数值后,我们创建一个不可训练变量global_step(初始化为0)来跟踪当前训练的迭代数。然后我们用TensorFlow的exponential_decay()函数定义一个指数衰减学习速率(其中η=0.1,r=10000)。接着,我们构建一个使用该衰减学习速率的优化器。最后,我们通过调用优化器的minimize()方法构建训练操作;因为我们给它传入了global_step变量,所以它会自增。
AdaGrad、RMSProp和Adam优化在训练中自动降低了学习速率,所以不需要额外加入学习计划。对于其他的优化算法,使用指数衰减或性能调度可以很有效地提高收敛速度。
四、正则化避免过拟合
深度神经网络通常具有数以万计的参数,有时甚至是数百万。 有了这么多的参数,网络拥有难以置信的自由度,可以适应各种复杂的数据集。 但是这个很大的灵活性也意味着它很容易过拟合训练集。 在本节中,我们将介绍一些最流行的神经网络正则化技术,以及如何用 TensorFlow 实现它们:早期停止法,l1 和 l2 正则化,drop out,最大范数正则化和数据增强。
4.1、早期停止
为避免过度拟合训练集,一个很好的解决方案就是尽早停止训练 :只要在验证集的性能开始下降时中断训练。
用TensorFlow实现提前停止的一种方法是定期对验证集进行模型评估(比如:每50步),同时如果表现好于前一个“优胜者”快照就将此“优胜者”快照保存起来。在保存最后一张“优胜者”快照的时候计算步数,当步数达到某些限制(比如:2000步)时停止训练。然后恢复最后一张“优胜者”快照。
尽管在练习中提前停止表现得很好,但通常你还是可以通过结合其他正则化技术来获得更高的性能。
4.2、L1 和 L2 正则化
就像对简单线性模型所做的那样, 可以使用 l1 和 l2 正则化约束一个神经网络的连接权重(但通常不是它的偏置)。使用 TensorFlow 做到这一点的一种方法是简单地将适当的正则化项添加到您的损失函数中。
tensorflow中对参数使用正则项分为两步:
- 创建一个正则方法(函数/对象)
- 将这个正则方法(函数/对象),应用到参数上
创建一个正则方法函数
tf.contrib.layers.l1_regularizer(scale, scope=None)返回一个用来执行L1正则化的函数,函数的签名是func(weights).
参数:scale: 正则项的系数.;scope: 可选的scope name
tf.contrib.layers.l2_regularizer(scale, scope=None)返回一个执行L2正则化的函数.
tf.contrib.layers.sum_regularizer(regularizer_list, scope=None)返回一个可以执行多种(个)正则化的函数.意思是,创建一个正则化方法,这个方法是多个正则化方法的混合体.
参数: regularizer_list: regulizer的列表
应用正则化方法到参数上
tf.contrib.layers.apply_regularization(regularizer, weights_list=None)参数:regularizer:上一步创建的正则化方法
weights_list: 想要执行正则化方法的参数列表,如果为None的话,就取GraphKeys.WEIGHTS中的weights.
函数返回一个标量Tensor,同时,这个标量Tensor也会保存到GraphKeys.REGULARIZATION_LOSSES中.这个Tensor保存了计算正则项损失的方法.
接下来,我们只需将这个正则项损失加到我们的损失函数上就可以了.
实例:
例如,假设您只有一个权重为weights1的隐藏层和一个权重为weight2的输出层,那么您可以像这样应用 l1 正则化:
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu, name="hidden1")
logits = tf.layers.dense(hidden1, n_outputs, name="outputs")
#将正则项添加到损失函数中
W1 = tf.get_default_graph().get_tensor_by_name("hidden1/kernel:0")#Returns the `Tensor` with the given `name`.
W2 = tf.get_default_graph().get_tensor_by_name("outputs/kernel:0")
scale = 0.001 # l1 regularization hyperparameter
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
logits=logits)
base_loss = tf.reduce_mean(xentropy, name="avg_xentropy")
reg_losses = tf.reduce_sum(tf.abs(W1)) + tf.reduce_sum(tf.abs(W2))
loss = tf.add(base_loss, scale * reg_losses, name="loss")
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 10
batch_size = 200
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Validation accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt") 我们可以将正则化函数传递给tf.layers.dense()函数,该函数将使用它来创建计算正则化损失的操作,并将这些操作添加到正则化损失集合中。设置内核正则化参数有l1_regularizer(),l2_regularizer(),l1_l2_regularizer()
reset_graph()
n_inputs = 28 * 28 # MNIST
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
scale=0.001
my_dense_layer = partial(tf.layers.dense, activation=tf.nn.relu,
kernel_regularizer=tf.contrib.layers.l1_regularizer(scale)) #添加l1正则函数
with tf.name_scope("dnn"):
hidden1 = my_dense_layer(X, n_hidden1, name="hidden1")
hidden2 = my_dense_layer(hidden1, n_hidden2, name="hidden2")
logits = my_dense_layer(hidden2, n_outputs, activation=None,name="outputs")
#将正则loss添加到loss
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
base_loss = tf.reduce_mean(xentropy, name="avg_xentropy")
reg_losses = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
loss = tf.add_n([base_loss] + reg_losses, name="loss")#实现一个列表的元素的相加。
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 10
batch_size = 200
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
accuracy_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
print(epoch, "Validation accuracy:", accuracy_val)
save_path = saver.save(sess, "./my_model_final.ckpt")不要忘记把正则化的损失加在你的整体损失上,否则就会被忽略。
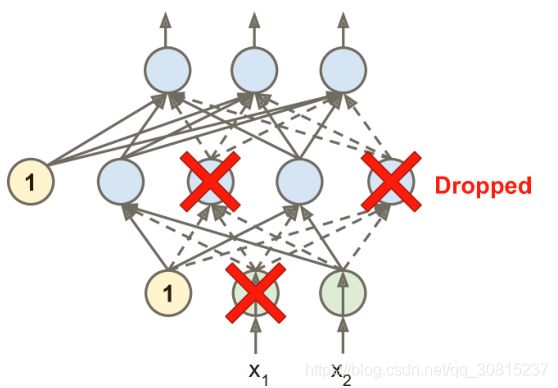
4.3、Dropout
深度神经网络最流行的正则化技术可以说是 dropout。并且已被证明是非常成功的:即使是最先进的神经网络,仅仅通过增加Dropout,就可以提高1-2%的准确度。 这听起来可能不是很多,但是当一个模型已经具有 95% 的准确率时,获得 2% 的准确度提升意味着将误差率降低近 40%(从 5% 误差降至大约 3%)。
这是一个相当简单的算法:在每个训练步骤中,每个神经元(包括输入神经元,但不包括输出神经元)都有一个暂时“丢弃”的概率p,这意味着在这个训练步骤中它将被完全忽略, 在下一步可能会激活 。 超参数p称为丢失率,通常设为 50%。 训练后神经元不会再下降。
这里提到一个很小但是很重要的技术细节。假设p=50,在测试期间,一个神经元将会被连接到训练期间输入神经元(平均)的两倍。为了弥补这个情况,我们需要在训练之后给每一个神经元的输入连接权重乘以0.5。更通俗来讲,我们需要在训练结束后给每一个输入连接权重乘以保持可能性(1-p)。
要用TensorFlow实现dropout,你可以直接在输入层和每一个隐藏层的输出调用dropout函数。在训练中,这个函数会随机丢弃一些项(把它们设置为0),并且给剩下的项除以保持可能性。tf.contrib.layers.dropout()已经不存在。 现在使用tf.layers.dropout()函数,有一些细微差别:
- 您必须指定丢失率(rate)而不是保持率(
keep_prob),其中rate简单地等于1 - keep_prob is_training参数被重命名为training。
training = tf.placeholder_with_default(False, shape=(), name='training')#训练时True,测试时False
dropout_rate = 0.5 # == 1 - keep_prob
X_drop = tf.layers.dropout(X, dropout_rate, training=training)
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X_drop, n_hidden1, activation=tf.nn.relu,
name="hidden1")
hidden1_drop = tf.layers.dropout(hidden1, dropout_rate, training=training)
hidden2 = tf.layers.dense(hidden1_drop, n_hidden2, activation=tf.nn.relu,
name="hidden2")
hidden2_drop = tf.layers.dropout(hidden2, dropout_rate, training=training)
logits = tf.layers.dense(hidden2_drop, n_outputs, name="outputs")如果观察到模型过拟合,则可以增加 dropout 率。 相反,如果模型欠拟合训练集,则应尝试降低 dropout 率。dropout 似乎减缓了收敛速度,但通常会在调整得当时使模型更好。 所以,这通常值得花费额外的时间和精力。
4.4、最大范数正则化
另一种在神经网络中非常流行的正则化技术被称为最大范数正则化:
对于每个神经元,它约束输入连接的权重w,使得 ![]() ,其中
,其中r是最大范数超参数,![]() 是 l2 范数。我们通常通过在每个训练步骤之后直接计算
是 l2 范数。我们通常通过在每个训练步骤之后直接计算 ![]() ,如果需要的话可以剪切:
,如果需要的话可以剪切:
减少r增加了正则化的数量,并有助于减少过拟合。 最大范数正则化还可以帮助减轻梯度消失/爆炸问题。
让我们回到 MNIST 的简单而简单的神经网络,只有两个隐藏层:
threshold = 1.0
weights = tf.get_default_graph().get_tensor_by_name("hidden1/kernel:0")
clipped_weights = tf.clip_by_norm(weights, clip_norm=threshold, axes=1)
clip_weights = tf.assign(weights, clipped_weights)
weights2 = tf.get_default_graph().get_tensor_by_name("hidden2/kernel:0")
clipped_weights2 = tf.clip_by_norm(weights2, clip_norm=threshold, axes=1)
clip_weights2 = tf.assign(weights2, clipped_weights2)1、tf.clip_by_norm(t,clip_norm):
参数:t 为要clip的tensor ; clip_norm:是一个阈值,计算规则是:
if clip_norm >= l2_norm
t = t
else
t = t*clip_norm/l2norm(t)
axes = 1对每一个行做l2_norm的clip_norm
axes = 0 就是对列做。
2、tf.assign(A, new_number): 这个函数的功能主要是把A的值变为new_number
另一种实现方法:定义一个max_norm_regularizer()函数:
def max_norm_regularizer(threshold, axes=1, name="max_norm",
collection="max_norm"):
def max_norm(weights):
clipped = tf.clip_by_norm(weights, clip_norm=threshold, axes=axes)
clip_weights = tf.assign(weights, clipped, name=name)
tf.add_to_collection(collection, clip_weights)
return None # there is no regularization loss term
return max_norm 可以调用这个函数来得到一个最大范数调节器(与你想要的阈值)。就是调用这个函数会返回一个函数。 当你创建一个隐藏层时,你可以将这个正则化器传递给kernel_regularizer参数
reset_graph()
n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 50
n_outputs = 10
learning_rate = 0.01
momentum = 0.9
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
max_norm_reg = max_norm_regularizer(threshold=1.0) # 得到一个最大范数调节器
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, activation=tf.nn.relu,
kernel_regularizer=max_norm_reg, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu,
kernel_regularizer=max_norm_reg, name="hidden2")
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
with tf.name_scope("train"):
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs=10
batch_size=50
clip_all_weights = tf.get_collection("max_norm") #把裁剪的权重取出来,从一个集合中取出全部变量,是一个列表
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
sess.run(clip_all_weights)
acc_valid = accuracy.eval(feed_dict={X: X_valid, y: y_valid}) # not shown
print(epoch, "Validation accuracy:", acc_valid) # not shown
save_path = saver.save(sess, "./my_model_final.ckpt") # not shown函数说明:
1.tf.add_to_collection(name,value)
功能:将变量添加到名为name的集合中去。
参数:(1)name:集合名(2)value:被添加的变量
2.tf.get_collection(key,scope=None)
功能:获取集合中的变量。
参数:(1)key:集合名
3.tf.add_n(inputs,name=None)
功能:以元素方式添加所有输入张量。
参数:(1)inputs:张量对象列表,每个对象具有相同的形状和类型。(2)name:操作的名称(可选)。
请注意,最大范数正则化不需要在整体损失函数中添加正则化损失项,所以max_norm()函数返回None。 但是,在每个训练步骤之后,仍需要运行clip_weights操作,因此您需要能够掌握它。 这就是为什么max_norm()函数将clip_weights节点添加到最大范数剪裁操作的集合中的原因。您需要获取这些裁剪操作并在每个训练步骤后运行它们。
4.5、数据增强
比如将原始图像翻转平移拉伸,从而是模型的训练数据集增大。数据增强已经是深度学习的必需步骤了,其对于模型的泛化能力增加普遍有效,但是不必做的太过,将原始数据量通过数据增加增加到2倍可以,但增加十倍百倍就只是增加了训练所需的时间,不会继续增加模型的泛化能力了。
官方文档:训练深层神经网络