matlab神经网络预测建模,浅层神经网络时序预测和建模

浅层神经网络时序预测和建模

动态神经网络擅长时序预测。要查看在开环形式、闭环形式和开环/闭环多步预测中应用 NARX 网络的示例，请参阅Multistep Neural Network Prediction。

提示

有关时序数据的深度学习，请参阅使用深度学习进行序列分类。

例如，假设您有 pH 中和过程的数据。您想要设计一个网络，该网络可以根据过去的 pH 值和过去的酸值以及流入水槽的液体的基本流速来预测水槽内溶液的 pH 值。总共有 2001 个时间步，您有它们的序列。

您可以用两种方法解决此问题：

通常最好从 GUI 开始，然后使用 GUI 自动生成命令行脚本。使用上述任一方法之前，第一步都是通过选择数据集来定义问题。每个 GUI 都可以访问许多样本数据集，您可以使用这些数据集来试验工具箱。如果您有要解决的特定问题，可以将您自己的数据加载到工作区中。下一节介绍数据格式。定义问题

要为工具箱定义时序问题，请将一组 TS 输入向量排列为一个元胞数组中的列。然后，将另一组 TS 目标向量(每个输入向量的正确输出向量)排列到另一个元胞数组中(有关静态和时序数据的数据格式的详细说明，请参阅数据结构)。但是，在有些情况下只需要有一个目标数据集。例如，您可以定义以下时序问题，在其中使用先前的序列值预测下一个值：

targets = {1 2 3 4 5};

下一节说明如何使用 Neural Network Time Series (ntstool) 来训练用于拟合时序数据集的网络。此示例使用工具箱附带的 pH 中和数据集。使用 Neural Network Time Series

如果需要，使用以下命令打开 Neural Network Start GUI：

nnstart

点击 Time Series App 打开 Neural Network Time Series。(您也可以使用命令 ntstool。)

请注意，该开始窗格不同于其他 GUI 的开始窗格。这是因为 ntstool 可用于解决三种不同类型的时序问题。

在第一类时序问题中，您要根据时序 y(t) 的过去值和另一个时序 x(t) 的过去值来预测前者的将来值。这种预测形式称为外因(外部)输入非线性自回归或 NARX(请参阅 NARX 网络(narxnet，closeloop))，可以写作如下形式：

y(t) = f(y(t – 1), ..., y(t – d), x(t – 1), ..., (t – d))

此模型可用于根据失业率、GDP 等经济变量预测股票或债券的将来值。它还可用于系统识别，其中模型表示动态系统，例如化工工艺、制造系统、机器人、航空航天器等。

在第二类时序问题中，只涉及一个序列。时序 y(t) 的将来值仅根据该时序的过去值进行预测。这种预测形式称为非线性自回归(或 NAR)，可以写作如下形式：

y(t) = f(y(t – 1), ..., y(t – d))

此模型也可用于预测金融工具，但不使用伴随序列。

第三类时序问题类似于第一类，它也涉及两个序列：一个输入序列 x(t) 和一个输出/目标序列 y(t)。这里您想要根据 x(t) 的先前值预测 y(t) 的值，但不知道 y(t) 的先前值。该输入/输出模型可以写作如下形式：

y(t) = f(x(t – 1), ..., x(t – d))

NARX 模型将提供比该输入-输出模型更好的预测，因为它使用包含在 y(t) 的先前值中的附加信息。但是，在某些应用中，y(t) 的先前值不可用。只有在这种情况下，才会使用输入-输出模型，而不是 NARX 模型。

对于此示例，选择 NARX 模型，然后点击 Next 继续。

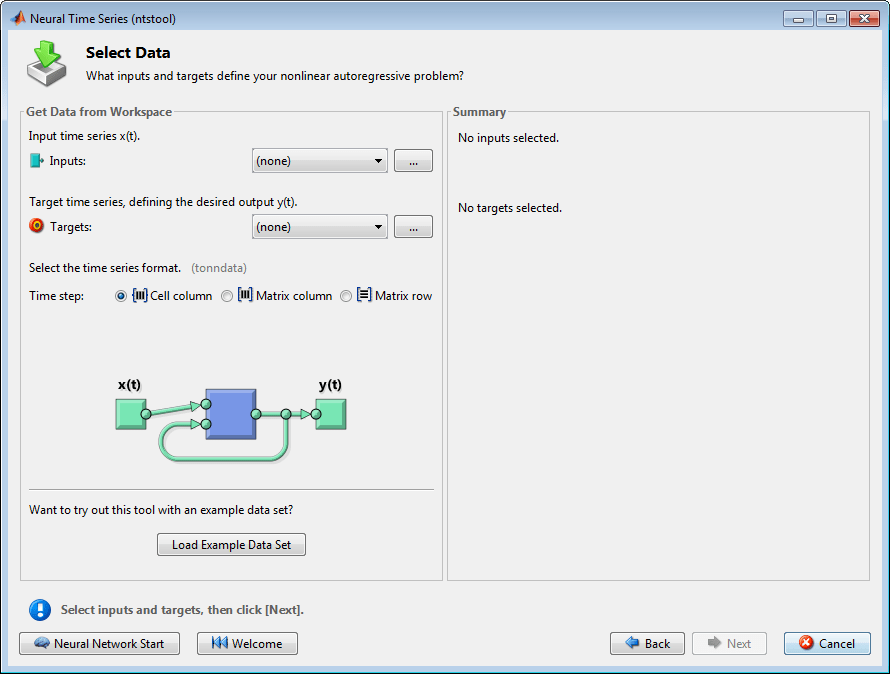
在 Select Data 窗口中点击 Load Example Data Set。将打开 Time Series Data Set Chooser 窗口。

注意

当您需要从 MATLAB® 工作区加载数据时，请使用 Select Data 窗口中的 Inputs 和 Targets 选项。

选择 pH Neutralization Process，然后点击 Import。这将返回 Select Data 窗口。

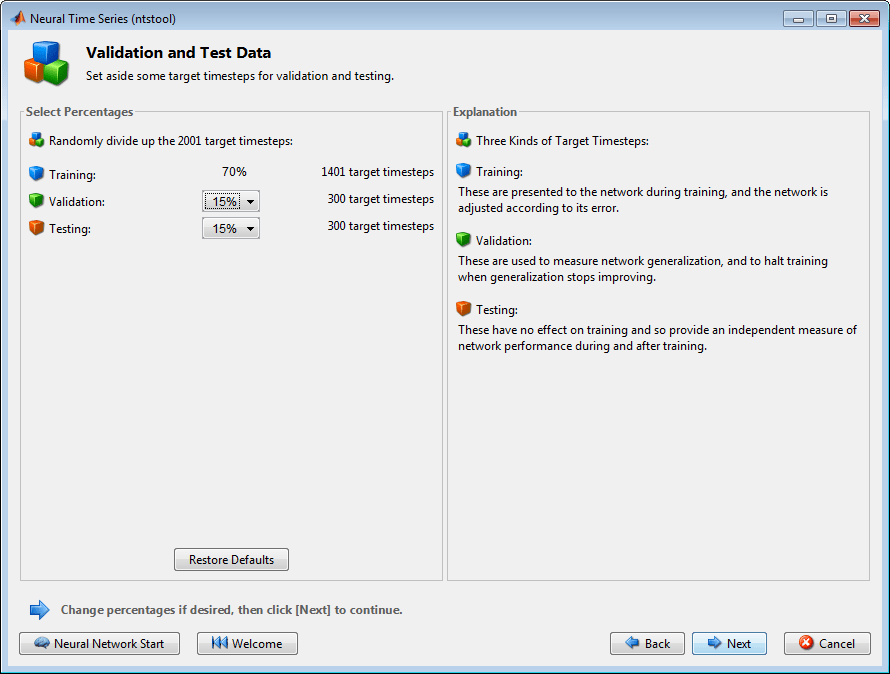
点击 Next 以打开 Validation and Test Data 窗口，如下图所示。

验证和测试数据集均设置为原始数据的 15%。

通过这些设置，输入向量和目标向量将随机分成如下三组：

70% 将用于训练。

15% 将用于验证网络是否正在泛化，并在过拟合前停止训练。

最后 15% 将用作网络泛化的完全独立测试。

(有关数据划分流程的更多讨论，请参阅划分数据。)

点击 Next。

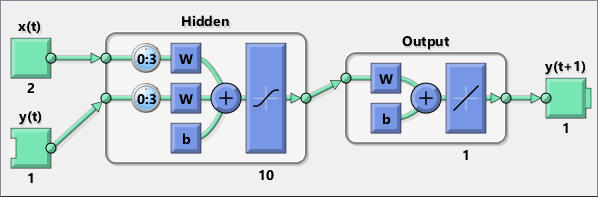
标准 NARX 网络是一个双层前馈网络，其中在隐藏层有一个 sigmoid 传递函数，在输出层有一个线性传递函数。该网络还使用抽头延迟线来存储 x(t) 和 y(t) 序列的先前值。您会注意到，NARX 网络的输出 y(t) 将(通过延迟)反馈给网络的输入，因为 y(t) 是 y(t – 1), y(t – 2), ..., y(t – d) 的函数。然而，为了有效训练，可以打开此反馈回路。

由于在网络训练期间真实输出是可用的，因此可以使用上面所示的开环架构，其中使用真实输出，而不是反馈估计输出。这样有两个优点。第一，前馈网络的输入更准确。第二，生成的网络为纯前馈架构，因此可以使用更高效的算法进行训练。NARX 网络(narxnet，closeloop)中更详细地讨论了该网络。

隐藏神经元的默认数量设置为 10。默认延迟数为 2。将该值更改为 4。如果网络训练性能不佳，您可能需要调整这些数字。

点击 Next。

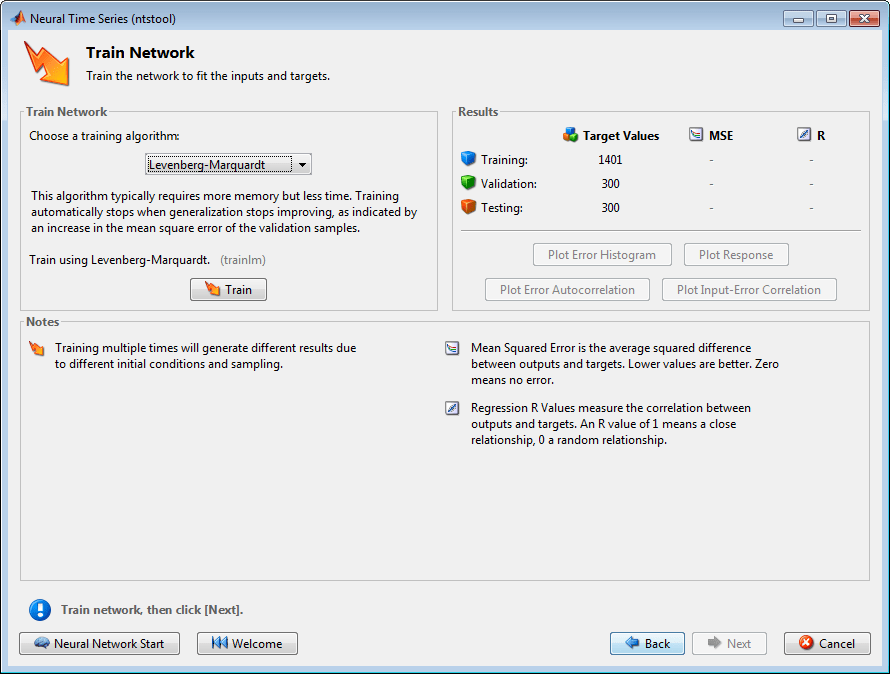
选择训练算法，然后点击 Train。对于大多数问题，推荐使用 Levenberg-Marquardt (trainlm)，不过，对于一些含噪小型问题，贝叶斯正则化 (trainbr) 虽然可能需要更长的时间，但会获得更好的解。但是，对于大型问题，推荐使用量化共轭梯度 (trainscg)，因为它使用的梯度计算比其他两种算法使用的 Jacobian 矩阵计算更节省内存。此示例使用默认的 Levenberg-Marquardt。

训练一直持续到连续六次迭代仍无法降低验证误差为止(验证停止)。

在 Plots 下，点击 Error Autocorrelation。这用于验证网络性能。

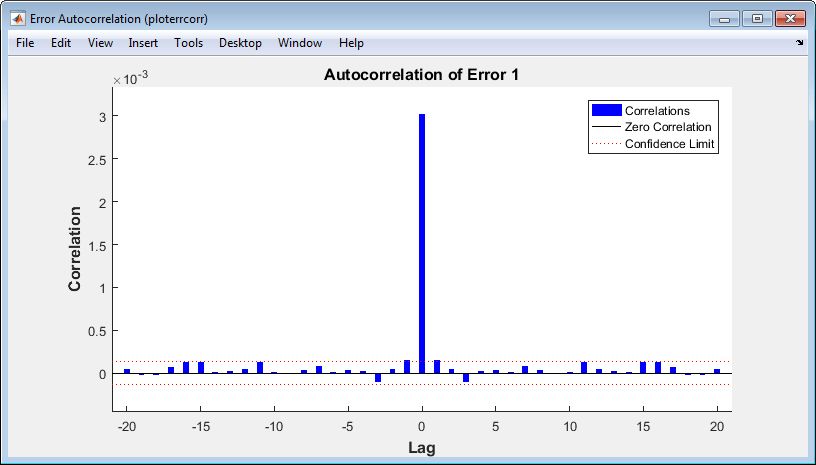
下图显示了误差自相关函数。它说明了预测误差在时间上是如何关联的。对于完美的预测模型，自相关函数应该只有一个非零值，并且应在零滞后时出现。(这是均方误差。)这表示预测误差彼此完全不相关(白噪声)。如果预测误差中存在显著相关性，则应该可以改进预测，这可以通过增加抽头延迟线中的延迟数量来实现。在这种情况下，除了零滞后时的 1 以外，相关性大约在零附近的 95% 置信界限范围内，因此模型看上去是足够的。如果需要更准确的结果，可以在 ntstool 中点击 Retrain 来重新训练网络。这将更改网络的初始权重和偏差，并可能在重新训练后生成改进的网络。

查看输入-误差互相关函数以获得网络性能的额外验证。在 Plots 窗格下，点击 Input-Error Cross-correlation。

该输入-误差互相关函数说明误差如何与输入序列 x(t) 相关。对于完美的预测模型，所有相关性都应为零。如果输入与误差相关，则应该可以改进预测，这可以通过增加抽头延迟线中的延迟数量来实现。在这种情况下，所有相关性都在零附近的置信边界范围内。

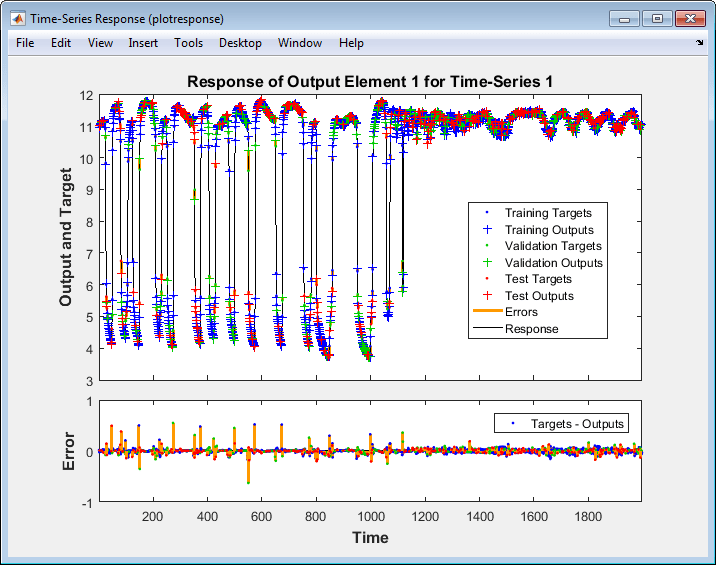
在 Plots 下，点击 Time Series Response。这将显示输入、目标和误差与时间的关系。它还指示选择了哪些时间点进行训练、测试和验证。

在 Neural Network Time Series 中点击 Next 以评估网络。

此时，您可以针对新数据测试网络。

如果您不满意网络对原始数据或新数据的性能，可以执行以下任一操作：

重新训练网络。

增加神经元的数量和/或延迟的数量。

获取更大的训练数据集。

如果网络对训练集的性能良好，但测试集的性能明显变差，这可能表示出现了过拟合，减少神经元数量可能会改善结果。

如果您对网络性能满意，请点击 Next。

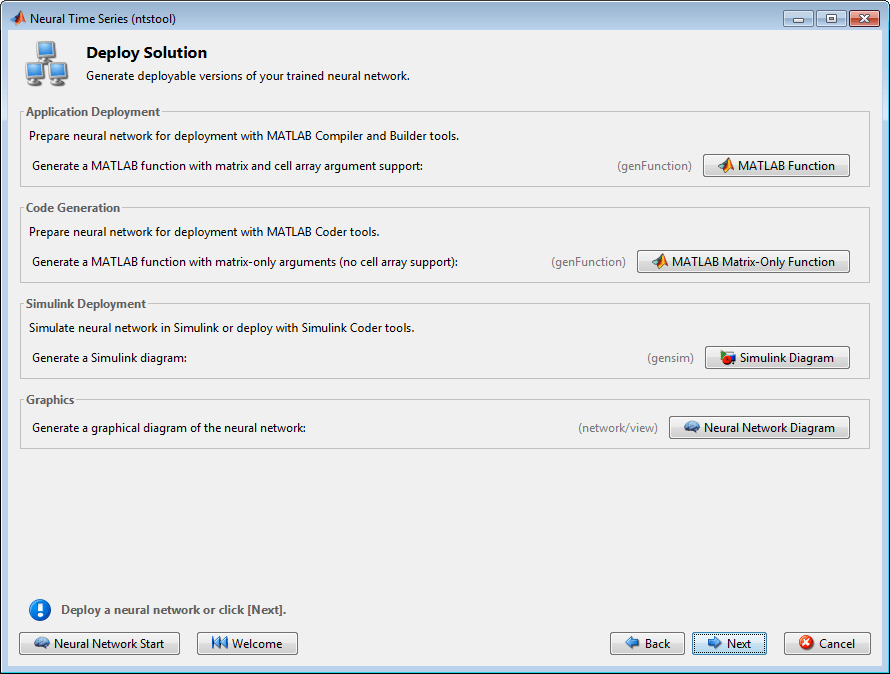
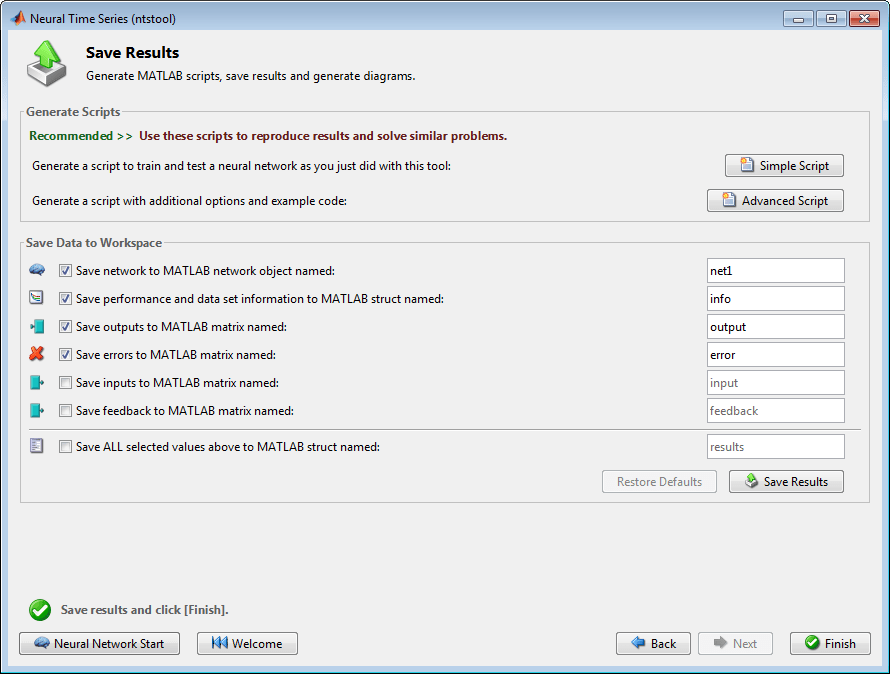
使用以下面板生成用于仿真您的神经网络的 MATLAB 函数或 Simulink® 图。您可以使用生成的代码或图来更好地理解您的神经网络如何根据输入计算输出，或使用 MATLAB Compiler™ 工具和其他 MATLAB 及 Simulink 代码生成工具来部署网络。

使用以下屏幕上的按钮生成脚本或保存结果。

您可以点击 Simple Script 或 Advanced Script 创建 MATLAB 代码，以通过命令行执行这些代码来重现前面的所有步骤。如果您要了解如何使用工具箱的命令行功能来自定义训练过程，则创建 MATLAB 代码会很有帮助。在使用命令行函数中，您可以更详细地研究生成的脚本。

您还可以将网络保存为工作区中的 net。您可以对它执行额外的测试，或让其处理新输入。

创建 MATLAB 代码并保存结果后，点击 Finish。使用命令行函数

了解如何使用工具箱的命令行功能的最简单方法是从 GUI 生成脚本，然后修改它们以自定义网络训练。例如，看一下在上一节的步骤 15 中创建的简单脚本。

% Solve an Autoregression Problem with External

% Input with a NARX Neural Network

% Script generated by NTSTOOL

%

% This script assumes the variables on the right of

% these equalities are defined:

%

% phInputs - input time series.

% phTargets - feedback time series.

inputSeries = phInputs;

targetSeries = phTargets;

% Create a Nonlinear Autoregressive Network with External Input

inputDelays = 1:4;

feedbackDelays = 1:4;

hiddenLayerSize = 10;

net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize);

% Prepare the Data for Training and Simulation

% The function PREPARETS prepares time series data

% for a particular network, shifting time by the minimum

% amount to fill input states and layer states.

% Using PREPARETS allows you to keep your original

% time series data unchanged, while easily customizing it

% for networks with differing numbers of delays, with

% open loop or closed loop feedback modes.

[inputs,inputStates,layerStates,targets] = ...

preparets(net,inputSeries,{},targetSeries);

% Set up Division of Data for Training, Validation, Testing

net.divideParam.trainRatio = 70/100;

net.divideParam.valRatio = 15/100;

net.divideParam.testRatio = 15/100;

% Train the Network

[net,tr] = train(net,inputs,targets,inputStates,layerStates);

% Test the Network

outputs = net(inputs,inputStates,layerStates);

errors = gsubtract(targets,outputs);

performance = perform(net,targets,outputs)

% View the Network

view(net)

% Plots

% Uncomment these lines to enable various plots.

% figure, plotperform(tr)

% figure, plottrainstate(tr)

% figure, plotregression(targets,outputs)

% figure, plotresponse(targets,outputs)

% figure, ploterrcorr(errors)

% figure, plotinerrcorr(inputs,errors)

% Closed Loop Network

% Use this network to do multi-step prediction.

% The function CLOSELOOP replaces the feedback input with a direct

% connection from the output layer.

netc = closeloop(net);

netc.name = [net.name ' - Closed Loop'];

view(netc)

[xc,xic,aic,tc] = preparets(netc,inputSeries,{},targetSeries);

yc = netc(xc,xic,aic);

closedLoopPerformance = perform(netc,tc,yc)

% Early Prediction Network

% For some applications it helps to get the prediction a

% timestep early.

% The original network returns predicted y(t+1) at the same

% time it is given y(t+1).

% For some applications such as decision making, it would

% help to have predicted y(t+1) once y(t) is available, but

% before the actual y(t+1) occurs.

% The network can be made to return its output a timestep early

% by removing one delay so that its minimal tap delay is now

% 0 instead of 1. The new network returns the same outputs as

% the original network, but outputs are shifted left one timestep.

nets = removedelay(net);

nets.name = [net.name ' - Predict One Step Ahead'];

view(nets)

[xs,xis,ais,ts] = preparets(nets,inputSeries,{},targetSeries);

ys = nets(xs,xis,ais);

earlyPredictPerformance = perform(nets,ts,ys)

您可以保存脚本，然后从命令行运行它，以重现上次 GUI 会话的结果。您还可以编辑脚本来自定义训练过程。在此例中，请执行脚本中的每个步骤。

脚本假设输入向量和目标向量已加载到工作区中。如果未加载数据，可以按如下方式加载它们：

load ph_dataset

inputSeries = phInputs;

targetSeries = phTargets;

创建一个网络。NARX 网络 narxnet 是一个前馈网络，其默认 tan-sigmoid 传递函数在隐藏层，线性传递函数在输出层。此网络有两个输入。一个是外部输入，另一个是来自网络输出的反馈连接。(完成网络训练后，可以关闭此反馈连接，详见后续步骤。)对于这些输入中的每一个，都有一条抽头延迟线来存储先前的值。要为 NARX 网络分配网络架构，您必须选择与每条抽头延迟线相关联的延迟，以及隐藏层神经元的数量。在后面的步骤中，您需要将输入延迟和反馈延迟的取值范围指定为 1 到 4，并将隐藏神经元的数量指定为 10。

inputDelays = 1:4;

feedbackDelays = 1:4;

hiddenLayerSize = 10;

net = narxnet(inputDelays,feedbackDelays,hiddenLayerSize);

注意

增加神经元数量和延迟数量需要更多计算，当数量设置得太高时，可能会出现数据过拟合倾向，但这也使得网络能够求解更复杂的问题。层越多，需要的计算也越多，但使用更多的层可以使网络更高效地求解复杂问题。要使用多个隐藏层，请在 fitnet 命令中输入隐藏层大小作为数组的元素。

准备用于训练的数据。当训练包含抽头延迟线的网络时，有必要用网络输入和输出的初始值来填充延迟。可以使用工具箱命令 preparets 来完成此过程。该函数有三个输入参数：网络、输入序列和目标序列。该函数返回填充网络中的抽头延迟线所需的初始条件，以及修改后的输入序列和目标序列(其中已删除初始条件)。您可以按如下方式调用该函数：

[inputs,inputStates,layerStates,targets] = ...

preparets(net,inputSeries,{},targetSeries);

设置数据划分。

net.divideParam.trainRatio = 70/100;

net.divideParam.valRatio = 15/100;

net.divideParam.testRatio = 15/100;

基于以上设置，输入向量和目标向量都将被随机划分为三组，其中 70% 用于训练，15% 用于验证，15% 用于测试。

训练网络。网络使用默认的 Levenberg-Marquardt 算法 (trainlm) 进行训练。对于 Levenberg-Marquardt 无法产生期望的准确结果的问题，或对于大型数据问题，请考虑使用以下命令之一将网络训练函数设置为贝叶斯正则化 (trainbr) 或量化共轭梯度 (trainscg)：

net.trainFcn = 'trainbr';

net.trainFcn = 'trainscg';

要训练网络，请输入：

[net,tr] = train(net,inputs,targets,inputStates,layerStates);

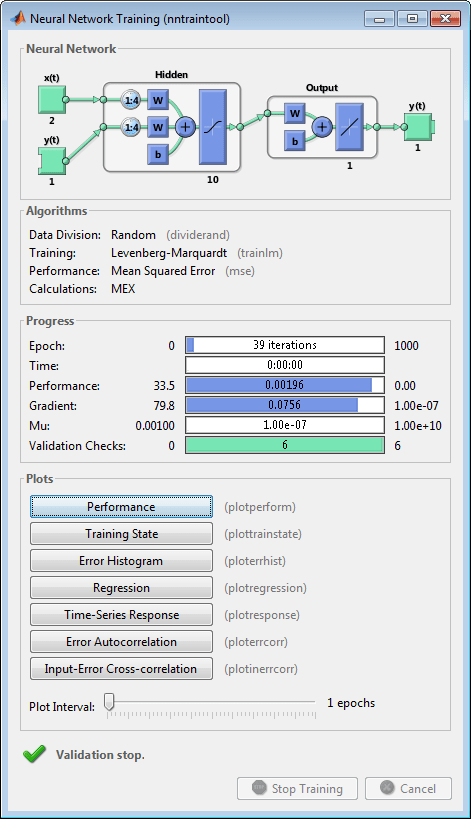
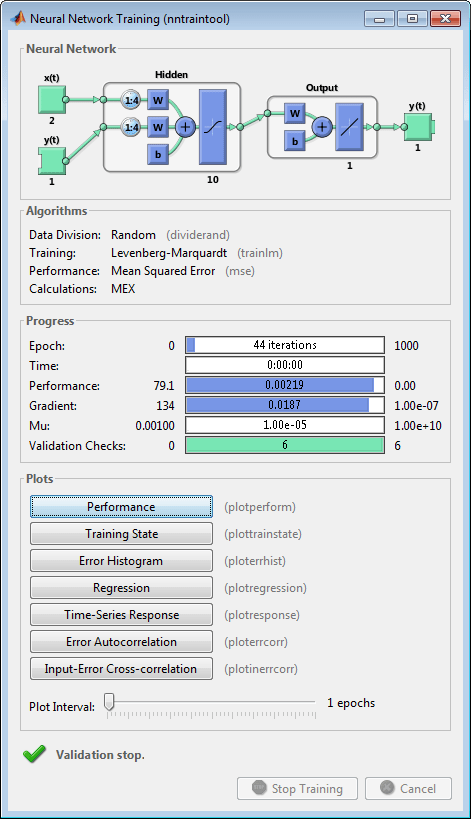
在训练期间，将打开以下训练窗口。此窗口显示训练进度，并允许您随时点击 Stop Training 来中断训练。

如果验证误差在六次迭代中持续增加，则训练将在第 44 次迭代时停止。

测试网络。您可以使用经过训练的网络来计算网络输出。以下代码将计算网络输出、误差和整体性能。请注意，要仿真具有抽头延迟线的网络，您需要为这些延迟信号指定初始值。这已在此前使用 preparets 提供的 inputStates 和 layerStates 完成。

outputs = net(inputs,inputStates,layerStates);

errors = gsubtract(targets,outputs);

performance = perform(net,targets,outputs)

performance =

0.0042

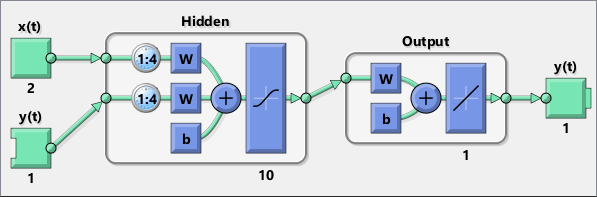
查看网络图。

view(net)

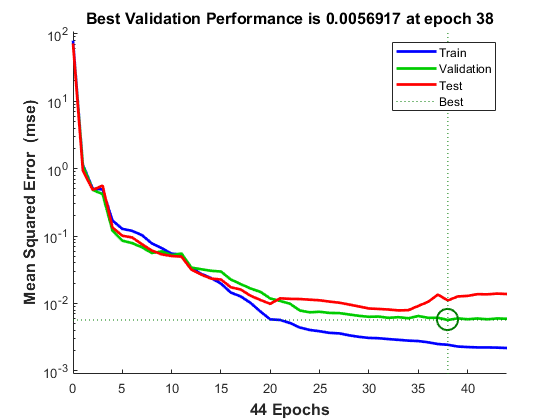
绘制性能训练记录以检查是否存在潜在过拟合。

figure, plotperform(tr)

此图显示，训练误差和验证误差一直在降低，直至突出显示的轮数处。图中并未显示发生了任何过拟合，因为验证误差在此轮之前没有增加。

所有训练以开环(也称为串并行架构)形式完成，包括验证和测试步骤。典型的工作流是完全以开环方式创建网络，并且仅当网络经过训练(包括验证和测试步骤)后，它才会变换为闭环，以进行向前多步预测。同样，GUI 中的 R 值是基于开环训练结果进行计算的。

闭合 NARX 网络上的回路。当 NARX 网络上的反馈回路处于打开状态时，它将执行一步超前预测。它根据 y(t) 和 x(t) 的先前值预测 y(t) 的下一个值。反馈回路闭合后，它可用于执行多步超前预测。这是因为 y(t) 的预测值将用于取代 y(t) 的实际将来值。以下命令可用于闭合回路和计算闭环性能

netc = closeloop(net);

netc.name = [net.name ' - Closed Loop'];

view(netc)

[xc,xic,aic,tc] = preparets(netc,inputSeries,{},targetSeries);

yc = netc(xc,xic,aic);

perfc = perform(netc,tc,yc)

perfc =

2.8744

从网络中删除一个延迟，以提前一个时间步获得预测。

nets = removedelay(net);

nets.name = [net.name ' - Predict One Step Ahead'];

view(nets)

[xs,xis,ais,ts] = preparets(nets,inputSeries,{},targetSeries);

ys = nets(xs,xis,ais);

earlyPredictPerformance = perform(nets,ts,ys)

earlyPredictPerformance =

0.0042

在此图中，您可以看到该网络与先前的开环网络相同，只是从每条抽头延迟线中删除了一个延迟。随后的网络输出是 y(t + 1)，而不是 y(t)。当为某些应用部署网络时，这可能会有所帮助。

如果网络性能不令人满意，您可以尝试以下任一方法：

使用 init 将初始网络权重和偏差重置为新值，然后再次训练(请参阅初始化权重 (init))。

增加隐藏神经元的数量或延迟的数量。

增加训练向量的数量。

增加输入值的数量(如果有更多相关信息可用)。

尝试其他训练算法(请参阅训练算法)。

要进一步熟悉命令行操作，请尝试以下任务：

在训练期间，打开绘图窗口(如误差相关图)，并观察其动画效果。

从命令行使用 plotresponse、ploterrcorr 和 plotperform 等函数绘图。(有关使用这些函数的详细信息，请参阅其参考页。)

此外，从命令行进行训练时，可以查看高级脚本以了解更多选项。

每次训练神经网络时，由于初始权重和偏置值不同，并且将数据划分为训练集、验证集和测试集的方式也不同，可能会产生不同的解。因此，针对同一问题训练的不同神经网络对同一输入可能给出不同输出。为确保找到准确度良好的神经网络，需要多次重新训练。

如果需要更高的准确度，可以采用几种其他方法来改进初始解。有关详细信息，请参阅提高浅层神经网络泛化能力，避免过拟合。