R2D2(NIPS 2019)特征点检测论文笔记
1.前言
论文地址
代码地址
文章基本是在 D2-Net 上做优化,作者提出了 Repeatable (重复性) 和 Reliable (可靠性) 两个属性对应 R2,个人理解重复性就是特征点在各种拍摄视角、光线、季节变化时依然能检测出来,可靠性就是描述符能正确匹配。作者认为之前的做法注重重复性,但是忽视了可靠性。

Figure 1: Toy examples to illustrate the key difference between repeatability (2nd column) and reliability (3rd column) for a given image. Repeatable regions in the first image are only located near the black triangle, however, all patches containing it are equally reliable. In contrast, all squares in the checkerboard pattern are salient hence repeatable, but are not discriminative due to self-similarity.
论文中的一个小实验,两组图像中间的关键点检测对应了可重复性,譬如第一组围绕三角形的周围,第二组棋盘的方块或者角点;右边的描述符可靠性对应可靠性,第一组包含三角形的 patches 同样可靠(特征对应的感受野都包含了这个三角形,所以特征都能正确匹配),第二组由于相似性没有区别(特征对应的感受野的图案非常相似,所以特征都一样没法正确匹配)。
作者认为在自然图像里面,常见的纹理,譬如树叶、大楼的窗、海浪等,他们的特征点突出,但是因为重复性和不稳定性,难以匹配。可重复区域不一定是有区别的 (repeatable regions are not necessarily discriminative),因此可以选次优的关键点。
其实感觉这个实验的力度不太够,最好是在自然图像上,表现出最优点匹配不如次优点。
2. 方法
2.1 网络结构
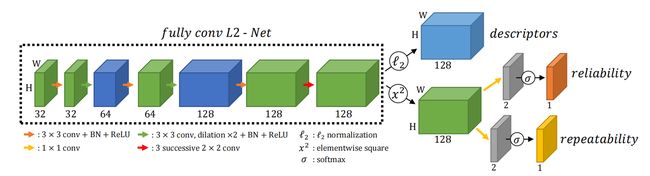
网络有三个输出:
(1) X ∈ R H × W × D \boldsymbol{X} \in \mathbb{R}^{H \times W \times D} X∈RH×W×D 对应描述符
(2) S ∈ [ 0 , 1 ] H × W \boldsymbol{S} \in [0,1]^{H \times W} S∈[0,1]H×W 对应特征点位置(重复性,后面个人取名为检测得分)
(3) R ∈ [ 0 , 1 ] H × W \boldsymbol{R} \in [0,1]^{H \times W} R∈[0,1]H×W 对应描述符的可靠性(后面个人取名为特征得分)
主干网络是 L2-Net,并作了两处修改:
(1)下采样的地方用扩展卷积替代了,每个阶段的特征图都保持了原图分辨率
(2)最后 8 × 8 8\times8 8×8 的卷积用 3个 2 × 2 2\times2 2×2 的卷积替代
主干网络的输出 128 维的特征图
(1)经过 L2 归一化得到每个像素的描述符 X \boldsymbol{X} X
(2)经过一个平方操作、 1 × 1 1\times1 1×1 卷积、softmax 得到 S \boldsymbol{S} S
(3)经过和(2)一样的操作得到 R \boldsymbol{R} R
2.2 重复性(检测得分)
作者表示一些监督训练(Lift、SuperPoint)是无法解决重复性问题的,因为他们都是模仿现有的检测器,而不是发现潜在的更好的关键点。
对图像 I I I 做一个单应性变换得到 I ′ I^\prime I′,这样就有了每个像素精确的对应关系 U ∈ R H × W × 2 U \in \mathbb{R}^{H \times W \times 2} U∈RH×W×2, U i j = ( i ′ , j ′ ) U_{i j}=\left(i^{\prime}, j^{\prime}\right) Uij=(i′,j′) 代表 I I I 中的像素 ( i , j ) (i,j) (i,j) 与 I ′ I^\prime I′ 中的像素 ( i ′ , j ′ ) \left(i^{\prime}, j^{\prime}\right) (i′,j′) 对应; I , I ′ I,I^\prime I,I′ 的检测得分为 S , S ′ S,S^\prime S,S′, S ′ S^\prime S′ 按 U U U 做变换得到 S U ′ S^\prime_U SU′。
目标是让 S S S 和 S U ′ S^\prime_U SU′ 的局部极大值对上,如直接最大化两者的余弦相似度,但是在实践中因为各种遮挡、伪影等等情况使用这种方法不现实。因此选择计算一个局部区域余弦相似度的均值,将检测得分图所有大小为 N × N N \times N N×N 的可重叠 patches 作为一个集合 P = { p } \mathcal{P}=\{p\} P={p}
L cosim ( I , I ′ , U ) = 1 − 1 ∣ P ∣ ∑ p ∈ P cosim ( S [ p ] , S U ′ [ p ] ) \mathcal{L}_{\operatorname{cosim}}\left(I, I^{\prime}, U\right)=1-\frac{1}{|\mathcal{P}|} \sum_{p \in \mathcal{P}} \operatorname{cosim}\left(\boldsymbol{S}[p], \boldsymbol{S}_{U}^{\prime}[p]\right) Lcosim(I,I′,U)=1−∣P∣1p∈P∑cosim(S[p],SU′[p])
为了不让得分变得全都一样,用了一个损失来最大化局部峰值:
L peaky ( I ) = 1 − 1 ∣ P ∣ ∑ p ∈ P ( max ( i , j ) ∈ p S i j − mean ( i , j ) ∈ p S i j ) \mathcal{L}_{\text {peaky }}(I)=1-\frac{1}{|\mathcal{P}|} \sum_{p \in \mathcal{P}}\left(\max _{(i, j) \in p} \boldsymbol{S}_{i j}-\operatorname{mean}_{(i, j) \in p} \boldsymbol{S}_{i j}\right) Lpeaky (I)=1−∣P∣1p∈P∑((i,j)∈pmaxSij−mean(i,j)∈pSij)
最终的检测得分损失:
L rep ( I , I ′ , U ) = L cosim ( I , I ′ , U ) + 1 2 ( L peaky ( I ) + L peaky ( I ′ ) ) \mathcal{L}_{\text {rep }}\left(I, I^{\prime}, U\right)=\mathcal{L}_{\text {cosim }}\left(I, I^{\prime}, U\right)+\frac{1}{2}\left(\mathcal{L}_{\text {peaky }}(I)+\mathcal{L}_{\text {peaky }}\left(I^{\prime}\right)\right) Lrep (I,I′,U)=Lcosim (I,I′,U)+21(Lpeaky (I)+Lpeaky (I′))
N N N 不同的取值效果如下:
2.3 可靠性(特征得分)
这里论文说到了,特征得分 R R R 的作用是提高描述符之间的区别,或者避免在天空或地面这种平坦区域检测出特征点。
I I I 中每一个像素 ( i , j ) (i,j) (i,j) 都是一个 M × M M \times M M×M 的 patch p i j p_{ij} pij 的中心,其描述符为 X i j \boldsymbol{X}_{ij} Xij,可以和 I ′ I^\prime I′ 所有 patches 的描述符 { X u v ′ } \{\boldsymbol{X}^\prime_{uv}\} {Xuv′} 作比较。已知 U U U,所以可以用 AP(平均精度)来估计 p i j p_{ij} pij 的可靠性。按一篇论文对 AP 进行优化得到一个可求导的近似,记作 A P ~ \widetilde{\mathrm{AP}} AP 。 B B B 代表一个 batch 中 patch 的数量。
L A P = 1 B ∑ i j 1 − A P ~ ( p i j ) \mathcal{L}_{A P}=\frac{1}{B} \sum_{i j} 1-\widetilde{\mathrm{AP}}\left(p_{i j}\right) LAP=B1ij∑1−AP (pij)
虽然每个像素都提取了描述符,但并不是每个都适合作为特征点,通常平滑区域不太好,但事实上纹理丰富的地方也不一定好,所以修改了下 loss,让网络关注次优的区域。
L A P , R = 1 B ∑ i j 1 − A P ~ ( p i j ) R i j + κ ( 1 − R i j ) \mathcal{L}_{A P, \boldsymbol{R}}=\frac{1}{B} \sum_{i j} 1-\widetilde{\mathrm{AP}}\left(p_{i j}\right) \boldsymbol{R}_{i j}+\kappa\left(1-\boldsymbol{R}_{i j}\right) LAP,R=B1ij∑1−AP (pij)Rij+κ(1−Rij)
κ ∈ [ 0 , 1 ] \kappa \in [0,1] κ∈[0,1],代表是否可靠的 AP 阈值,取0.5效果较好。这里论文说了一堆分析也没太看明白,个人从这个 loss 公式分析,为了让 loss 降低,其实每个点都会想让 A P ~ \widetilde{\mathrm{AP}} AP 和 R \boldsymbol{R} R 升高,这里 A P ~ \widetilde{\mathrm{AP}} AP 的计算方式不看代码也不清楚细节,就当做匹配的效果或者说是匹配的难易程度。当 A P ~ \widetilde{\mathrm{AP}} AP 较高,意味着特征明显、容易匹配、匹配的很正确,那么网络就会更倾向于拉高这个点的 R \boldsymbol{R} R,可靠性越高,符合逻辑。这就可以实现有些点的检测得分高,纹理特征强,但是因为匹配难度高,降低它的特征得分。
(2022.1.21)写论文梳理时看了一下代码发现这边可靠性得分的损失应该是写错了,return 1 - ap*rel - (1-rel)*self.base,可以看出这边的加号应该是减,也解决了之前的困惑。这样也才更符合逻辑,当 A P ~ \widetilde{\mathrm{AP}} AP 小于0.5时降低可靠性得分;假如是加号,训练会很麻烦,只能训练到一半,依赖梯度下降速度得到相对可靠的得分,彻底训练的话得分应该都是1。
3. 个人总结
(1)D2-Net 的损失是以特征匹配为主,加个检测得分的相关项作为权重;而 R2D2 专为检测得分设计了一个损失,也就是局部的得分和对应局部的得分要相似,拉开局部最大值和均值差距作为正则化。
(2)特征得分的思路是用实际的特征匹配效果来收敛;假如一个区域平滑没啥特征,网络也整不出特立独行的特征,匹配也自然效果不好,这时匹配度就低;假如一个区域纹理丰富,网络是能整点有特色的特征,但是有类似这个特征的地方太多了(开头的树叶、大楼的窗、海浪等),这样匹配也难度比较高,就不作为特征点了;这样就能让网络得到又有特征(几何信息丰富),又有特点(在图像中重复性低,很有特色容易匹配)的特征点。