图解机器学习中的张量

图解张量(tensor)

张量是什么？本讲的目的是回答这个问题，不是用一堆数学方程，用一些简单的家用物品，包括儿童积木、小箭头、几块纸板和一根尖头棒。我认为理解张量的最佳途径是首先确保你对向量的理解是扎实的。

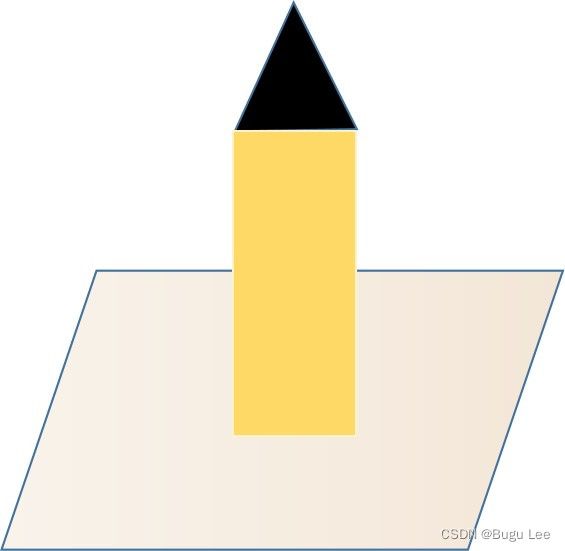
向量是表示同时具有大小和方向的量，其中箭头的长度与量的大小成比例，箭头的方向告诉您量的方向。这可以表示物体的重力，或地球磁场的强度和方向，或流动流体中粒子的速度。但向量也可以表示其他事物，例如面积。

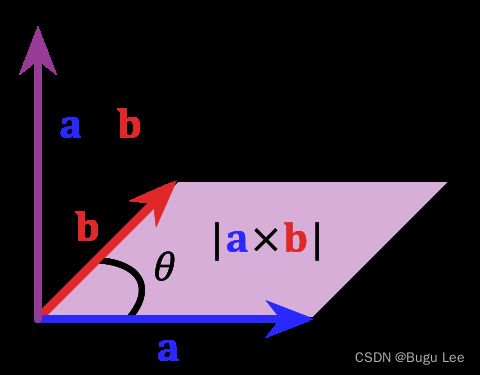
只需使向量的长度与面积（面积中的平方米数）成比例，然后使箭头的方向垂直于曲面。理解向量的叉乘就很容易理解用向量表示面积。

因此，这样也可以表示一个区域。所以向量可以代表很多东西。但是，如果除了把向量理解为表示数量的大小和方向的量，把向量理解为一类更广泛的称为张量的对象的成员，那么必须确保你理解向量分量和基向量，即向量的组成部分。

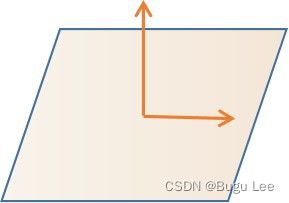
上图是笛卡尔坐标系(Cartesian coordinate system)。 关于坐标系，需要记住的是，它们与坐标基向量一起出现，如下：

单位向量的长度是1，1表示要表达向量长度的任何单位之一。基向量或单位向量的方向是坐标轴的方向，因此这可能表示x方向上的单位向量 $\hat{x}$ 或 $\hat{i}$ 。一旦有了坐标系和单位向量，就可以找到向量的分量。

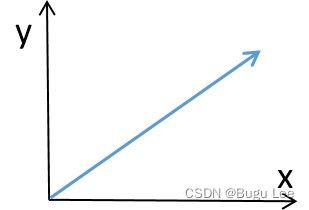
如果你从（x，y）平面上的向量开始。为了找到x分量，我将把这个向量投影到x轴上。为了找到y分量，我将把这个向量投影到y轴上。如果我使向量与x轴成更大的角度，请注意x分量越来越小，y分量越大。如果我让向量完全沿着x轴，那么阴影和向量的长度是相同的，在这种情况下，x分量就是向量的长度。

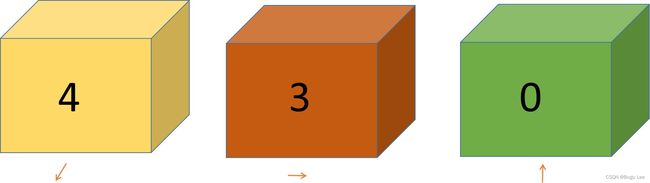
从向量的底端到向量的顶端，在x方向走多远，在y方向走多远？换言之，从这个向量的基部到顶端需要多少个x方向的单位向量（$\hat{x}$ 或 $\hat{i}$ ）和多少个y方向的单位向量（$\hat{y}$ 或 $\hat{j}$ ）？这个向量由四个 $\hat{x}$ 加上三个 $\hat{y}$ 组成, 即 $4\hat{x}$ + $3\hat{y}$ 。

如果知道了基向量，这意味着不用为这个向量画箭头（基向量），你可以简单地说四个，再加上三个。如果加上z方向（因为这个向量没有z分量），z方向为0。换句话说，如果你知道基向量，用4，3，0这三个分量来表示该向量的一个完全有效的表示。

可以简单地使用这些分量作为向量。你可以把它写成一个小数组。如上图所示，甚至可以将它们堆叠起来，并在其周围加一组括号。这就像写列向量的方式。

当然，这三个分量只与前面讲的那个向量有关。为了将其推广到一般的向量A，可以将这些分量替换为Ax、Ay和Az。

在这里插入图片描述

当然，Ax是属于 $\hat{x}$ 基向量的分量，Ay是属于$\hat{y}$ 基向量的分量，Az是属于$\hat{z}$ 基向量的分量。注意，需要为每一个分量创建一个指针（index），因为每个分量只有一个方向指示器（即一个基向量）。这就是向量是“秩为一的张量(tensors of rank one)”的原因，一个指针，或每个分量一个基向量。同样，标量可以被看作零阶张量，因为标量没有方向指示器，因此不需要指针，这是零阶张量。马上就会明白为什么将张量表示为分量和基向量的组合如此强大，首先来看一些高阶张量的示例。

注：这里的指针(index)不是编程里面的指针，而是指明方向的单位向量，在坐标系中就是基向量。

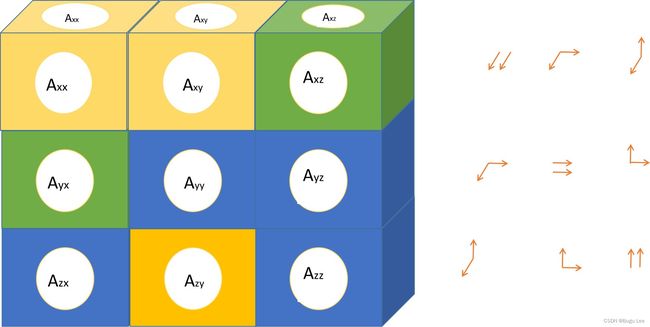
如上图所示，这是三维空间中二阶张量的表示。注意，现在没有三个分量和三个基向量，而是有九个分量和九组两个基向量。还请注意，分量不再具有单个指针，而是具有两个指针。为什么需要这样的表示呢？

例如，考虑实体对象内部的力。在该对象内部，可以想象其面积向量指向x、y或z方向的曲面。在每一种类型的表面上，都可能有一个力，它的分量在x方向，或者在y方向，或者在z方向。因此，要充分描述所有可能曲面上的所有可能力，需要九个分量，每个分量都有两个指针表示基向量。例如，Axx可能指的是面积向量在x方向的曲面上的x方向力，Ayx可能指的是面积向量在y方向的曲面上的x方向力，依此类推。九个分量和九组两个基向量的组合使其成为二阶张量。

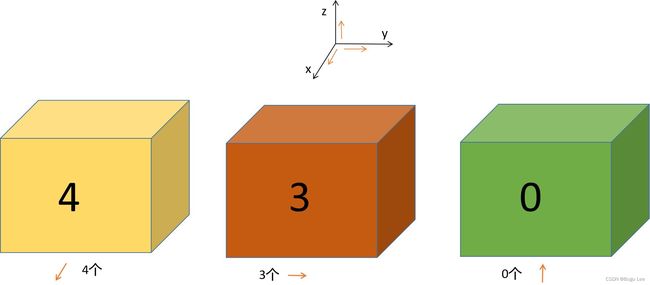
上图是三维27个分量中三阶张量的表示，每个分量属于27组三个基向量中的一组。向量，Axyx属于两个x和一个y基向量，依此类推。整个前面板的第三个索引为x，属于这九组基本向量。中间的板都有y作为第三个索引，并且属于这九个，后面的面板都有z作为第三个索引，并且属于这九个。所以在三维空间中有27个分量，27组三个基向量，每个分量上有三个指针。为什么分量和基向量的组合让张量如此强大？答案是，在所有参考系中，所有观察者都同意这一点，不是在基础向量上，而是在分量和基向量的组合上。其原因是，基向量在参考帧之间以一种方式变换，而分量以这种方式变换，以便保持所有观察者的分量和基向量的组合相同。正是张量的这一特性使得Lillian Lieber将张量称为“宇宙的事实(the facts of the universe)”。

A tensor is something that transforms like a tensor! 一个量, 在不同的参考系下按照某种特定的法则进行变换, 就是张量. 【本句出自：什么是张量 (tensor)？ - andrew shen的回答 - 知乎】

Reference:

1. https://www.youtube.com/watch?v=f5liqUk0ZTw