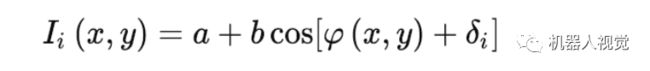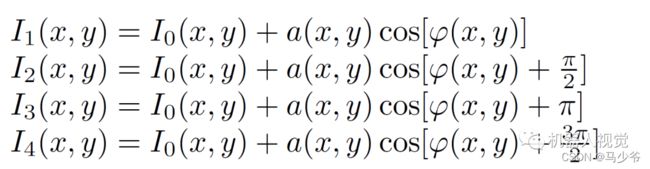结构光多频外差法原理和代码
1、相移法原理
结构光法原理其实是跟双目视觉一样的,都是要确定对应“匹配点”,利用“视差”三角关系计算距离,所不同的是:
双目视觉通过“被动”匹配唯一特征点
相移法作为结构光法中的一种,通过主动投影多副相移图案来标记唯一位置。虽然大多数结构光系统是单目的,但我们可以将其“双目”的,因为投影仪可以看做是一个“逆向”的相机,明白了这点,对于结构光系统一些公式推导就容易很多。
对于“双目”系统来说,最重要的工作是通过唯一标记来标记某一点,假设我们只投射一个周期的数据,我们从投影仪投出去的光栅公式如下:
其中:
比如说四步相移公式:
需要说明的是,虽然这个公式对整副相移图像的,但是这公式对每个像素都是独立的,所以即使我们拿从相机拍摄到经过调制变形的图像来求解,依然可以得到单个像素点唯一的相位主值。
我们主要关心的是求解出相位主值,因为它对每个像素点是唯一的,假设我们从相机中获取了这四副图像,那怎么反过来求解相位主值?
联立4个方程,得到:
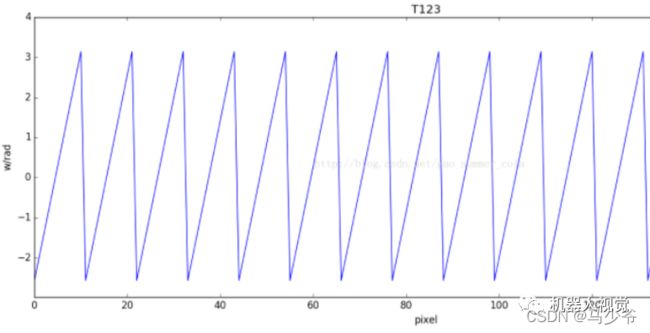
无论拍摄到什么图像,我们要得到某个像素点的唯一“标记”,也就是这个相位主值,代回这个公式即可,都可以得到唯一值。得到了唯一值,建立匹配关系,就可以利用三角公式进行重建。
其中:横坐标为任意一行的像素,这张图中使用周期为11的像素条纹作为正弦光栅。
2、双频外差原理
解决的方法有很多,分为空域和时域展开两种:
空域展开:依靠空间相邻像素点之间的相位值恢复绝对相位,如果重建表面不连续,则出现解码错误。
时域展开:将每个像素点的相位值进行独立计算,有格雷码和多频外差两种,其中格雷码方法对物理表面问题敏感,并且多投影的图并不能用来提升精度,多频外差精度更高。
当然目前还有更多精度更高、效率更快的相位展开方法,在这里暂时不予讨论,这里主要讨论多频外差原理。
多频外差原理:通过多个不同频率(周期)正弦光栅的相位做差,将小周期的相位主值转化为大周期的相位差,从而使得相位差信号覆盖整个视场,然后再根据相位差来得到整副图像的绝对相位分布。
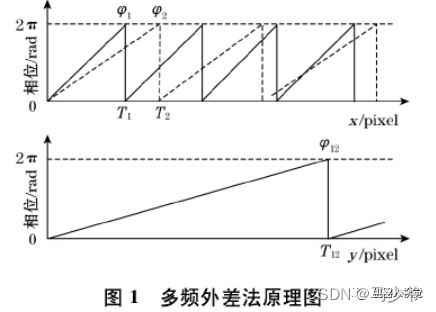
这里以双频外差为例,原理如图1所示:
通常我们说的相位函数的周期,代表的是一个周期正弦函数所占的像素单位个数。
从上述公式可以看出,我们使用两种不同周期的相位值叠加得到一种周期更长的相位函数,为了能够利用多频外差原理实现全场无歧义的相位展开,我们必须选择合适的T1和T2,使得T12能够超过整个视场,从而获得唯一的相位。
其可以完成整个视场的无歧义标记。
依据相移法得到的包裹相位图如下图所示,不同颜色代表不同频率的相位主值:
我们进行叠加后的效果:
在这里,我们可以看到,由两个周期小的相位可以合成一个周期更大的编码图案。
其中:
明白了原理,我们来代码实践一下,需要注意的是,求解出来的相位我们要进行归一化到区间操作:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def phase_simulation(WIDTH, T1, T2, T3):
pha1, pha2, pha3 = np.zeros(shape=WIDTH), np.zeros(shape=WIDTH), np.zeros(shape=WIDTH)
t1, t2, t3 = 1, 1, 1
for idx in range(WIDTH):
if t1 > T1: t1 = 1 # 重置一下
pha1[idx] = (t1 / T1) * 2 * np.pi
if t2 > T2: t2 = 1
pha2[idx] = (t2 / T2) * 2 * np.pi
if t3 > T3: t3 = 1
pha3[idx] = (t3 / T3) * 2 * np.pi
t1 += 1; t2 += 1; t3 += 1
return pha1, pha2, pha3
def parse_phase(pha1, pha2, T1, T2):
pha12 = np.zeros_like(pha1)
# 计算Delta(如果满足条件,输出左侧,否则右侧)
pha12 = np.where(pha1 >= pha2, pha1 - pha2, pha1 - pha2 + 2 * np.pi)
# # 跟下面这段代码等价
# for idx in range(0, pha12.shape[0]):
# if pha1[idx] >= pha2[idx]:
# pha12[idx] = pha1[idx] - pha2[idx]
# else:
# pha12[idx] = pha1[idx] - pha2[idx] + 2 * np.pi
T12 = T1 * T2 / (T2 - T1)
# 方法1
pha12 = T2 / (T2 - T1) * pha12
# # 方法2
# m = np.round((T2 / (T2 - T1) * pha12 - pha1) / (2 * np.pi))
# pha12 = 2 * np.pi * m + pha12
# 归一化到[0,2π]
min_value, max_value = np.min(pha12), np.max(pha12)
pha12 = (pha12 - min_value) * (2 * np.pi / (max_value - min_value))
return pha12, T12
if __name__ == '__main__':
# 视场宽度
WIDTH = 854
# 条纹周期
T1 = 11
T2 = 12
T3 = 13
pha1, pha2, pha3 = phase_simulation(WIDTH, T1, T2, T3)
X = np.arange(0, WIDTH)
plt.plot(X, pha1, label="pha1")
plt.plot(X, pha2, label="pha2:")
plt.plot(X, pha3, label="pha3")
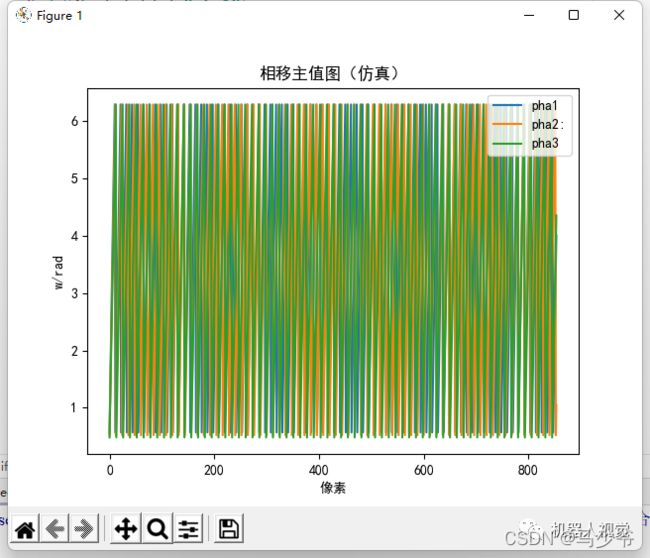
plt.title("相移主值图(仿真)")
plt.xlabel("像素")
plt.ylabel("w/rad")
plt.legend()
plt.show()
# 解相位
pha12, T12 = parse_phase(pha1, pha2, T1, T2)
pha23, T23 = parse_phase(pha2, pha3, T2, T3)
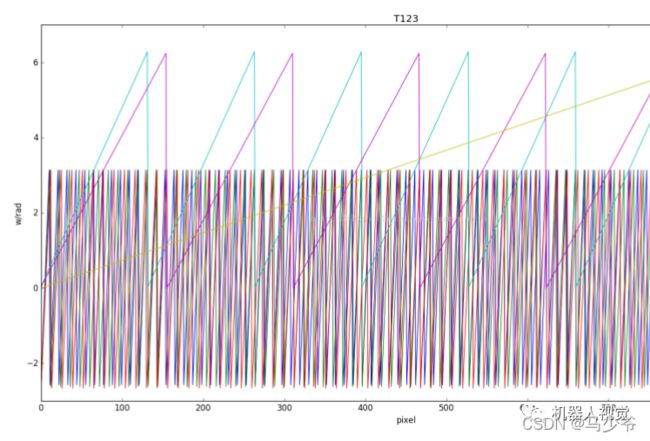
pha123, T123 = parse_phase(pha12, pha23, T12, T23)
plt.plot(X, pha12, label="pha12")
plt.plot(X, pha23, label="pha23")
plt.plot(X, pha123, label="pha123")
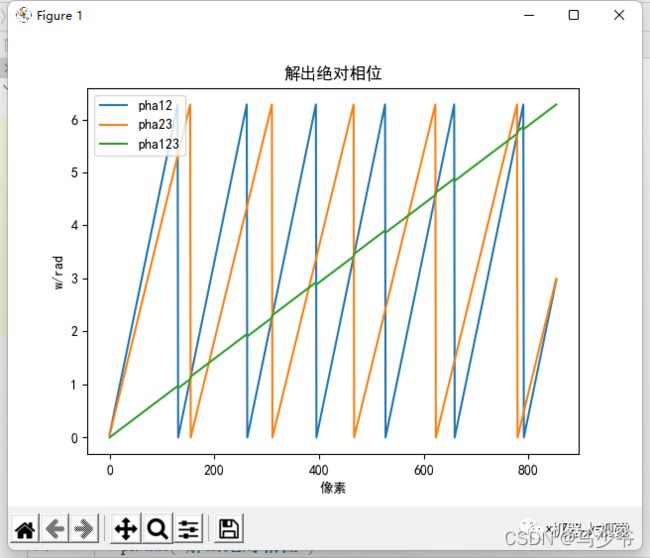
plt.title("解出绝对相位")
plt.xlabel("像素")
plt.ylabel("w/rad")
plt.legend()
plt.show()
测试结果如下:
可以看出,最终解出的绝对相位线单调递增,每个相位值是唯一的,虽然在一些交界处会有些许误差。结构光多频外差的原理很简单,而精度这块,其实很大程度依赖于标定、高反处理这些地方。