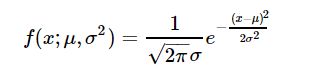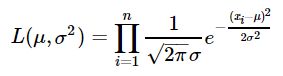机器学习之极大似然估计

一、什么是极大似然估计？

1.首先来看贝叶斯分类，我们都知道经典的贝叶斯公式：


2.在日常生活中，我们很容易无意中就使用到极大似然估计的思想，只是我们并不知道极大似然估计在数学中的如何确定以及推导的。下面我们使用两个例子让大家大概了解一下什么是极大似然估计：

• （1）猎人师傅和徒弟一同去打猎，遇到一只兔子，师傅和徒弟同时放枪，兔子被击中一枪，那么是师傅打中的，还是徒弟打中的？
• （2）一个袋子中总共有黑白两种颜色100个球，其中一种颜色90个，随机取出一个球，发现是黑球。那么是黑色球90个？还是白色球90个？
• 对于第（1）个问题，由于师傅的技术一般比徒弟高，因此我们会猜测兔子是师傅打中的。对于第（2）个问题，对于颜色有90个的球，我们抽中它的概率更大，因此当抽中为黑色球时，我们便会认为90个的是黑色球。
• 对于以上两个例子可以看出，我们在进行猜测时，往往认为：概率最大的事件，最可能发生，因此在一次试验中就出现的事件应当具有较大的概率。

二、极大似然原理及数学表示

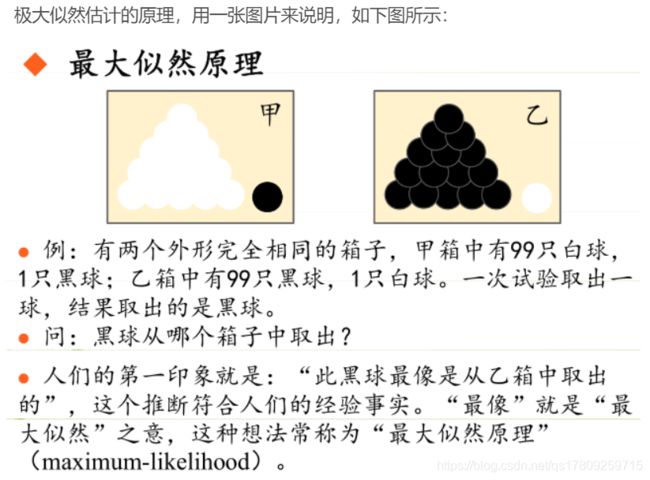
1.极大似然原理

• 总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
• 原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计
  
  2.极大似然估计

在一次抽样中，样本出现的概率是关于参数 θ 的函数，若在一些试验中，得到观测值$x_1,x_2,...,x_n$，则我们可以选取θ^$(x_1,x_2,...,x_n)$，作为 θ 的估计值，使得当 θ=θ^$(x_1,x_2,...,x_n)$时，样本出现的概率最大。而极大似然估计就是要求解出参数 θ 的估计值。可采用极大似然估计法。

三、极大似然估计法(Maximum Likelihood Estimation,MLE)

（1）若总体 X 为离散型
    
（2）若总体 X 为连续型
    

四、 极大似然估计法求估计值的步骤：

五、极大似然估计法应用

（1）假设一个袋子装有白球与红球，比例未知，现在抽取10次（每次抽完都放回，保证事件独立性），假设抽到了7次白球和3次红球，在此数据样本条件下，可以采用最大似然估计法求解袋子中白球的比例。
求解过程：

• 该试验属于二项分布，我们定义 M 为模型，抽到白球的概率为 θ ，而抽到红球的概率为 1−θ
  ，因此10次抽取抽到白球7次红球3次的概率(似然函数)为：

• 其对数似然函数为:

• 求

• 即：

二项式系数为常数，在求导过程中会被抵消。故白球的比例为 0.7 。
    
(2）设总体 $XN(\mu ,\sigma 2)，\mu ,\sigma 2$ 为未知参数，$x_1,x_2,...,x_n$是来自 X 的一个样本值，求$\mu ,\sigma 2$ 的极大似然估计值。

求解过程：

• X的概率密度为：

• 似然函数为：

• 取对数为：

• 令：

• 即：

• 求得参数估计值为：

六、总结

求最大似然估计量的一般步骤：

1. 写出似然函数；
2. 对似然函数取对数，并整理；
3. 求导数；
4. 解似然方程。

最大似然估计的特点：

1. 比其他估计方法更加简单；
2. 收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；
3. 如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计结果。

参考：https://blog.csdn.net/zengxiantao1994/article/details/72787849
https://www.cnblogs.com/lliuye/p/9139032.html