神经网络与深度学习作业7-第五章课后题（1×1 卷积核 | CNN BP）

---

习题5-2 证明宽卷积具有交换性。

习题5-3 分析卷积神经网络中用1×1的卷积核的作用。

作用1：降维(减少参数) or 升维(用最少的参数拓宽网络channal)

一、降维
加入1*1的卷积核可以通过减少通道数来减少参数，同样通过减少通道数来进行数据的降维处理。
例如现在有一个图像大小为$M\ast N\ast D$，即图片大小为$M\ast N$，通道数为$D$，我们通过$1\ast 1$的卷积核进行卷积，可以得到$M\ast N$的结果，从而达到降维的目的。
二、升维

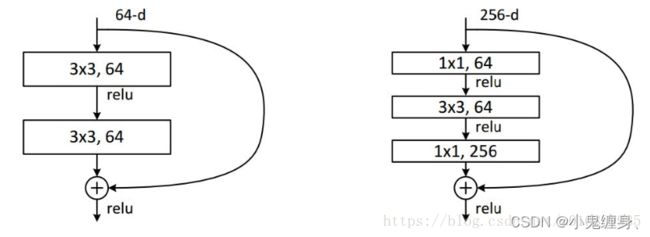
上图中，在输入处有一个$1\ast 1$卷积核，在输出处也有一个卷积核，$3\ast 3$，$64$的卷积核的channel是$64$，只需$3\ast 3$卷积层后添加一个$1\ast 1$，$256$的卷积核，只用$64\ast 256$个参数就能把网络 channel 从 $64$ 拓宽四倍到 $256$。

假定上一层的feature map是wh256,并且最后要输出的是256个channel。

左图中结构的操作数：$w\ast h\ast 256\ast 3\ast 3\ast 256=589824\ast w\ast h$

左图中结构侧操作数：$w\ast h\ast 256\ast 1\ast 1\ast 64+w\ast h\ast 64\ast 3\ast 3\ast 64+w\ast h\ast 64\ast 1\ast 1\ast 256=69632\ast w\ast h$，右图参数大概是左图参数八分之一。

作用2：增加深度

每使用 $1x1$卷积核，及增加一层卷积层，所以网络深度得以增加。 而使用$ 1x1$卷积核后，可以保持特征图大小与输入尺寸相同，卷积层卷积过程会包含一个激活函数，从而增加了非线性。在输入尺寸不发生改变的情况下而增加了非线性，所以会增加整个网络的表达能力。

习题5-4 对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度。

第一问：
$TimeO(M^2\ast K^2\ast C_{in}\ast C_{out})$:256×100×100×256×3×3 = 5,898,240,000
$SpaceO(M^2\ast K^2\ast C_{in}\ast C_{out}$：256×100×100 = 2,560,000
第二问：
$TimeO(M^2\ast K^2\ast C_{in}\ast C_{out})$：64×100×100×256 + 256×100×100×64×3×3 = 1,638,400,000
$SpaceO(M^2\ast K^2\ast C_{in}\ast C_{out}$：64×100×100 + 256×100×100 = 3,200,000

习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系。

附加1：CNN反向传播推导。

附加2：设置简易CNN模型，分别用Numpy和Pytorch实现卷积层和池化层的反向传播算子，并带入数值测试。

卷积反向传播实现：

from typing import Dict, Tuple

import numpy as np
import pytest
import torch


def conv2d_forward(input: np.ndarray, weight: np.ndarray, bias: np.ndarray,
                   stride: int, padding: int) -> Dict[str, np.ndarray]:
    """2D Convolution Forward Implemented with NumPy

    Args:
        input (np.ndarray): The input NumPy array of shape (H, W, C).
        weight (np.ndarray): The weight NumPy array of shape
            (C', F, F, C).
        bias (np.ndarray | None): The bias NumPy array of shape (C').
            Default: None.
        stride (int): Stride for convolution.
        padding (int): The count of zeros to pad on both sides.

    Outputs:
        Dict[str, np.ndarray]: Cached data for backward prop.
    """
    h_i, w_i, c_i = input.shape
    c_o, f, f_2, c_k = weight.shape

    assert (f == f_2)
    assert (c_i == c_k)
    assert (bias.shape[0] == c_o)

    input_pad = np.pad(input, [(padding, padding), (padding, padding), (0, 0)])

    def cal_new_sidelngth(sl, s, f, p):
        return (sl + 2 * p - f) // s + 1

    h_o = cal_new_sidelngth(h_i, stride, f, padding)
    w_o = cal_new_sidelngth(w_i, stride, f, padding)

    output = np.empty((h_o, w_o, c_o), dtype=input.dtype)

    for i_h in range(h_o):
        for i_w in range(w_o):
            for i_c in range(c_o):
                h_lower = i_h * stride
                h_upper = i_h * stride + f
                w_lower = i_w * stride
                w_upper = i_w * stride + f
                input_slice = input_pad[h_lower:h_upper, w_lower:w_upper, :]
                kernel_slice = weight[i_c]
                output[i_h, i_w, i_c] = np.sum(input_slice * kernel_slice)
                output[i_h, i_w, i_c] += bias[i_c]

    cache = dict()
    cache['Z'] = output
    cache['W'] = weight
    cache['b'] = bias
    cache['A_prev'] = input
    return cache


def conv2d_backward(dZ: np.ndarray, cache: Dict[str, np.ndarray], stride: int,
                    padding: int) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
    """2D Convolution Backward Implemented with NumPy

    Args:
        dZ: (np.ndarray): The derivative of the output of conv.
        cache (Dict[str, np.ndarray]): Record output 'Z', weight 'W', bias 'b'
            and input 'A_prev' of forward function.
        stride (int): Stride for convolution.
        padding (int): The count of zeros to pad on both sides.

    Outputs:
        Tuple[np.ndarray, np.ndarray, np.ndarray]: The derivative of W, b,
            A_prev.
    """
    W = cache['W']
    b = cache['b']
    A_prev = cache['A_prev']
    dW = np.zeros(W.shape)
    db = np.zeros(b.shape)
    dA_prev = np.zeros(A_prev.shape)

    _, _, c_i = A_prev.shape
    c_o, f, f_2, c_k = W.shape
    h_o, w_o, c_o_2 = dZ.shape

    assert (f == f_2)
    assert (c_i == c_k)
    assert (c_o == c_o_2)

    A_prev_pad = np.pad(A_prev, [(padding, padding), (padding, padding),
                                 (0, 0)])
    dA_prev_pad = np.pad(dA_prev, [(padding, padding), (padding, padding),
                                   (0, 0)])

    for i_h in range(h_o):
        for i_w in range(w_o):
            for i_c in range(c_o):
                h_lower = i_h * stride
                h_upper = i_h * stride + f
                w_lower = i_w * stride
                w_upper = i_w * stride + f

                input_slice = A_prev_pad[h_lower:h_upper, w_lower:w_upper, :]
                # forward
                # kernel_slice = W[i_c]
                # Z[i_h, i_w, i_c] = np.sum(input_slice * kernel_slice)
                # Z[i_h, i_w, i_c] += b[i_c]

                # backward
                dW[i_c] += input_slice * dZ[i_h, i_w, i_c]
                dA_prev_pad[h_lower:h_upper,
                            w_lower:w_upper, :] += W[i_c] * dZ[i_h, i_w, i_c]
                db[i_c] += dZ[i_h, i_w, i_c]

    if padding > 0:
        dA_prev = dA_prev_pad[padding:-padding, padding:-padding, :]
    else:
        dA_prev = dA_prev_pad
    return dW, db, dA_prev


@pytest.mark.parametrize('c_i, c_o', [(3, 6), (2, 2)])
@pytest.mark.parametrize('kernel_size', [3, 5])
@pytest.mark.parametrize('stride', [1, 2])
@pytest.mark.parametrize('padding', [0, 1])
def test_conv(c_i: int, c_o: int, kernel_size: int, stride: int, padding: str):

    # Preprocess
    input = np.random.randn(20, 20, c_i)
    weight = np.random.randn(c_o, kernel_size, kernel_size, c_i)
    bias = np.random.randn(c_o)

    torch_input = torch.from_numpy(np.transpose(
        input, (2, 0, 1))).unsqueeze(0).requires_grad_()
    torch_weight = torch.from_numpy(np.transpose(
        weight, (0, 3, 1, 2))).requires_grad_()
    torch_bias = torch.from_numpy(bias).requires_grad_()

    # forward
    torch_output_tensor = torch.conv2d(torch_input, torch_weight, torch_bias,
                                       stride, padding)
    torch_output = np.transpose(
        torch_output_tensor.detach().numpy().squeeze(0), (1, 2, 0))

    cache = conv2d_forward(input, weight, bias, stride, padding)
    numpy_output = cache['Z']

    assert np.allclose(torch_output, numpy_output)

    # backward
    torch_sum = torch.sum(torch_output_tensor)
    torch_sum.backward()
    torch_dW = np.transpose(torch_weight.grad.numpy(), (0, 2, 3, 1))
    torch_db = torch_bias.grad.numpy()
    torch_dA_prev = np.transpose(torch_input.grad.numpy().squeeze(0),
                                 (1, 2, 0))

    dZ = np.ones(numpy_output.shape)
    dW, db, dA_prev = conv2d_backward(dZ, cache, stride, padding)

    assert np.allclose(dW, torch_dW)
    assert np.allclose(db, torch_db)
    assert np.allclose(dA_prev, torch_dA_prev)

池化反向传播：

import numpy as np
from module import Layers 

class Pooling(Layers):
    """

    """
    def __init__(self, name, ksize, stride, type):
        super(Pooling).__init__(name)
        self.type = type
        self.ksize = ksize
        self.stride = stride 

    def forward(self, x):
        b, c, h, w = x.shape
        out = np.zeros([b, c, h//self.stride, w//self.stride]) 
        self.index = np.zeros_like(x)
        for b in range(b):
            for d in range(c):
                for i in range(h//self.stride):
                    for j in range(w//self.stride):
                        _x = i *self.stride
                        _y = j *self.stride
                        if self.type =="max":
                            out[b, d, i, j] = np.max(x[b, d, _x:_x+self.ksize, _y:_y+self.ksize])
                            index = np.argmax(x[b, d, _x:_x+self.ksize, _y:_y+self.ksize])
                            self.index[b, d, _x +index//self.ksize, _y +index%self.ksize ] = 1
                        elif self.type == "aveg":
                            out[b, d, i, j] = np.mean((x[b, d, _x:_x+self.ksize, _y:_y+self.ksize]))
        return out 

    def backward(self, grad_out):
        if self.type =="max":
            return np.repeat(np.repeat(grad_out, self.stride, axis=2),self.stride, axis=3)* self.index 
        elif self.type =="aveg":
            return np.repeat(np.repeat(grad_out, self.stride, axis=2), self.stride, axis=3)/(self.ksize * self.ksize)

我们用pytest进行函数测试：

其中有用例16个pass，说明函数无误。

---

总结

此次实验，通过手动推导并反复理解反向传播的公式和含义，对于CNN的反向传播理解加深，同时也推导了宽卷积的交换性，同时对于11的卷积核理解加深，看来确实~确实11的卷积核有更多的用途，所以才会被辣么多人用，我们也设计了一个简单的CNN模型，实现了卷积层和池化层的反向传播的Numpy版本和Torch版本，对于两种层的反向传播理解更加深入，在搜资料的过程中，我偶然看到一句话就是transformer打败了卷积神经网络，我现在很好奇transformer是怎样更牛的思想，总结就到这里，下边是参考文献：

References:

卷积神经网络(CNN)反向传播算法 - 刘建平Pinard - 博客园 (cnblogs.com)
卷积神经网络(CNN)反向传播算法推导
深度学习入坑篇-池化及numpy实现
CNN的反向传播 - 知乎 (zhihu.com)
卷积神经网络CNN 中用1*1 卷积过滤器的作用及优势
卷积层和池化层的反向传播的实现
算子反向传播的实现思路（以 NumPy 版卷积为例）