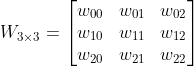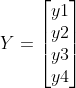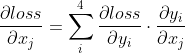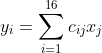神经网络与深度学习 作业7：第五章课后题（1×1 卷积核 | CNN BP）

目录

 习题5-2 证明宽卷积具有交换性，即公式(5.13)。

习题5-3 分析卷积神经网络中用1x1的卷积核的作用。

习题5-4 对于一个输入为100x100x256的特征映射组，使用3x3的卷积核，输出为100x100x256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1x1卷积核，先得到100x100x64的特征映射，再进行3x3的卷积，得到100x100x256的特征映射组，求其时间和空间复杂度。

习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播(公式(5.39))是一种转置关系。

【选做】推导CNN反向传播算法。 

【选做】设计简易CNN模型，分别用Numpy、Python实现卷积层和池化层的反向传播算子，并代入数值测试。

 参考资料

---

 习题5-2 证明宽卷积具有交换性，即公式(5.13)。

证明： 

习题5-3 分析卷积神经网络中用1x1的卷积核的作用。

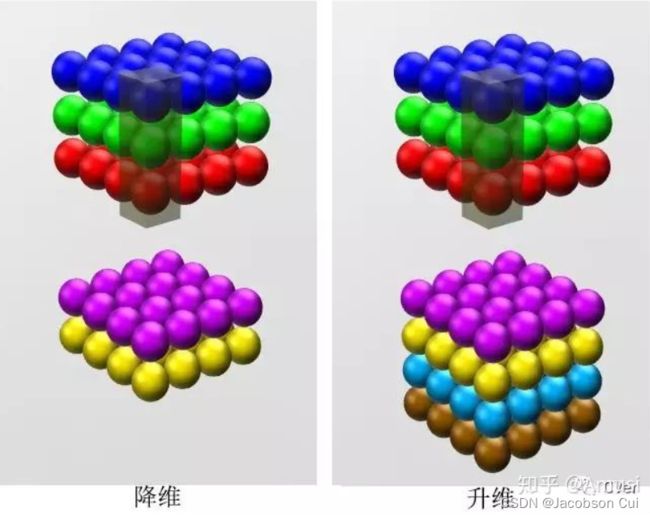
（一）每个1×1的卷积核都试图提取基于相同像素位置的特征的融合表达。可以实现特征升维或降维的目的；

由于 1×1并不会改变 height 和 width，改变通道的第一个最直观的结果，就是可以将原本的数据量进行增加或者减少。这里看其他文章或者博客中都称之为升维、降维。但我觉得维度并没有改变，改变的只是 height × width × channels 中的 channels 这一个维度的大小而已。

（二）1×1的卷积核可以在保持特征图不变的情况下大幅增加非线性特性；

 1*1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep。

（三）将位于每个点位上的所有通道特征进行卷积，实现跨通道信息交互；

 例子：使用1x1卷积核，实现降维和升维的操作其实就是通道间信息的线性组合变化，3x3，64通道的卷积核后面添加一个1x1，28通道的卷积核，就变成了3x3，28通道的卷积核，原来的64个通道就可以理解为跨通道线性组合变成了28通道，这就是通道间的信息交互。

（四）减小计算量，降低时间复杂度。

以GoogLeNet的3a模块为例，输入的feature map是28×28×192，3a模块中1×1卷积通道为64，3×3卷积通道为128,5×5卷积通道为32，如果是左图结构，那么卷积核参数为1×1×192×64+3×3×192×128+5×5×192×32，而右图对3×3和5×5卷积层前分别加入了通道数为96和16的1×1卷积层，这样卷积核参数就变成了1×1×192×64+（1×1×192×96+3×3×96×128）+（1×1×192×16+5×5×16×32），参数大约减少到原来的三分之一。

习题5-4 对于一个输入为100x100x256的特征映射组，使用3x3的卷积核，输出为100x100x256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1x1卷积核，先得到100x100x64的特征映射，再进行3x3的卷积，得到100x100x256的特征映射组，求其时间和空间复杂度。

情况一：=100;=3;=256 ;=256

时间复杂度一：100×100×3×3×256×256 = 5898240000

空间复杂度一：100×100×256 = 2560000

---

情况二：=100;=1;=3;=256;=64;=64;=256

时间复杂度二：100×100×1×1×256×64 + 100×100×3×3×64×256 = 1638400000

空间复杂度二：100×100×64 + 100×100×256 = 3200000

习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播(公式(5.39))是一种转置关系。

以一个3×3的卷积核为例，输入为X输出为Y

                             

将4×4的输入特征展开为16×1的矩阵，y展开为4×1的矩阵，将卷积计算转化为矩阵相乘 

                  

因为： ；且即

所以:

对比正向： ,所以两者是一种转置关系。

【选做】推导CNN反向传播算法。 

1、已知池化层的误差，反向推导上一隐藏层的误差 

在前向传播时，池化层我们会用MAX或者Average对输入进行池化，池化的区域大小已知。现在我们反过来，要从缩小后区域的误差，还原前一层较大区域的误差。这个过程叫做upsample。假设我们的池化区域大小是2x2。第l层误差的第k个子矩阵为: 

如果池化区域表示为a*a大小，那么我们把上述矩阵上下左右各扩展a-1行和列进行还原：

如果是MAX，假设我们之前在前向传播时记录的最大值位置分别是左上，右下，右上，左下，则转换后的矩阵为：

如果是Average，则进行平均，转换后的矩阵为：

上边这个矩阵就是误差矩阵经过upsample之后的矩阵，那么，由后一层误差推导出前一层误差的公式为：

上式和普通网络的反向推导误差很类似：

可以看到，只有第一项不同。

2、已知卷积层的误差，反向推导上一隐藏层的误差

公式如下：

普通网络的反向推导误差的公式：

可以看到区别在于，下一层的权重w的转置操作，变成了旋转180度的操作，也就是上下翻转一次，左右再翻转一次，这其实就是“卷积”一词的意义（我们可简单理解为数学上的trick），可参考下图，Q是下一层的误差，周围补0方便计算，W是180度翻转后的卷积核，P是W和Q做卷积的结果：

3、已知卷积层的误差，推导该层的W,b的梯度

经过以上各步骤，我们已经算出每一层的误差了，那么：

1. 对于全连接层，可以按照普通网络的反向传播算法求该层W,b的梯度。
2. 对于池化层，它并没有W,b,也不用求W,b的梯度。
3. 只有卷积层的W,b需要求出，先看w：

   

   再对比一下普通网络的求w梯度的公式，发现区别在于，对前一层的输出做翻转180度的操作：

   

   而对于b,则稍微有些特殊，因为在CNN中，误差δ是三维张量，而b只是一个向量，不能像普通网络中那样直接和误差δ相等。通常的做法是将误差δ的各个子矩阵的项分别求和，得到一个误差向量，即为b的梯度：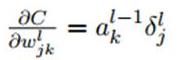

   

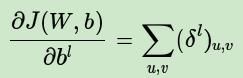
【选做】设计简易CNN模型，分别用Numpy、Python实现卷积层和池化层的反向传播算子，并代入数值测试。

卷积层的反向传播

import numpy as np
import torch.nn as nn


class Conv2D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride, padding):
        super(Conv2D, self).__init__()

        self.in_channels = in_channels
        self.out_channels = out_channels
        self.ksize = kernel_size
        self.stride = stride
        self.padding = padding

        self.weights = np.random.standard_normal((out_channels, in_channels, kernel_size, kernel_size))
        self.bias = np.zeros(out_channels)

        self.grad_w = np.zeros(self.weights.shape)
        self.grad_b = np.zeros(self.bias.shape)

    def forward(self, x):
        self.x = x
        weights = self.weights.reshape(self.out_channels, -1)  # o,ckk

        x = np.pad(x, ((0, 0), (0, 0), (self.padding, self.padding), (self.padding, self.padding)), 'constant',
                   constant_values=0)
        b, c, h, w = x.shape

        self.out = np.zeros(
            (b, self.out_channels, (h - self.ksize) // self.stride + 1, (w - self.ksize) // self.stride + 1))

        self.col_img = self.im2col(x, self.ksize, self.stride)  # bhw * ckk
        out = np.dot(weights, self.col_img.T).reshape(self.out_channels, b, -1).transpose(1, 0, 2)

        self.out = np.reshape(out, self.out.shape)

        return self.out

    def backward(self, grad_out):
        b, c, h, w = self.out.shape  #

        grad_out_ = grad_out.transpose(1, 0, 2, 3)  # b,oc,h,w * (bhw , ckk)
        grad_out_flat = np.reshape(grad_out_, [self.out_channels, -1])

        self.grad_w = np.dot(grad_out_flat, self.col_img).reshape(self.grad_w.shape)
        self.grad_b = np.sum(grad_out_flat, axis=1)
        tmp = self.ksize - self.padding - 1
        grad_out_pad = np.pad(grad_out, ((0, 0), (0, 0), (tmp, tmp), (tmp, tmp)), 'constant', constant_values=0)

        flip_weights = np.flip(self.weights, (2, 3))
        # flip_weights = np.flipud(np.fliplr(self.weights)) # rot(180)
        flip_weights = flip_weights.swapaxes(0, 1)  # in oc
        col_flip_weights = flip_weights.reshape([self.in_channels, -1])

        weights = self.weights.transpose(1, 0, 2, 3).reshape(self.in_channels, -1)

        col_grad = self.im2col(grad_out_pad, self.ksize, 1)  # bhw,ckk

        # (in,ckk) * (bhw,ckk).T
        next_eta = np.dot(weights, col_grad.T).reshape(self.in_channels, b, -1).transpose(1, 0, 2)

        next_eta = np.reshape(next_eta, self.x.shape)

        return next_eta

    def zero_grad(self):
        self.grad_w = np.zeros_like(self.grad_w)
        self.grad_b = np.zeros_like(self.grad_b)

    def update(self, lr=1e-3):
        self.weights -= lr * self.grad_w
        self.bias -= lr * self.grad_b

    def im2col(self, x, k_size, stride):
        b, c, h, w = x.shape
        image_col = []
        for n in range(b):
            for i in range(0, h - k_size + 1, stride):
                for j in range(0, w - k_size + 1, stride):
                    col = x[n, :, i:i + k_size, j:j + k_size].reshape(-1)
                    image_col.append(col)

        return np.array(image_col)


class Layers():
    def __init__(self, name):
        self.name = name

    # 前向
    def forward(self, x):
        pass

    # 梯度置零
    def zero_grad(self):
        pass

    # 后向
    def backward(self, grad_out):
        pass

    # 参数更新
    def update(self, lr=1e-3):
        pass


class Module():
    def __init__(self):
        self.layers = []  # 所有的Layer

    def forward(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

    def backward(self, grad):
        for layer in reversed(self.layers):
            layer.zero_grad()
            grad = layer.backward(grad)

    def step(self, lr=1e-3):
        for layer in reversed(self.layers):
            layer.update(lr)


# test_conv
if __name__ == '__main__':
    x = np.array([[[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]]])
    conv = Conv2D(2, 3, 2, 1, 0)
    y = conv.forward(x)
    print(y.shape)
    loss = y - (y + 1)
    grad = conv.backward(loss)
    print(grad.shape)

池化层的反向传播

import numpy as np
import torch.nn as nn


class MaxPooling(nn.Module):
    def __init__(self, ksize=2, stride=2):
        super(MaxPooling,self).__init__()
        self.ksize = ksize
        self.stride = stride 

    def forward(self, x):
        n,c,h,w = x.shape
        out = np.zeros([n, c, h//self.stride,w//self.stride])
        self.index = np.zeros_like(x)
        for b in range(n):
            for d in range(c):
                for i in range(h//self.stride):
                    for j in range(w//self.stride):
                        _x = i*self.stride
                        _y = j*self.stride
                        out[b, d ,i , j] = np.max(
                            x[b, d ,_x:_x+self.ksize, _y:_y+self.ksize])
                        index = np.argmax(x[b, d ,_x:_x+self.ksize, _y:_y+self.ksize])
                        self.index[b,d,_x+index//self.ksize, _y+index%self.ksize] = 1
        return out

    def backward(self, grad_out):
        return np.repeat(np.repeat(grad_out, self.stride, axis=2), self.stride, axis=3) * self.index

 

 参考资料

干货 | 深度学习之CNN反向传播算法详解 - 腾讯云开发者社区-腾讯云 (tencent.com)

邱锡鹏《神经网络与深度学习》—— 部分习题答案整理_小笠凹的博客-CSDN博客

卷积神经网络中的1x1卷积核的作用_幸运六叶草的博客-CSDN博客

用numpy实现CNN卷积神经网络 - qxcheng - 博客园 (cnblogs.com)