5.2 imnoise函数
imnoise2函数
function R = imnoise2(type, M, N, a, b)
%type 噪声类型 M,N噪声矩阵大小M x N a表示均值,b表示标准差
%IMNOISE2 Generates an array of random numbers with specified PDF.
% R = IMNOISE2(TYPE, M, N, A, B) generates an array, R, of size
% M-by-N, whose elements are random numbers of the specified TYPE
% with parameters A and B. If only TYPE is included in the
% input argument list, a single random number of the specified
% TYPE and default parameters shown below is generated. If only
% TYPE, M, and N are provided, the default parameters shown below
% are used. If M = N = 1, IMNOISE2 generates a single random
% number of the specified TYPE and parameters A and B.
%
% Valid values for TYPE and parameters A and B are:
%
% 'uniform' Uniform random numbers in the interval (A, B).
% The default values are (0, 1).
% 'gaussian' Gaussian random numbers with mean A and standard
% deviation B. The default values are A = 0, B = 1.
% 'salt & pepper' Salt and pepper numbers of amplitude 0 with
% probability Pa = A, and amplitude 1 with
% probability Pb = B. The default values are Pa =
% Pb = A = B = 0.05. Note that the noise has
% values 0 (with probability Pa = A) and 1 (with
% probability Pb = B), so scaling is necessary if
% values other than 0 and 1 are required. The noise
% matrix R is assigned three values. If R(x, y) =
% 0, the noise at (x, y) is pepper (black). If
% R(x, y) = 1, the noise at (x, y) is salt
% (white). If R(x, y) = 0.5, there is no noise
% assigned to coordinates (x, y).
% 'lognormal' Lognormal numbers with offset A and shape
% parameter B. The defaults are A = 1 and B =
% 0.25.
% 'rayleigh' Rayleigh noise with parameters A and B. The
% default values are A = 0 and B = 1.
% 'exponential' Exponential random numbers with parameter A. The
% default is A = 1.
% 'erlang' Erlang (gamma) random numbers with parameters A
% and B. B must be a positive integer. The
% defaults are A = 2 and B = 5. Erlang random
% numbers are approximated as the sum of B
% exponential random numbers.
% Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
% Digital Image Processing Using MATLAB, Prentice-Hall, 2004
% $Revision: 1.5 $ $Date: 2003/10/12 23:37:29 $
% Set default values.
%若参数个数为1,则给a,b,M,N赋值
if nargin == 1
a = 0; b = 1;
M = 1; N = 1;
elseif nargin == 3
a = 0; b = 1;
end
% Begin processing. Use lower(type) to protect against input being
% capitalized.
switch lower(type)
case 'uniform'
R = a + (b - a)*rand(M, N);
case 'gaussian'
R = a + b*randn(M, N);
case 'salt & pepper'
if nargin <= 3
a = 0.05; b = 0.05;
end
% Check to make sure that Pa + Pb is not > 1.
if (a + b) > 1
error('The sum Pa + Pb must not exceed 1.')
end
R(1:M, 1:N) = 0.5;
% Generate an M-by-N array of uniformly-distributed random numbers
% in the range (0, 1). Then, Pa*(M*N) of them will have values <=
% a. The coordinates of these points we call 0 (pepper
% noise). Similarly, Pb*(M*N) points will have values in the range
% > a & <= (a + b). These we call 1 (salt noise).
X = rand(M, N);
c = find(X <= a);
R(c) = 0;
u = a + b;
c = find(X > a & X <= u);
R(c) = 1;
case 'lognormal'
if nargin <= 3
a = 1; b = 0.25;
end
R = a*exp(b*randn(M, N));
case 'rayleigh'
R = a + (-b*log(1 - rand(M, N))).^0.5;
case 'exponential'
if nargin <= 3
a = 1;
end
if a <= 0
error('Parameter a must be positive for exponential type.')
end
k = -1/a;
R = k*log(1 - rand(M, N));
case 'erlang'
if nargin <= 3
a = 2; b = 5;
end
if (b ~= round(b) | b <= 0)
error('Param b must be a positive integer for Erlang.')
end
k = -1/a;
R = zeros(M, N);
for j = 1:b
R = R + k*log(1 - rand(M, N));
end
otherwise
error('Unknown distribution type.')
end
书中画出各噪声的直方图
>> %以下显示所有类型的直方图,没有赋值的取默认值
R=imnoise2('gaussian',100000,1,0,1);
subplot(3,2,1),hist(R,50),title('高斯')%用hist显示直方图
R=imnoise2('salt & pepper',100000,10);
subplot(3,2,2),hist(R,50),title('焦盐')
R=imnoise2('lognormal',100000,10);
subplot(3,2,3),hist(R,50),title('对数正态')
R=imnoise2('rayleigh',100000,1);
subplot(3,2,4),hist(R,50),title('瑞利')
R=imnoise2('exponential',100000,1);
subplot(3,2,5),hist(R,50),title('指数')
R=imnoise2('erlang',100000,1);
subplot(3,2,6),hist(R,50),title('厄兰')
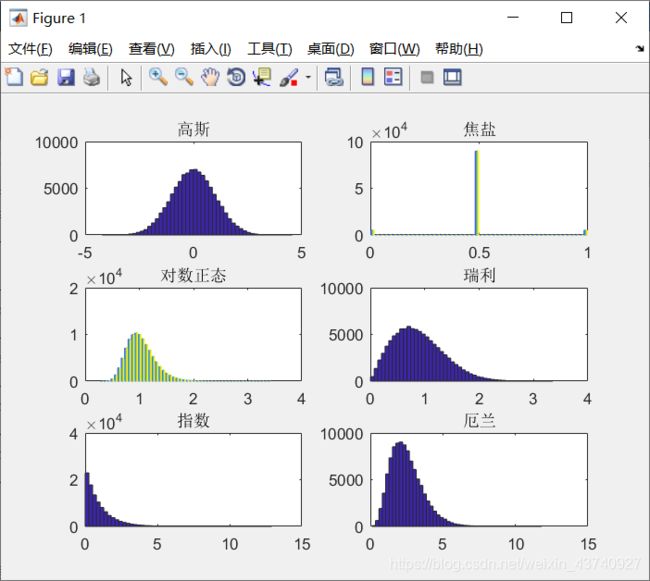

imnoise2用来产生噪声模型,上式gaussian代表噪声服从高斯分布,100000,1代表产生的噪声矩阵为100000*1大小,0代表高斯分布随机数的均值,1代表高斯分布随机数的标准偏差。
imnoise3
function [r, R, S] = imnoise3(M, N, C, A, B)
% IMNOISE3 Generates periodic noise.
% [r, R, S] = IMNOISE3(M, N, C, A, B), generates a spatial sinusoidal
% noise pattern, r, of size M-by-N, its Fourier transform, R, and
% spectrum, S. The remaining parameters are as follows:
% C is a K-by-2 matrix containing K pairs of frequency domain coordinates
% (u, v) indicating the locations of impulses in the frequency domain.
% These locations are with respect to the frequency rectangele center at
% (M/2 + 1, N/2 + 1). Only one paor of coordinates is required for each
% impulse. The program automatically generates the locations of the
% conjugate symmetric impulses. These impulse paird determine the
% frequency content of r.
% A is a 1-by-k vector that contains the ampitude of each of the K
% impulse pairs. If A is not included in the argument, the default used
% is A = ONES(1, K). B is then automatically set to its default values
% (see next paragraph). The value specified for A(j) is associated with
% the coordinates in C(j, 1:2).
% B is a K-by-2 matrix containing the Bx and By phase components for each
% impulse pair. The default values for B are B(1:K, 1:2) = 0.
% Chinese : 根据5.2.3周期噪声的DFT公式得到,A是振幅,u0,v0是关于x轴和y轴确定正弦频率,这里是C表示
% Bx和By是关于原点的相移。
% [r,R,S] = IMNOISE3(M,N,C,A,B),产生大小为M-by-N的空间正弦噪声模式r,
% 其傅里叶变换R和频谱S。 其余参数如下:
% C是K-by-2矩阵,包含K对频域坐标(u,v), 表示频域中脉冲的位置。
% 这些位置相对于频率矩形中心(M / 2 + 1,N / 2 + 1)。 每个脉冲只需要一个坐标。
% 程序自动生成共轭对称脉冲的位置。 这些脉冲信号决定了r的频率成分。
% A是1×k矢量,包含每个K脉冲对的幅度。 如果参数中不包含A,则使用的默认值为A = ONES(1,K)。
% 然后B自动设置为其默认值(参见下一段)。 为A(j)指定的值与C(j,1:2)中的坐标相关联。
% B是K-by-2矩阵,包含每个脉冲对的Bx和By相位分量。 B的默认值为B(1:K,1:2)= 0。
% Process input parameters.
[K, n] = size(C);
if nargin ==3
A(1:K) = 1.0;
B(1:K, 1:2) = 0;
elseif nargin == 4
B(1:K, 1:2) = 0;
end
% Generate R
R = zeros(M, N);
for j = 1:K
u1 = M/2 + 1 + C(j, 1);
v1 = N/2 + 1 + C(j, 2);
R(u1, v1) = i * (A(j)/2) * exp(i * 2 * pi * C(j, 1)* B(j,1)/M); % 位于(u + u0, v + v0) 的冲击处的R
% Complex conjugate.
u2 = M/2 + 1 - C(j, 1);
v2 = N/2 + 1 - C(j, 2);
R(u2, v2) = -i * (A(j)/2) * exp(i * 2 * pi * C(j, 2)* B(j,2)/M);% 位于(u - u0, v - v0) 的冲击处的R
end
% Compute spectrum and spatial sinusoidal pattern.
S = abs(R);
r = real(ifft2(ifftshift(R)));