以Cart Pole为环境,实现DQN和PG算法
一、 实验题目
以Cart Pole为环境,实现DQN和PG算法
二、 实验内容
1.算法原理
强化学习—DQN算法原理详解binbigdata的博客-CSDN博客dqn算法
DeepRL系列(7): DQN(Deep Q-learning)算法原理与实现 - 知乎 (zhihu.com)
DQN:
DQN算法是一种将Q_learning通过神经网络近似值函数的一种方法,强化学习是一个反复迭代的过程,每一次迭代要解决两个问题:给定一个策略求值函数,和根据值函数来更新策略。
上面说过DQN使用神经网络来近似值函数,即神经网络的输入是state ss,输出是Q(s,a),∀a∈AQ(s,a),∀a∈A (action space)。通过神经网络计算出值函数后,DQN使用ϵ−greedyϵ−greedy策略来输出action(第四部分中介绍)。值函数网络与ϵ−greedyϵ−greedy策略之间的联系是这样的:首先环境会给出一个obs,智能体根据值函数网络得到关于这个obs的所有Q(s,a)Q(s,a),然后利用ϵ−greedyϵ−greedy选择action并做出决策,环境接收到此action后会给出一个奖励Rew及下一个obs。这是一个step。此时我们根据Rew去更新值函数网络的参数。接着进入下一个step。如此循环下去,直到我们训练出了一个好的值函数网络。
大致流程是首先初始化值函数矩阵,开始episode,然后选择一个状态state,同时智能体根据自身贪婪策略,选择action, 经过智能体将动作运用后得到一个奖励和计算值函数,继续迭代下一个流程。
DIMA-PG算法原理 - 知乎 (zhihu.com)
PG:
优化的过程是一个迭代的形式:
-
对于每一个Agent,优化它对应的θn
-
然后将θn 的变化总结到θ中,促进θ的更新
-
首先,从Agent总集Pop中选取 N 个Agent作为抽样,服从 P(Pop)分布。
-
初始化Central Policy——πθ
-
对于第n个Agent,将其Policy参数 θN初始化为Central Policy 参数 当前的值 ,Agent n依据该Policy进行动作并收集trajectory 。此时其他所有Agent的Policy参数也等于Central Policy参数 。
-
根据下面公式对Agent n的Policy参数进行优化更新: θ <- θ + α*∇θ*logπθ(St,At)*Vt 。该过程并不是只能一步就更新,可以分为k步逐步更新。
-
Agent n的Policy参数更新为 θn之后,假设其他Agent仍然采取Central Policy ,再进行动作并收集trajectory 。
-
根据收集到数据 ,计算目标函数的优化梯度。
-
对于总共N个Agent所获得的目标函数梯度进行汇总,然后用以下公式对Central Policy参数 进行参数更新:
-
再回到第1步,进行迭代。
2.伪代码
DQN:
- 首先初始化Memory D,它的容量为N;
- 初始化Q网络,随机生成权重ωω;
- 初始化target Q网络,权重为ω−=ωω−=ω;
- 循环遍历episode =1, 2, …, M:
- 初始化initial state S1S1;
- 循环遍历step =1,2,…, T:
- 用ϵ−greedyϵ−greedy策略生成action atat:以ϵϵ概率选择一个随机的action,或选择at=maxaQ(St,a;ω)at=maxaQ(St,a;ω);
- 执行action atat,接收reward rtrt及新的state St+1St+1;
- 将transition样本 (St,at,rt,St+1)(St,at,rt,St+1)存入D中;
- 从D中随机抽取一个minibatch的transitions (Sj,aj,rj,Sj+1)(Sj,aj,rj,Sj+1);
- 令yj=rjyj=rj,如果 j+1j+1步是terminal的话,否则,令 yj=rj+γmaxa′Q(St+1,a′;ω−)yj=rj+γmaxa′Q(St+1,a′;ω−);
- 对(yj−Q(St,aj;ω))2(yj−Q(St,aj;ω))2关于ωω使用梯度下降法进行更新;
- 每隔C steps更新target Q网络,ω−=ωω−=ω。PG:
function PG
initialise θ arbitrary
for each episode {S1,A1,R2,……,St-1,At-1,Rt} ~ πθ
for t = 1 to T-1
θ <- θ + α*∇θ*logπθ(St,At)*Vt
end for
end for
return θ
end function3.关键代码展示(带注释)
首先了解一下CartPole环境,参考如下:
OpenAI Gym 经典控制环境介绍——CartPole(倒立摆)思绪无限的博客-CSDN博客cartpole
gym学习及二次开发小草cys的博客-CSDN博客env.reset()
gym的核心接口是Env。作为统一的环境接口,Env包含下面几个核心方法:
reset(self):重置环境的状态,返回观察。 step(self, action):推进一个时间步长,返回observation, reward, done, info。 render(self, mode=‘human’, close=False):重绘环境的一帧。默认模式一般比较友好,如弹出一个窗口。 close(self):关闭环境,并清除内存。
观测 (Observations):
在上面代码中使用了env.step()函数来对每一步进行仿真,在Gym中,env.step()会返回 4 个参数:
-
观测 Observation (Object):当前step执行后,环境的观测(类型为对象)。
-
奖励 Reward (Float): 执行上一步动作(action)后,智能体( agent)获得的奖励(浮点类型),不同的环境中奖励值变化范围也不相同,但是强化学习的目标就是使得总奖励值最大;
-
完成 Done (Boolen): 表示是否需要将环境重置 env.reset。大多数情况下,当 Done 为True 时,就表明当前回合(episode)或者试验(tial)结束。
-
信息 Info (Dict): 针对调试过程的诊断信息。在标准的智体仿真评估当中不会使用到这个info。
游戏奖励 (reward):在gym的Cart Pole环境(env)里面,左移或者右移小车的action之后,env会返回一个+1的reward。其中CartPole-v0中到达200个reward之后,游戏也会结束,而CartPole-v1中则为500。本次实验使用CartPole-v0环境。
DQN部分重要代码
整体学习参考部分:
基于DQN算法解决Cart-Pole问题_高小喵的博客-CSDN博客
【动手学强化学习(1)DQN】CarPole DQN的实现 - 知乎 (zhihu.com)
首先导入需要的库函数
import gym
import numpy as np
import torch
import time
import matplotlib.pyplot as plt
from collections import deque
import random设置超参数
如何调整DQN中的超参数
(1条消息) DQN调整超参数体会万德1010的博客-CSDN博客dqn调参
# ---------- 超参数 ---------- #
BATCH_SIZE = 64 # 样本数量
gamma = 0.95 # reward discount
LEARNING_RATE = 0.001 # 学习率
TARGET_UPDATE = 10 # 目标网络更新频率
hidden_dim = 16
EPSILON = 0.9 # greedy policyQNetwork
class QNetwork(nn.Module): # 三层神经网络
# 继承nn.Module类,并重新实现构造函数__init__构造函数和forward这两个方法
def __init__(self, input_dim, output_dim, hidden_dim):
super(QNetwork, self).__init__() # # 继承__init__功能
self.layer1 = nn.Sequential(nn.Linear(input_dim, hidden_dim),nn.PReLU())
self.layer2 = nn.Sequential(nn.Linear(hidden_dim, hidden_dim),nn.PReLU())
self.layer3 = nn.Sequential(nn.Linear(hidden_dim, hidden_dim),nn.PReLU())
self.final = nn.Linear(hidden_dim, output_dim)
def forward(self, x: torch.Tensor): # call方法自动调用 forward 函数
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.final(x)
return xpytorch教程之nn.Module类详解——使用Module类来自定义模型LoveMIss-Y的博客-CSDN博客pytorch 自定义module
torch.nn是专门为神经网络设计的模块化接口。nn构建于Autograd之上,可以用来定义和运行神经网络。nn.Module是nn中十分重要的类,包含网络各层的定义及forward方法。
我们在定义自已的网络的时候,需要继承nn.Module类,并重新实现构造函数init构造函数和forward这两个方法。但有一些注意技巧:
(1)一般把网络中具有可学习参数的层(如全连接层、卷积层等)放在构造函数init()中。
(2)一般把不具有可学习参数的层(如ReLU、dropout、BatchNormanation层)可放在构造函数中,也可不放在构造函数中,如果不放在构造函数init里面,则在forward方法里面可以使用nn.functional来代替
(3)forward方法是必须要重写的,它是实现模型的功能,实现各个层之间的连接关系的核心。只要在 nn.Module的子类中定义了forward函数,backward函数就会被自动实现(利用Autograd)。
Module类是非常灵活的,可以有很多灵活的实现方式,本次实验采取Sequential来包装层,即将几个层包装在一起作为一个大的层(块)。
ReplayMemory
class ReplayMemory():
def __init__(self, capacity): # 存储容量
self.capacity = capacity
self.memory = [] # 保存 batch 的列表
def push(self, experience):
self.memory.append(experience) # 把经验数据存储起来
if len(self.memory) > self.capacity: # 如果存储数据超过了容量,删除以前经验数据
del self.memory[0]
def sample(self, batch_size): # 对历史数据随机采样, batch_size = 64
return random.sample(self.memory, batch_size)
def length(self):
return len(self.memory)这个部分是存储记忆部分的,push用于将传入的数据保存,sample 随机返回 batch_size 的数据。
Agent
class Agent(object):
def __init__(self, n_states, n_actions, hidden_dim):
self.q_evaluate = QNetwork(n_states, n_actions, hidden_dim) # 评估网络,用来进行计算价值
self.q_target = QNetwork(n_states, n_actions, hidden_dim) # 目标网络
self.mse_loss = torch.nn.MSELoss() # 损失函数MSE
self.optim = optim.Adam(self.q_evaluate.parameters(), lr = LEARNING_RATE)
# 用到评估网络q_evaluate.parameters传入优化器,对网络参数进行优化
self.n_states = n_states # 4
self.n_actions = n_actions # 2
self.replay_memory = ReplayMemory(10000) # 定义存储容量
def get_action(self, state, eps): # state是二阶状态张量
if np.random.uniform() < eps: # 生成一个在[0,1)内的随机数,如果小于 EPSILON,选择最优动作
return self.q_evaluate(state).data.max(1)[1].view(1, 1)
# .max(1)[1]选择输出结果中最大值对应的动作,.view(1, 1)转成一阶张量
else:
return torch.tensor([[np.random.randint(self.n_actions)]]) # 返回动作动作区间里面的随机的一个动作
def learn(self, experiences, gamma):
transitions = self.replay_memory.sample(BATCH_SIZE) # 随机取batch_size个历史数据
states, actions, rewards, next_states, dones = [[] for x in range(5)]
for i in range(len(transitions)): # 将参数拆开存放并进行拼接
states.append(transitions[i][0].tolist()[0])
actions.append(transitions[i][1].tolist()[0])
rewards.append(transitions[i][2].tolist()[0])
next_states.append(transitions[i][3].tolist()[0])
dones.append(transitions[i][4].tolist()[0])
states = torch.Tensor(states) # 转换成tensor类型数据
actions = torch.LongTensor(actions) # 浮点转换为64位整型数据
rewards = torch.Tensor(rewards)
next_states = torch.Tensor(next_states)
dones = torch.Tensor(dones)
Q_expected = self.q_evaluate(states).gather(1, actions)
# self.q_evaluate(states)为shape=(xxx, 2)的二维表,动作数为2
# 使用gather()函数即可轻松获取批量状态对应批量动作
Q_targets_next = self.q_target(next_states).detach().max(1)[0] # 下一步的期望
Q_targets = rewards + (gamma * Q_targets_next * (1 - dones)) # 相当于真值
self.optim.zero_grad() # 将梯度初始化为零
loss = self.mse_loss(Q_expected, Q_targets.unsqueeze(1)) # 列方向扩充维度
loss.backward() # 反向传播求梯度
self.optim.step() # 更新所有参数
return lossAgent部分是最重要的,包含了新动作的更新以及学习,首先给出一些参考资料:
pytorch源码阅读系列之Parameter类 - 知乎 (zhihu.com)
PyTorch中的parameters - 知乎 (zhihu.com)
torch.optim优化算法理解之optim.Adam()KGzhang的博客-CSDN博客torch.optim.adam
首先利用上述定义过的QNetwork类来创建评估网络 q_evaluate 以及目标网络 q_target ,self.optim = optim.Adam(self.q_evaluate.parameters(), lr = LEARNING_RATE) 这句代码利用评估网络q_evaluate.parameters传入优化器,对网络参数进行优化。
Parameter作为Module类的参数,可以自动的添加到Module类的参数列表中,并且可以使用Module.parameters()提供的迭代器获取到。在分析Parameter的实现代码之前,首先自定义一个Net,用于验证Net实例属性为Parameter对象时Net会自动将次Parameter对象注册到参数列表中
为了使用torch.optim,需先构造一个优化器对象Optimizer,用来保存当前的状态,并能够根据计算得到的梯度来更新参数。要构建一个优化器optimizer,你必须给它一个可进行迭代优化的包含了所有参数(所有的参数必须是变量s)的列表。 然后,您可以指定程序优化特定的选项,例如学习速率,权重衰减等。
获得下一个动作通过eps与随机数比较,np.random.uniform() < eps则选择最优动作,否则随机返回一个动作
学习过程是这样子的,首先利用 replay_memory.sample(BATCH_SIZE) 随机取batch_size个历史数据,然后对数据进行处理,分别得到关于 states, actions, rewards, next_states, dones 的 tensor 形式数据。再使用gather()函数即可轻松获取批量状态对应批量动作,最后就是强化学习的老套路:将梯度初始化为零,反向传播求梯度,更新所有参数。
gather函数使用:图解PyTorch中的torch.gather函数 - 知乎 (zhihu.com)
强化学习的几个步骤:torch代码解析 为什么要使用optimizer.zero_grad()scut_salmon的博客-CSDN博客zero_grad()
创建了 Agent 类以后,DQN最后一部分就是训练。
def run_episode(env, agent, eps):
state = env.reset() # 环境初始化
FT = torch.FloatTensor
done = False # 初始化游戏结束标志位
total_reward = 0
loss = 0
while not done:
# env.render() # 显示小车
action = agent.get_action(FT([state]), eps) # 根据输入state输出action
# action.item() = 0 小车左移,action.item() = 1,小车右移
next_state, reward, done, info = env.step(action.item()) # env.step() 有四个返回值,分别代表着 反馈,奖励,是否结束,其他信息
total_reward += reward
agent.replay_memory.push((FT([state]),action,FT([reward]),FT([next_state]),FT([done]))) # 保存历史经验
if agent.replay_memory.length() > BATCH_SIZE:
batch = agent.replay_memory.sample(BATCH_SIZE) # 随机抽取batch个历史经验数据
loss = agent.learn(batch, gamma).item() # 更新evaluate网络
state = next_state
return total_reward,lossenv.render() 可以看见小车具体运动情况,为了避免多一个弹窗,在这里我把它注释掉了。
state = env.reset() 是环境初始化,得到四个初始数据,再利用 torch.FloatTensor转成 FloatTensor存储形式,于是我们就可以用之前创建的 Agent 类来获得 action,再通过 action 得到
next_state, reward, done,统计总的 reward,并将本次经验传入 Agent 类的存储表中。再通过随机抽取batch个历史经验数据,更新evaluate网络。DQN的学习过程大概就是这样子,接下来看看PG。
PG部分重要代码
整体学习参考部分:
policy gradient解析
大部分内容与DQN是相似的,这里就简单说一些不同之处。
Net
与DQN类似,首先还是创建一个 Net 类,只是采用了不同的连接策略,如下:
class Net(nn.Module):
# 离散空间采用了 softmax policy 来参数化策略
def __init__(self, n_states, n_actions):
super(Net, self).__init__()
self.fc1 = nn.Linear(n_states, 10) # 设置第一个全连接层(输入层到隐藏层): 状态数个神经元到10个神经元
self.fc2 = nn.Linear(10, n_actions) # 设置第二个全连接层(隐藏层到输出层): 10个神经元到动作数个神经元
self.fc1.weight.data.normal_(0, 0.1) # 权重初始化 (均值为0,方差为0.1的正态分布)
self.fc2.weight.data.normal_(0, 0.1) # 权重初始化 (均值为0,方差为0.1的正态分布)
def forward(self, x):
x = self.fc1(x)
x = F.relu(x)
action_score = self.fc2(x)
return F.softmax(action_score, dim = 1)PolicyGradient
class PolicyGradient(nn.Module):
def __init__(self, n_states, n_actions):
super(PolicyGradient, self).__init__()
self.net = Net(n_states, n_actions)
self.optimizer = optim.Adam(self.net.parameters(), lr = LR)
self.log_list = [] # 记录每个时刻的log p(a|s)
self.reward_list = [] # 一个数组,记录每个时刻做完动作后的reward
def get_action(self, state):
# 选择动作,这个动作不是根据Q值来选择,而是使用softmax生成的概率来选
# 在policy gradient中,不需要epsilon-greedy,因为概率本身就具有随机性
state = torch.from_numpy(state).float().unsqueeze(0)
possibility = self.net(state) # 在状态state下各个action被执行的概率
m = Categorical(possibility) # 生成分布
action = m.sample() # 从分布中采样(根据各个action的概率)
self.log_list.append(m.log_prob(action)) # 即 logP(a_t|s_t,θ)
return action.item() # 返回一个action
def store_transition(self, reward):
self.reward_list.append(reward)
def learn(self):
R = 0
policy_loss = []
returns = []
self.reward_list.reverse()
for r in self.reward_list: # 衰减的奖励和
R = r + gamma * R
returns.insert(0, R) # 将R插入到指定的位置0处(折扣奖励)
returns = torch.tensor(returns)
returns = (returns - returns.mean()) / (returns.std() + eps) # 归一化
for log_prob, R in zip(self.log_list, returns):
policy_loss.append(-log_prob * R) # 折扣奖励*logP(a|s)
self.optimizer.zero_grad() # 将梯度初始化为零
policy_loss = torch.cat(policy_loss).sum() # loss_sum
policy_loss.backward() # 反向传播求梯度
self.optimizer.step() # 更新所有参数
self.log_list.clear()
self.reward_list.clear()
return policy_loss相比于前面的 DQN 算法,PG 算法同样需要有函数 get_action 去获取动作,但与之不同的是选择动作,DQN使用 epsilon-greedy 策略选择,而PG 算法的这个动作不是根据Q值来选择,而是使用softmax生成的概率来选,在policy gradient中,不需要 epsilon-greedy,因为概率本身就具有随机性。
DQN有专门的存储类,但是PG没有开,相比于前面的 DQN 算法,PG 算法使用了更多的序列,这是因为 PG 算法是一个在线策略算法,之前收集到的轨迹数据不会被再次利用。仅是使用 store_transition 存储 reward 。
def train():
reward_deque = deque(maxlen = 100) # 连续出现10个200,即训练成功 #双向队列
time_start = time.time()
for i in range(2000):
state = env.reset() # 环境初始化
sum_reward = 0
while (True):
# env.render() # 是否显示小车
action = PG.get_action(state)
state, reward, done, info = env.step(action)
sum_reward += reward
PG.store_transition(reward)
if (done):
break
PG.learn()
env.close()总的来说,PG算法根据当前policy参数采样得到N个Trajectory,计算一次期望reward,然后梯度上升的方法更新policy参数,用更新后的policy再进行下一轮采样,如此往复直到收敛,得到期望reward最大的policy。
三、实验结果及分析
实验结果展示示例(可图可表可文字,尽量可视化)
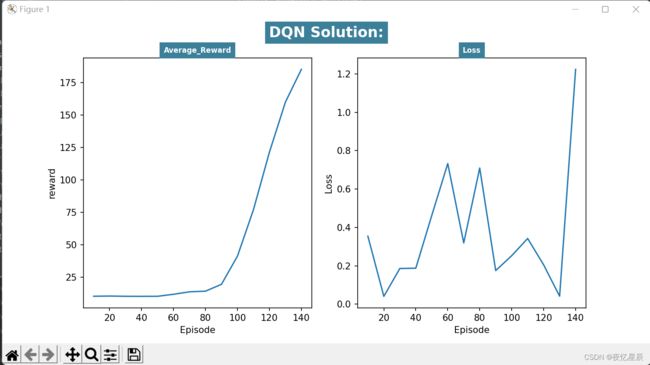
DQN(测试队列长为30,成功条件测试队列平均值≥195)
后面的数据看表格吧
整理分析如下表格
| 测试次数 | Episode | Average_reward | var | Time |
|---|---|---|---|---|
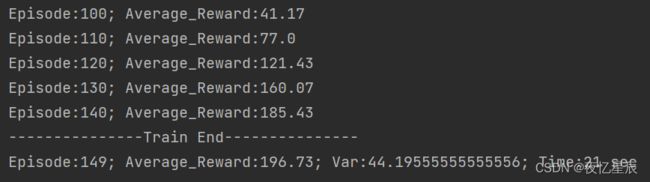
| 1 | 149 | 196.73 | 44.20 | 21 |
| 2 | 269 | 198.97 | 15.37 | 72 |
| 3 | 83 | 195.87 | 117.12 | 15 |
| 4 | 275 | 199.73 | 2.06 | 50 |
| / | / | 197.83 | / | / |
对于我写的这个DQN,有时候会出现一些较低 reward 情况,但是整体训练情况还是不错的,避免较低 reward 情况,测试队列设置为了30,基本就是1分钟内能出答案,方差基本都比较小,训练结果还是不错的。
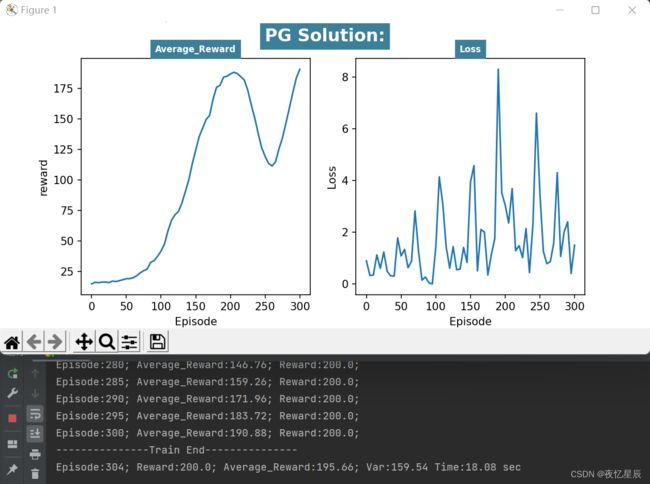
PG(测试队列长为50,成功条件测试队列平均值≥195)
整理分析如下表格
| 测试次数 | Episode | Average_reward | var | Time |
|---|---|---|---|---|
| 1 | 304 | 195.66 | 159.54 | 18 |
| 2 | 320 | 195.74 | 254.27 | 20 |
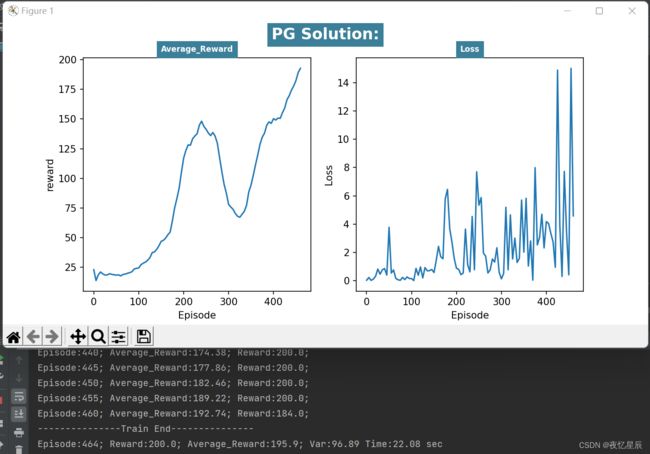
| 3 | 464 | 195.90 | 96.89 | 22 |
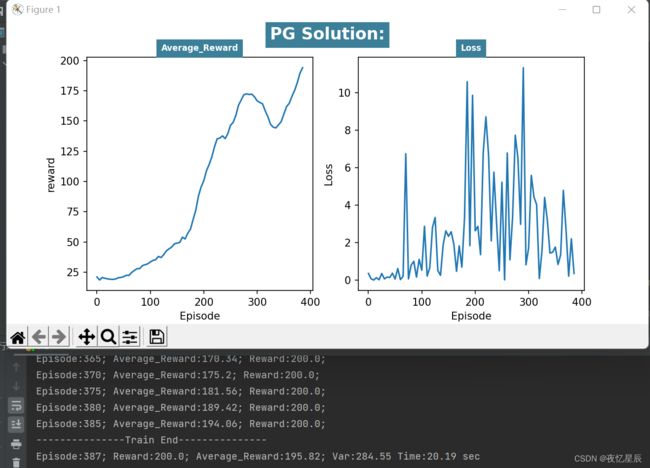
| 4 | 387 | 195.82 | 284.55 | 20 |
| / | / | 195.78 | / | / |
对于PG,同样有时候会出现一些较低 reward 情况,但是连续出现200得分是比较轻松的,测试队列设置为了50,基本就是20s左右能出答案,方差对比DQN比较大,(而且队列容量更大了)原因在于DQN中混杂有较差 reward 时,基本难以达到195的平均分,但是PG的200分比DQN更多,会导致含有较差 reward ,导致方差偏大,平均值偏小。
最后给PG提高难度。
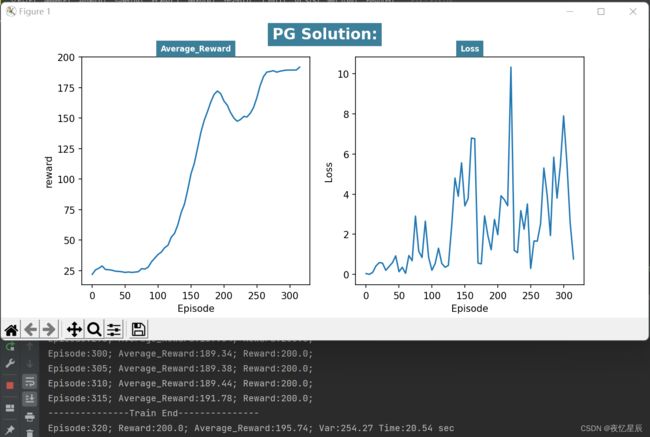
PG(测试队列长为30,成功条件测试队列平均值=200)
整理分析如下表格
| 测试次数 | Episode | Average_reward | var | Time |
|---|---|---|---|---|
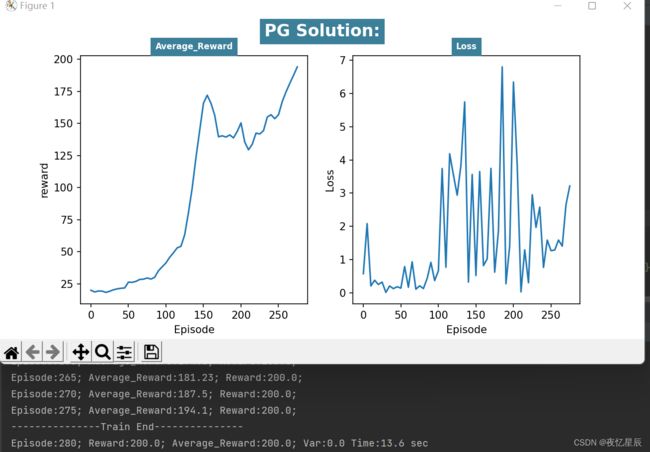
| 1 | 280 | 200 | 0 | 13.6 |
| 2 | 251 | 200 | 0 | 13.8 |
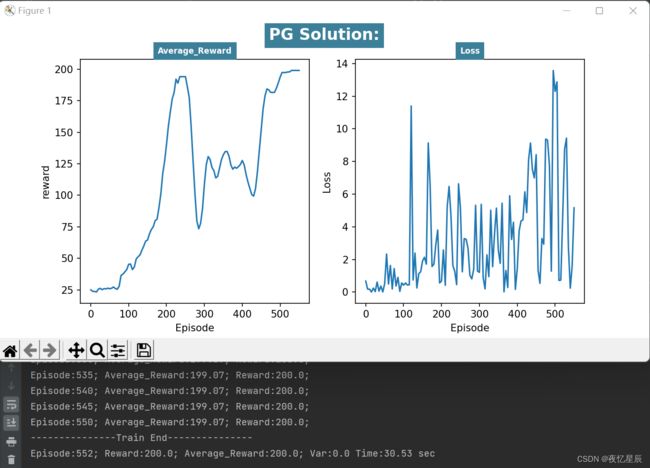
| 3 | 552 | 200 | 0 | 30.5 |
| / | / | 200 | / | / |
在同样的队列长度下(30),PG算法有着更好的表现,能够连续30次达到200,而DQN比较难做到这一点(时间会比较久)。
从 reward 函数曲线来看,一般都是先快速上升,在下降一段,在上升达到条件,这是由于有些动作选择的随机性导致的。
总结:DQN在Q-learning的基础上,结合DL进行值函数近似。DQN和Q-learning的很像,唯一不同的是,Q-learning存储Q值是通过Q表,DQN是通过值函数近似,用Q网络输出的值表示Q值。DQN的缺陷是过估计问题,就是其Eval-Q输出的Q值是高于其Q真实值的,根本原因在于Q值更新的公式中,利用Target-Q输出的最大值对应的动作为a',对于PG算法而言,优点在于与值函数相比,策略化参数的方法更简单,更容易收敛。缺点是策略搜索的方法更容易收敛局部极值点;在评估单个策略时,评估的并不好,方差容易过大。
四、 参考资料
强化学习—DQN算法原理详解binbigdata的博客-CSDN博客dqn算法
DeepRL系列(7): DQN(Deep Q-learning)算法原理与实现 - 知乎 (zhihu.com)
DIMA-PG算法原理 - 知乎 (zhihu.com)
OpenAI Gym 经典控制环境介绍——CartPole(倒立摆)思绪无限的博客-CSDN博客cartpole
如何调整DQN中的超参数
(1条消息) DQN调整超参数体会万德1010的博客-CSDN博客dqn调参
基于DQN算法解决Cart-Pole问题_高小喵的博客-CSDN博客
【动手学强化学习(1)DQN】CarPole DQN的实现 - 知乎 (zhihu.com)
pytorch教程之nn.Module类详解——使用Module类来自定义模型LoveMIss-Y的博客-CSDN博客pytorch 自定义module
pytorch源码阅读系列之Parameter类 - 知乎 (zhihu.com)
PyTorch中的parameters - 知乎 (zhihu.com)
torch.optim优化算法理解之optim.Adam()KGzhang的博客-CSDN博客torch.optim.adam
图解PyTorch中的torch.gather函数 - 知乎 (zhihu.com)
torch.unsqueeze() 和 torch.squeeze() - 知乎 (zhihu.com)
policy gradient解析