机器学习-支持向量机（SVM）

概述

支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane） 。
SVM使用铰链损失函数（hinge loss）计算经验风险（empirical risk）并在求解系统中加入了正则化项以优化结构风险（structural risk），是一个具有稀疏性和稳健性的分类器 。SVM可以通过核方法（kernel method）进行非线性分类，是常见的核学习（kernel learning）方法之一。

由简至繁的模型包括：

• 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机；
• 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机；
• 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机；

理论

线性分类

线性可分性（linear separability）
在分类问题中给定输入数据和学习目标：

其中输入数据的每个样本都包含多个特征并由此构成特征空间（feature space）

而学习目标为二元变量

表示负类（negative class）和正类（positive class）。

若输入数据所在的特征空间存在作为决策边界（decision boundary）的超平面将学习目标按正类和负类分开，并使任意样本的点到平面距离大于等于1。

则称该分类问题具有线性可分性，参数w,b分别为超平面的法向量和截距。
满足该条件的决策边界实际上构造了2个平行的超平面作为间隔边界以判别样本的分类：

所有在上间隔边界上方的样本属于正类，在下间隔边界下方的样本属于负类。两个间隔边界的距离

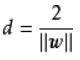
被定义为边距（margin），位于间隔边界上的正类和负类样本为支持向量（support vector）。

损失函数

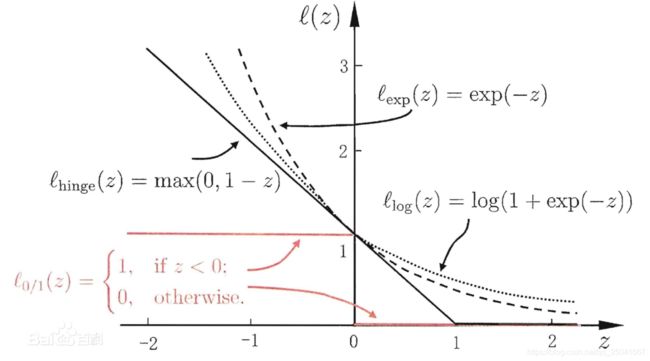
损失函数（loss function）在一个分类问题不具有线性可分性时，使用超平面作为决策边界会带来分类损失，即部分支持向量不再位于间隔边界上，而是进入了间隔边界内部，或落入决策边界的错误一侧。损失函数可以对分类损失进行量化，其按数学意义可以得到的形式是0-1损失函数：

0-1损失函数不是连续函数，不利于优化问题的求解，因此通常的选择是构造代理损失（surrogate loss）。可用的选择包括铰链损失函数（hinge loss）、logistic损失函数（logistic loss）、和指数损失函数（exponential loss），其中SVM使用的是铰链损失函数：

对替代损失的相合性研究表明，当代理损失是连续凸函数，并在任意取值下是0-1损失函数的上界，则求解代理损失最小化所得结果也是0-1损失最小化的解 。铰链损失函数满足上述条件。

核方法

一些线性不可分的问题可能是非线性可分的，即特征空间存在超曲面（hypersurface）将正类和负类分开。使用非线性函数可以将非线性可分问题从原始的特征空间映射至更高维的希尔伯特空间（Hilbert space），从而转化为线性可分问题，此时作为决策边界的超平面表示如下：

式中

为映射函数。由于映射函数具有复杂的形式，难以计算其内积，因此可使用核方法（kernel method），即定义映射函数的内积为核函数（kernel function）： 以回避内积的显式计算 。

Mercer定理（Mercer’s theorem）

核函数的选择需要一定条件，函数

是核函数的充要条件是，对输入空间的任意向量：

其核矩阵（kernel matrix），即如下形式的格拉姆矩阵（Gram matrix）：

是半正定矩阵。上述结论被称为Mercer定理 。定理的证明从略，结论性地，作为充分条件：特征空间内两个函数的内积是一个二元函数，在其核矩阵为半正定矩阵时，该二元函数具有可再生性：

因此其内积空间是一个赋范向量空间（normed vector space），可以完备化得到希尔伯特空间 ，即再生核希尔伯特空间（Reproducing Kernel Hilbert Space, RKHS）。作为必要条件，对核函数构造核矩阵后易知：

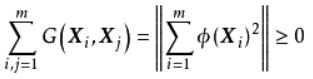
常见的核函数
在构造核函数后，验证其对输入空间内的任意格拉姆矩阵为半正定矩阵是困难的，因此通常的选择是使用现成的核函数 。以下给出一些核函数的例子，其中未做说明的参数均是该核函数的超参数（hyper-parameter）

当多项式核的阶为1时，其被称为线性核，对应的非线性分类器退化为线性分类器。RBF核也被称为高斯核（Gaussian kernel），其对应的映射函数将样本空间映射至无限维空间。核函数的线性组合和笛卡尔积也是核函数，此外对特征空间内的函数

也是核函数。

标准算法

线性SVM（linear SVM）

1. 硬边距（hard margin）

给定输入数据和学习目标：

硬边界SVM是在线性可分问题中求解最大边距超平面（maximum-margin hyperplane）的算法，约束条件是样本点到决策边界的距离大于等于1。硬边界SVM可以转化为一个等价的二次凸优化（quadratic convex optimization）问题进行求解 ：

由上式得到的决策边界可以对任意样本进行分类：

注意到虽然超平面法向量w是唯一优化目标，但学习数据和超平面的截距通过约束条件影响了该优化问题的求解。硬边距SVM是正则化系数取0时的软边距SVM，其对偶问题和求解参见软边距SVM，这里不额外列出。

2. 软边距（soft margin）

在线性不可分问题中使用硬边距SVM将产生分类误差，因此可在最大化边距的基础上引入损失函数构造新的优化问题。SVM使用铰链损失函数，沿用硬边界SVM的优化问题形式，软边距SVM的优化问题有如下表示：

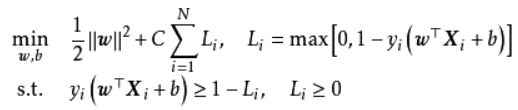
上式表明可知，软边距SVM是一个L2正则化分类器，式中Li表示铰链损失函数。使用松弛变量：ζ≥0 处理铰链损失函数的分段取值后，上式可化为：

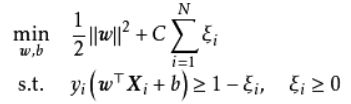
求解上述软边距SVM通常利用其优化问题的对偶性（duality），这里给出推导：
定义软边距SVM的优化问题为原问题（primal problem），通过拉格朗日乘子（Lagrange multiplier）：

可得到其拉格朗日函数 ：

令拉格朗日函数对优化目标w,b,ζ的偏导数为0，可得到一系列包含拉格朗日乘子的表达式 ：

将其带入拉格朗日函数后可得原问题的对偶问题（dual problem）：

对偶问题的约束条件中包含不等关系，因此其存在局部最优的条件是拉格朗日乘子满足Karush-Kuhn-Tucker条件（Karush-Kuhn-Tucker condition, KKT）：

由上述KKT条件可知，对任意样本(Xi,yi)，总有αi=0或yi(wTXi+b)=1-ξi，对前者，该样本不会对决策边界wTXi+b=0产生影响，对后者，该样本满足yi(wTXi+b)=1-ξi意味其处于间隔边界上（αiC），即该样本是支持向量。由此可见，软边距SVM决策边界的确定仅与支持向量有关，使用铰链损失函数使得SVM具有稀疏性 。

非线性SVM（nonlinear SVM）

使用非线性函数将输入数据映射至高维空间后应用线性SVM可得到非线性SVM。非线性SVM有如下优化问题：

类比软边距SVM，非线性SVM有如下对偶问题 ：

注意到式中存在映射函数内积，因此可以使用核方法，即直接选取核函数：

非线性SVM的对偶问题的KKT条件可同样类比软边距线性SVM。

数值求解

SVM的求解可以使用二次凸优化问题的数值方法，例如内点法和序列最小优化算法，在拥有充足学习样本时也可使用随机梯度下降。这里对以上3种数值方法在SVM中的应用进行介绍。

1. 内点法（Interior Point Method, IPM）

以软边距SVM为例，IPM使用对数阻挡函数（logarithmic barrier function）将SVM的对偶问题由极大值问题转化为极小值问题并将其优化目标和约束条件近似表示为如下形式：

式中I为对数阻挡函数，在本质上是使用连续函数对约束条件中的不等关系进行近似。对任意超参数 t，使用牛顿迭代法（Newton-Raphson method）可求解

该数值解也是原对偶问题的近似解：

IPM在计算

时需要对N阶矩阵求逆，在使用牛顿迭代法时也需要计算Hessian矩阵的逆，是一个内存开销大且复杂度为**O（N3）**的算法，仅适用于少量学习样本的情形 。一些研究通过低秩近似（low-rank approximation）和并行计算提出了更适用于大数据的IPM，并在SVM的实际学习中进行了应用和比较 。

2. 序列最小优化（Sequential Minimal Optimization, SMO）

SMO是一种坐标下降法（coordinate descent），以迭代方式求解SVM的对偶问题，其设计是在每个迭代步选择拉格朗日乘子中的两个变量αi,βi并固定其它参数，将原优化问题化简至1维子可行域（feasible subspace），此时约束条件有如下等价形式 ：

将上式右侧带入SVM的对偶问题并消去求和项中的αj可以得到仅关于αi的二次规划问题，该优化问题有闭式解可以快速计算。在此基础上，SMO有如下计算框架：

 1. 初始所有化拉格朗日乘子； 
 2. 识别一个不满足KKT条件的乘子，并求解其二次规划问题；
 3. 反复执行上述步骤直到所有乘子满足KKT条件或参数的更新量小于设定值。

可以证明，在二次凸优化问题中，SMO的每步迭代都严格地优化了SVM的对偶问题，且迭代会在有限步后收敛于全局极大值 。SMO算法的迭代速度与所选取乘子对KKT条件的偏离程度有关，因此SMO通常采用启发式方法选取拉格朗日乘子。

3. 随机梯度下降（Stochastic Gradient Descent, SGD）

SGD是机器学习问题中常见的优化算法，适用于样本充足的学习问题。SGD每次迭代都随机选择学习样本更新模型参数，以减少一次性处理所有样本带来的内存开销，其更新规则如下 ：

式中梯度前的系数是学习速率（learning rate），J是代价函数（cost function）。由于SVM的优化目标是凸函数，因此可以直接将其改写为极小值问题并作为代价函数运行SGD。以非线性SVM为例，其SGD迭代规则如下：

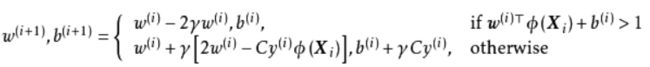
由上式可知，在每次迭代时，SGD首先判定约束条件，若该样本不满足约束条件，则SGD按学习速率最小化结构风险；若该样本满足约束条件，为SVM的支持向量，则SGD根据正则化系数平衡经验风险和结构风险，即SGD的迭代保持了SVM的稀疏性。