MATLAB数字图像处理 大作业:人脸表情识别

一、课程设计任务

运用已掌握的知识以及查阅相关资料，设计方案能够识别人脸表情中的高兴、厌恶、生气、悲伤、面无表情这五类表情。

二、课程设计原理及设计方案

2.1整体原理

本系统是基于PCA算法的人脸特征提取。运用PCA算法来实现人脸特征提取，然后通过计算欧式距离来判别待识别测试人脸。
整个系统的流程是首先是人面部的提取，这个人脸库里的人脸图像必须是格式及像素统一的，然后然后针对库里的人脸进行人脸训练，利用PCA进行人脸特征提取，获取特征矩阵向量组，将测试人脸投射到特征子空间中，运用欧氏距离，在人脸库里查找相应的人脸图像。并认为：与人脸库中欧氏距离最短的图像的标签所表示的表情为待测试图像所表示的表情，并输出。

2.2 PCA的基本原理

PCA中文全称主成分分析法（Principal Component Analysis）。掌握事物间主要区别的，运用统计学的分析方法，它可以使复杂的问题得到简化，找到物质之间的本质区别，用事物的主要影响因素来解决问题。计算主成分的主要目的是用来降维，也就把将高维空间数据降到低维空间中去。这种线性变化经常被用到数据的压缩和分析中。它就是以K-L变换为基础，运用它的正交变换可以降低数据的运算量。
在这个系统中，数据集内人脸读入后被变成为灰度数值图像，把这些数值矩阵按行或者按列排练构成一个原始图像空间，运用K-L变换有效的提取人脸图像的特征，这是为下面的小空间模式匹配奠定基础，这个原始图像空间是维数较高的矩阵，通过K-L变换后获得一组新的正交基。分析比较人脸训练样本中的一些统计特征，保留主要的特征向量，减少向量矩阵的维数，获得了维数较小的人脸空间。在参与训练的人脸样本中，一种是不一样人脸组成的总体散分布矩阵，另一种是同个人脸的不同表情的平均图片或者说是类间散布矩阵。第一种的运用对人脸图像的背景光线的要求很高，后者可以很好的避免光线带来的的干扰，且有减少计算量的作用。选择的正交基的原则是取大去小，所谓的大、小就是特征值的的大小，特征值的数值反应一个人脸的基本特征轮廓，在主要成分分析中就是以它主要能量特征值对应的向量来做基底，用这个方法可以很好的进行人脸重构，重构的人脸必须是参与算法的人脸图像，否则实现重建的效果较差。
通过降维后，就可以获得特征空间，将待识别人脸图像进行旋转变换，可以有效的降低维数。也就是用特征空间的向量的线性代数运算来表示。这样就可以把人脸识别这个过程转换成维空间坐标系数分类问题，至于如何分类可以采用简单的距离进行判断。在本实验中，采用欧氏距离进行判断。

2.3基于PCA的特征提取

PCA人脸识别特征提取有几个过程：人脸图像获取和处理；构造人脸库并且训练形成特征子空间；提取特征值和特征向量。下面对整个PCA提取特征过程中的步骤做一个详细的描述。

2.3.1人脸图像获取和处理，构造人脸库

通过拍照的方式，在背景设定的环境下，拍取人脸图像，然后对人脸样本采取前期的处理，其中包括人脸图像格式的变换，是否需要灰度处理等等。这些都要根据算法需求来对图像进行前期的预处理。PCA算法运用的统计学原理中的K-L变换的原理，对图像背景要求一致，而对光线的要求也一般，前期只要保证图像像素和格式一致就可以。最后保存图像，建立人脸库。

2.3.2 训练人脸库

人脸图像获取后，要放进人脸库，把人脸库统一配置后，选取每个人若干图片参与训练，变成训练矩阵。假定格式统一的人脸图像的像素为$nm$，采取变换转化为一维矩阵，然后按行相连构成$N=nm$维数的的矢量，每个人脸图像都可以视为$N$维空间中的一点，运用K-L变换可以将这个图像转换到底维的空间当中去，这样描述更加具体。

2.3.3 计算人脸图像的生成矩阵

采用训练后的人脸图像构成样本集，产生协方差矩阵可以用以下几种方法求出来。这三种方法是等价的。
$$\{\begin{array}{l}1.C_A=({\sum }_{k=1}^M\chi \cdot {\chi }^T)/M-m_x\cdot m_x^T\\ 2.C_A=(A\cdot A^T)/M\\ 3.C_A=[{\sum }_{i=1}^m[({\chi }_i-m_x)({\chi }_i-m_x{)}^T]/M\end{array}$$
协方差矩阵是一个大小为$N\ast N$的合成矩阵，其中$N$表示维数。 $A$表示每个人脸灰度图像减去平均人脸图像后按列构成的的矩阵，也是平均人脸图像。$M$表示人脸库内参与训练的人脸数。
鉴于公式的复杂性，一般选择第二个公式来计算人脸特征值和特征向量。

2.3.4 提取特征值和特征向量

在我们获得协方差矩阵后，需要求出其特征值和特征向量，由于PCA的理论基础是K-L变换，而我们所求的K-L变换的新坐标系是由$N\ast N$维的矩阵的特征值和特征量组成，直接求这两个参数难度高计算量非常大，下面介绍两种方法：
（1）奇异值分解原理
设$A\in R_r^{m\ast n}(r>0)$，则存在$m$阶正交矩阵$U$和$n$阶正交矩阵$V$，使得：
$U^{T}AV=\left(\begin{array}{cc}\Sigma & 0\\ 0& 0\end{array}\right)$
其中$\Sigma =\mathrm{diag}({\sigma }_1,{\sigma }_2,...,{\sigma }_r),{\sigma }_i=(1,2,...,r)$为矩阵$A$的全部非零奇异值，满足${\sigma }_1\ge {\sigma }_2\ge ...\ge {\sigma }_{\gamma }\ge 0$
前几个值较大，包含了矩阵$A$的大部分信息，$U$的列向量（左奇异向量）是$A{A}^T$的特征向量，$V$的列向量（右奇异向量）是$A^{T}A$的特征向量。
（2）小矩阵计算大矩阵特征向量原理
在求高维矩阵特征向量时，可以用统计学的方法，将它变换为求转化为求低维矩阵的特征向量：
设：$A$是一个秩为$r$的$mn(m\gg n)$维矩阵，是一个矩阵，现在要求的特征值以及特征向量，可通过先求小矩阵的特征向量和特征值 ，两者之间有以下关系：
$$\begin{gathered} A^{T}A\cdot v_i={\lambda }_i(A\cdot v_i) \\ A{A}^T(A\cdot v_i)={\lambda }_i(A\cdot v_i) \end{gathered}$$
显然，$C_A=A{A}^T$的特征向量是$A\cdot v_i$（没有单位化），$[{\lambda }_1,{\lambda }_2,...{\lambda }_{r-1}]$是它的特征值。
注意：以上两种求解协方差矩阵的特征值和特征向量的方法，结果是一致的。
2.3.5 相似性测度
人脸样本在用PCA算法获取人脸特征后，转换为特征空间内的一点。所以样本之间的区分性可以运用角度或者距离的计算来比较实现。常见的匹配的算法有夹角余弦、街区距离和欧式距离等等，下面具体的描述下欧式距离这个测度。
欧式距离的定义：欧式距离（Eudidean distance）是一个普遍使用的距离定义，它说明某种物质在多维空间的真实距离。欧式距离看作是衡量物质的相似程度的依据，两个点的距离差越小就越一样。
假如$x,y$是两幅维数一样的图像，它们的维数都是$MN$，则它在一个设定空间的表示如下：
$$\begin{gathered} x=(x_1,x_2,...,x_{kN+1},...,x_{MN}),k=[1,2,...,M] \\ y=(y_1,y_2,...,y_{kN+1},...,y_{MN}),k=[1,2,...,M] \end{gathered}$$
其中，$x_{kN+1},y_{kN+1}$为图像$x,y$的第$(k,1)$个像素点。则图像间的欧氏距离可表示如下为：
$$d_E(x,y)=[\sum _{k=1}^{MN}(x_k-y_k{)}^2{]}^{\frac{1}{2}}$$
在测试时，将测试图片与训练集图片一一比较，选用与训练集图片中欧氏距离最短的图片的标签（表情）为测试图片的表情。

三、课程设计步骤和结果

3.1步骤

3.1.1 整体步骤

1）找出表情为Neutral的图，根据LabelFile.txt识别。
2）读取文件，并将图像都压缩存储到一个变量之中。
3）提取脸部，去除背景，并把脸部区域存在img中。
4）求img每列均值meanImage=mean(img,2)。
5）PCA降维，提取特征（保留30个维度）。
6）对测试集同样提取均值（保留30个维度）。
7）根据这30个维度计算与面无表情训练图像的欧氏距离。
8）分别对比每个图像与训练集每个图像的欧式距离，欧氏距离最短的训练集图像的表情即为需要测试的图像的表情

3.1.2 脸部ROI提取步骤

本流程为章节3.1中整体步骤中第三步的展开。
1）转换颜色空间RGB为亮度色度空间YCbCr。
2）把10 3）去噪：用形态学操作填补连通区域中的空洞，可能会识别到多个区域。
4）对于每一个连通域，提取轮廓，认为轮廓面积最大的连通区域才是人脸，其余区域舍弃。
5）将第2、第3、第4步骤中获取得到的掩膜与输入图像原图相乘，得到需要在后续步骤中识别表情的人脸区域。

3.1.3 步骤优化

在3.1章节的步骤中，每次需要测试新的图像时，都需要将训练集中的图像重新读取、重新进行训练，在matlab环境中此训练存在一定的耗时且不必要。本课程设计使用到的特征提取类似于机器学习/深度学习但又不是机器学习/深度学习，可以用matlab工作区文件的形式将训练得到的结果与“模型”存储下来，在测试时直接读取该文件中存储的“模型”。因此，可以对3.1章节的步骤进行适当的修改与优化处理，将训练与测试的流程进行分离。
训练的流程如下：
1）找出表情为Neutral的图，根据LabelFile.txt识别。
2）读取文件，并将图像都压缩存储到一个变量之中。
3）提取脸部，去除背景，并把脸部区域存在img中。
4）求img每列均值meanImage=mean(img,2)。
5）PCA降维，提取特征（保留30个维度）。
6）将特征提取完毕并将训练结果以matlab工作区文件的形式进行存储。
测试的流程如下：
1）读取文件，并将图像都压缩存储到一个变量之中。
2）提取脸部，去除背景，并把脸部区域存在img中。
3）读取由训练流程第6）步所得到的matlab工作区文件。
4）对测试集同样提取均值（保留30个维度）
5）根据这30个维度计算与面无表情训练图像的欧氏距离。
6）分别对比每个图像与训练集每个图像的欧式距离，欧氏距离最短的训练集图像的表情即为需要测试的图像的表情。
对步骤进行优化后的函数调用关系如下图所示：

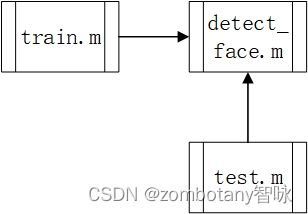
流程图如下图所示：

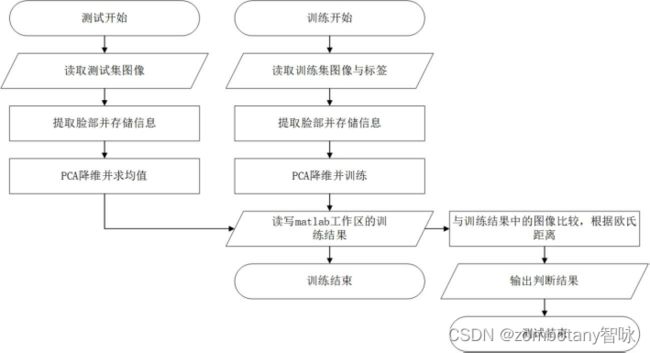
3.2 结果

3.2.1 单个测试

【为保护个人隐私，用于测试的真人图像已略去】
如图，利用真实拍摄的人脸图像进行测试。上图为提取人脸部分的流程。对于输入图像，检测颜色。在YCbCr空间中，检测Cr>10的部分初步认为是人脸。此时，手与真正的脸部主体的颜色都被检测到，并被初步认为是人脸。接着，利用去噪并提取轮廓、增强轮廓信息、填充空洞等较为传统的形态学操作算法填补脸部空洞（如眼睛、眼睛等区域），并很好地填补、去除了噪声区域。检测连通域面积，认为连通域面积最大的部分才是人脸。如上图的第6个子图所示，人脸被提取出并返回给运行测试的主函数。

测试的结果以文件的形式输出，可以看到这一真实拍摄的照片的表情被认为是“neutral”（面无表情），分类较为正确。
【为保护个人隐私，用于测试的真人图像已略去】
使用另一张真实拍摄的图片进行测试，这一图片比上一张图片的情况更为简单，不存在多个YCbCr颜色空间中Cr>10的连通域。提取人脸的步骤不再赘述。

可以看到这一表情被正确地识别为“sad”,即不高兴。

3.2.2测试集结果

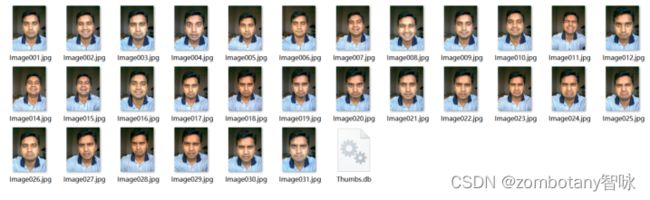
仅仅使用一两张测试图像不能很好地衡量表情识别的准确性。在下载训练集时，也附带了一些没有标签、待测试的数据集。测试结果如上图所示。数据范围较小，只有30张图片，我们可以人工地对数据集中的图片进行分类，并于测试结果比较。得到的混淆矩阵如下，并将查全率与查准率附在混淆矩阵中：

		预测	预测	预测	预测	预测	查全率（recall）
		面无表情	高兴	恶心	愤怒	沮丧
实际	面无表情	4	1	0	0	0	80%
实际	高兴	0	4	0	0	2	66.7%
实际	恶心	0	0	11	0	0	100%
实际	愤怒	0	0	0	4	0	100%
实际	沮丧	0	0	1	1	1	33%
	查准率（precision）	100%	80%	91.6%	80%	33%

可以从混淆矩阵中看到，尽管存在一定误分类的情况，但对大多数类型的表情的识别都是较为准确的。

四、课程设计总结

五、设计体会

参考文献

[1]何东健.数字图像处理[M].西安电子科技大学出版社，2009年.
[2]阮秋琦.数字图像处理[M].电子工业出版社，2001年.
[3]徐建华.图像处理与分析[M].科学出版社,1999年.
[4]徐中立.数字图像的智能信息处理[M].科学教育出版社，2001年.

源代码与数据集

https://download.csdn.net/download/sinat_36321918/10742127
参考的是这个，本文以此为基础进行的魔改并对原理进行了一定研究与讲解。为了防止侵权并为了防止隐私泄露，不放出自己魔改的测试集与代码。需要的可以私聊或邮件。