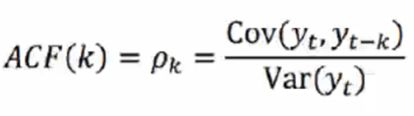异常检测&动态阈值

一.常规方法：

分析历史数据或窗口数据的均值、中位数、众数分布，选择算法。

 

算法流程：

• 绝对中位差

绝对中位差，即Median Absolute Deviation(MAD)，是对单变量数值型数据的样本偏差的一种鲁棒性测量。在先验为正态分布的情况下，一般C选择1.4826，k选择3。

应用：根据历史数据(例如近一个月)的绝对中位差，计算上下限值。使用上下限值作为当前的上下阈值。

• 箱形图

箱形图主要通过几个统计量来描述样本分布的离散程度以及对称性，包括：

• Q0：最小值（Minimum）
• Q1：下四分位数（Lower Quartile）
• Q2：中位数（Median）
• Q3：上四分位数（Upper Quartile）
• Q4：最大值（Maximum）

将Q1与Q3之间的间距称为IQR，当样本偏离上四分位1.5倍的IQR（或是偏离下四分位数1.5倍的IQR）的情况下，将样本视为是一个离群点。

应用：根据历史数据(例如近一个月)计算IQR，1.5倍的IQR上下限值。使用上下限值作为当前的上下阈值。

• 极值理论

极值理论[8]是在不基于原始数据的任何分布假设下，通过推断我们可能会观察到的极端事件的分布，这就是极值分布（EVD）。

应用：不适合

二.周期时序预测方法：

自回归系列

自回归（Auto Regression）为传统的时间序列，其中涵盖：ARMA、ARIMA、ARCH等模型。此种方式的统计学原理比较简单，所以在预测的场景中也是比较通用。

ARIMA模型

ARIMA（p，i，q）模型全称为差分自回归移动平均模型（Autoregressive Integrated Moving Average Model）

ARIMA首先要确定差分阶数i，以确保数据在i阶差分后平稳；接着，再确定是AR（q=0）、MA（p=0）还是ARMA（p、q均不为0）。参数p、q可以通过ACF图与PACF图选定。

差分法（求i）

差分法：时间序列在t与t-1时刻的差值。

自回归模型 （AR）

描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。

移动平均模型 （MA）

移动平均模型关注的是自回归模型中的误差项的累加。移动平均模型能够有效的消除预测中的随机波动。

自相关函数ACF（Autocorrelation Function）

有序的随机变量序列及其自身比较。自相关函数反应了同一序列在不同时序的取值之间的相关性。

偏自相关函数（PACF）（Partial Autocorrelation Function）

对于一个平稳的AR（q）模型，求出滞后k自相关系数p(k）时，实际上得到的并不是x(t)与x(t-k)之间的单纯的相关关系。x(t)同时还会受到k-1个随机变量x(t-1)、x(t-2)、…x(t-k-1)的影响，而这k-1个随机变量又都和x(t-k)具有相关关系，所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响

偏自相关函数（PACK）剔除了中间k-1个随机变量的干扰。ACF还包含了其他变量的影响，而偏自相关系数PACF是严格这两个变量的相关性。

ARIMA（p，i，d）阶数确定

拖尾： 始终有非零取值，不会在大于某阶后就快速趋近于0（而是在0附近波动），可简单理解为无论如何都不会为0，而是在某阶之后在0附近随机变化。

截尾： 在大于某阶(k)后快速趋于0为k阶截尾，可简单理解为从某阶之后直接就变为0。

ARIMA建模一般步骤：

① 首先需要对观测值序列进行平稳性检测，如果不平稳，则对其进行差分运算直到差分后的数据平稳；
② 在数据平稳后则对其进行白噪声检验，白噪声是指零均值常方差的随机平稳序列；
③ 如果是平稳非白噪声序列就计算ACF（自相关系数）、PACF（偏自相关系数），进行ARMA等模型识别；
④ 对已识别好的模型，确定模型参数，最后应用预测并进行误差分析。

「自回归系列」方式弊端

1..适用的时序数据过于局限
其要求时序数据是稳定的，或者通过差分化后是稳定的，且在差分运算时提取的是固定周期的信息。这往往很难符合现实数据的情况。

2、仅适用于短期预测，对于中长期表现不佳

3、无法处理由于节假日、特殊时点（例如：双十一）等带来的变点问题

4、模型的解耦能力较差，无法分析出影响准确率的潜在因素

Prophet模型

• 训练数据：拥有至少一个完整周期的数据，让模型完整学习规律。
• 数据趋势：数据有一定正常的周期效应，例如：周末效应、季节效应等。
• 跳变情况：明确可能发生跳变的时间点及窗口期，例如：双十一、国庆节等。
• 缺失值符合预期：历史数据的缺失值和异常值保持在合理范围内。

Prophet可将趋势项、周期项、节假日项解耦开来，因此该模型也是由这三者，加上噪声项组合而成，如下图：

• g(t) 表示趋势项，它表示时间序列在非周期上面的变化趋势；
• s(t) 表示周期项，或者称为季节项，一般来说是以周或者年为单位；
• h(t) 表示节假日项，表示时间序列中那些潜在的具有非固定周期的节假日对预测值造成的影响；
• 即误差项或者称为剩余项，表示模型未预测到的波动， 服从高斯分布；

弊端：

1. 趋势项需要识别并设置变点，难以确认，通过默认设置的参数，存在不确定性

2.上线阈值是基于趋势的不确定性，通过设置窗口宽度进行生成的，上下阈值趋势是一致的。

lower_p = 100 * (1.0 - self.interval_width) / 2； upper_p = 100 * (1.0 + self.interval_width) / 2

算法	算法类型	支持预测基准值	支持预测动态阈值	检测周期性	添加特殊日期	数据要求
3Sigma	分布与统计	是	是	否	否	服从正太分布、平稳
绝对中位差	统计	是	是	否	否	服从正太分布、平稳
箱型图	统计	是	是	否	否	平稳
ARIMA/SARIMA	统计	是	是	是	否	平稳
Prophet	统计	是	是	是	是	存在完整周期
Xgboost	机器学习
LSTM	深度学习

参考：

基于AI算法的数据库异常监测系统的设计与实现 - 美团技术团队

时间序列预测——ARIMA模型_白天数糖晚上数羊的博客-CSDN博客_arima模型预测

https://facebook.github.io/prophet/docs/diagnostics.html#cross-vali