基于点、线数据三维地质建模方法

**

基于点、线数据三维地质建模方法

**

1.前言

  作者本人计算机出身，近一年多负责公司地质建模项目项目工作，项目关联计算机、采矿行业相关技术。本文章主要介绍采矿行业地质建模及模型更新相关数字化自动更新技术，不专业之处，请谅解。下图为本人设计开发的地质建模整模块，后续将会详细讲解各模块功能。

2.简介

  何为矿体建模？何为隐式建模？
  矿体建模的对象是矿体结构模型。我们根据表达方式的不同将矿体建模方法分为两大类型：显式建模与隐式建模。显式建模方法采用网格模型来显式表达矿体的几何模型，首先确定剖面，并在剖面上绘制岩性、断层和矿脉，然后手工地绘制剖面连线来连接跨多个截面的曲面，这种方式建立地质模型既耗时又不灵活，因为当有更多数据可用时，很难更新模型。隐式建模方法则采用隐式函数来隐式表达任意复杂矿体的几何模型，隐式模型很容易跟上最新数据。新的钻孔数据可以快速集成，而不是花费数周或更长时间手动修改模型。这里的“隐式”有两重含义：一是指采用隐式函数来表示三维模型；另一个是指采用函数所表示的三维模型不能直接在三维视图中进行显示，需要通过曲面重构的方法转化为网格模型来显示。
  隐式建模方法是一种非常适合于构造交互式约束条件的方法，其建立的模型动态更新较为方便。该方法将基于不同地质数据所构造的几何空间通过距离函数转换为隐式函数场，以数学函数的方式表达三维模型，所重构的曲面被表示为隐式函数的零水平集。由于创建模型所需的工作量较小，因此有更多的时间用于了解地质情况和研究更复杂的细节，如断层、地层序列、趋势和矿脉。这个模型可以发展成比以前更精确地反映现实。
  矿体模型的隐式表达还具有以下优点：可以根据需要生成不同尺度的高质量三维模型；可以通过调整约束规则或获得一系列不同的建模结果；可以对多种不同类型的地质数据同时进行建模；可以融合多域模型且保证模型间较好的接触关系，其中一个很好的应用是模型直接的布尔运算变得非常容易；可以融合多种不同方法建模的结果，其中一个很好的应用是可以将显式建模的结果融合到隐式建模中；可以隐式存储表征矿体模型的插值函数而不是需要占用大量存储空间的网格模型。

3.行业优势

  地质隐式建模对比于显式建模能够快速地得到地下要素信息的三维可视化表达，直观展示地下不规则分布的地质体几何结构，实现大量钻孔及剖面数据实时动态更新矿体模型。帮助地质工作者形象直观地分析地质特征并处理大量的野外测量和样品分析数据，有效地指导矿业生产，提高建模效率，降低建模成本。

4.基本流程

（1）采样数据
  采样数据涉及的数据类型较为广泛，包括在地质勘探和生产勘探中获得的原始采样数据以及人工解译的轮廓线信息。其中涉及到勘探钻孔数据采用样品组合的方法根据工业指标对钻孔进行矿段组合，得到界定矿体边界的样段和非样段数据，而人工解释的数据可以转化为点、线数据作为原始数据处理。下图为实际应用中点、线数据可视化表达形式（必须承认有参考国际上较为先进的地质建模软件如LeapFrog等）。

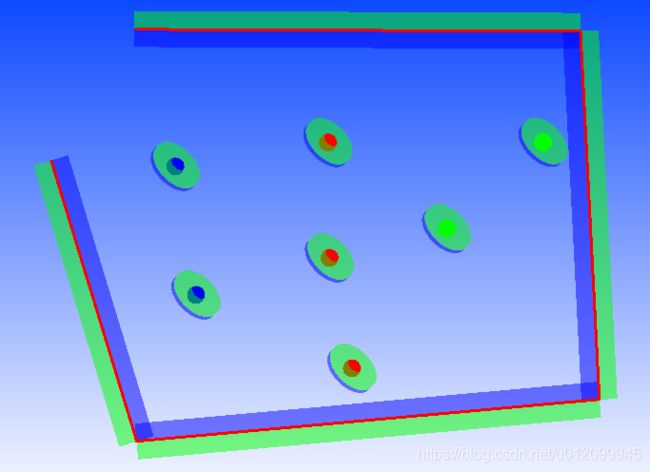
（2）建模数据
  建模数据主要分为三类：约束数据、插值数据和建模参数。约束数据由各种约束规则构造，例如模型生成外包、边界、各向异性趋势等。插值数据由可以直接用于计算生成模型的数据构成，如前文中的点、线数据。建模参数则包含一些地质规则参数，如基台、块金、漂移等。
（3）模型数据
  目前根据初始地质数据的不同可以将矿体隐式建模方法分为两大类：基于钻孔数据的矿体隐式建模方法和基于人工解释点、线数据的矿体隐式建模方法。
  适合于对具有几何边界约束直接基于钻孔数据的隐式建模方法建模流程具体步骤描述如下图：

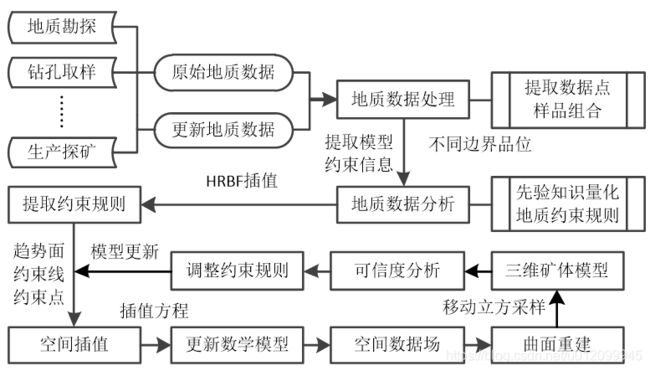
  基于人工解释点、线数据的隐式建模方法建模流程具体步骤描述如下图：

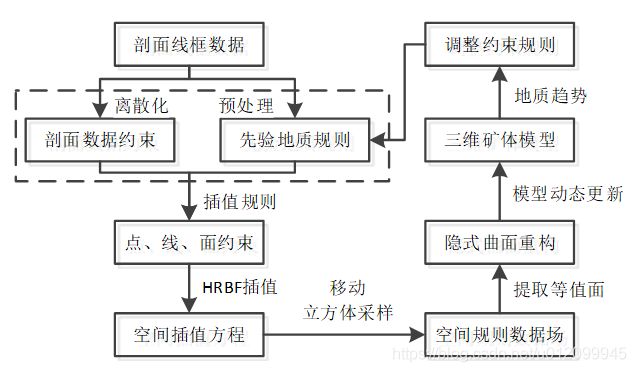
5.算法求解

  矿体隐式建模方法使用满足各种地质规则约束的隐式函数来表示矿体模型。基于不同地质数据的矿体隐式建模方法的主要思路：首先，通过离散化的方式按一定的采样粒度将相应类型的地质数据转化为各种不同的插值约束；其次，通过求解插值约束所构造的插值方程来获得表征矿体模型的隐式函数；最后，利用等值面提取方法重构出表征矿体模型的隐式函数。基本原理如下图所示。

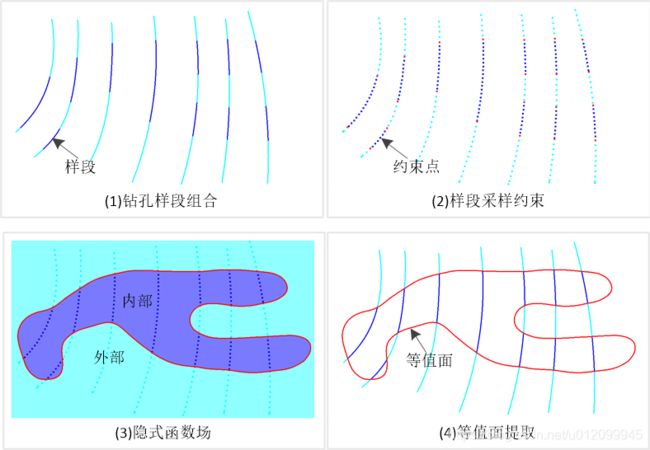
  为了恢复任意复杂的矿体模型，通常可以在某个函数空间中寻找一组基函数来逼近表征矿体模型的未知连续函数。
  在地质体数据不足的情况下，利用空间插值方法实现数据的网格化，推断并预测未知区域及研究较少区域的地质体信息的分布趋势，利用三维曲面重建算法及三维可视化技术相结合，能有效对不规则勘查数据自动实现地质要素的三维形态模拟。
  采用空间插值算法，可以大幅提高建模自动化的程度，空间插值的过程是一个输入一些观察的数据点，输出反应这些数据规律的函数y=f(x)的过程。
  目前应用于地质领域的空间插值与拟合方法有许多种，其中常用的主要有：距离反比插值法，改进谢别德法，克里金插值法，径向基函数法，最小曲率法，Voronoi图，最近邻点插值法，多元回归法，局部多项式法，线性插值法以及趋势面法等。
  对于局部插值方法，如果某个子域内的约束不影响其他子域内的约束，则该子域内的求解结果与其他子域内的求解结果相互独立。由于该子域内的更新约束只能影响邻近的约束，意味着更新约束不会影响非邻近约束的权重，这些更新约束对子域外势场的插值也就不会变化。因此，在动态更新时，该子域内的约束可以单独进行求解。
  对于全局插值方法，迭代求解的迭代过程一般要求指定初始解。如果选择的初始解不合适，则迭代过程可能不会收敛或收敛缓慢。通常选择零值的平凡向量作为初始解，以确保较小的相对误差。对于矿体的隐式建模，随着约束的逐步添加，RBF方程将被重复求解多次。在实验的过程中，我们发现只要新添加约束的数量足够小，当前的求解结果接近于上次的求解结果。因此，可以考虑通过已有解的结果来确定初始解，以提高矿体模型更新时的收敛速度。
  常见的插值方法包括径向基函数插值方法，径向基插值函数()具有以下形式。

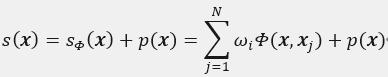
  其中={1,2,…,}是一组各不相同的插值中心，是待确定的权重系数。(,)是一种径向基核函数。 ()为核函数部分，()为多项式部分，设{1,2,…,}为相应多项式空间中的一组基。
  径向基插值函数 ()通常用于插值域约束。

  其中为势场的函数值。
  对于径向基类函数插值的方法，可以在任意采样位置通过插值约束来定义势场域值和势场方向类型的约束。一般的径向基函数插值所考虑的约束点信息中只包含函数值，而Hermite型的径向基函数插值（HRBF）方法则可以考虑约束点信息中包含函数导数值的情况。在HRBF插值方法中，最明显的改变是可以通过较强的法向约束代替较弱的离面约束，避免在局部产生二义性的离面约束，使得在不容易表达离面约束的地方具有较好的几何约束特征。而广义径向基函数插值方法则是更一般的插值方法，可以融合更多类型的插值约束，比如用于限制插值趋势的切向约束。

6.模型重构

  尽管可以采用函数来隐式表达矿体模型，但这种模型表达方式是不可视的且一般不能直接应用于矿山开采设计中。因此，需要根据实际应用的需要对抽象的隐式函数进行曲面重构以得到网格化的隐式模型。在隐式函数求解的基础之上，可以根据曲面重构的方法获得多精度的矿体网格模型。为了高效地重构出隐式函数所表征的矿体模型，需要采用快速的隐式函数评估方法和曲面追踪方法。对于具有大规模约束的径向基函数插值问题，可以考虑将评估和重构过程结合起来加速隐式曲面的重构。
  隐式曲面重构的基本思路是采用离散化的多边形（Polygon）来逼近连续的隐式函数。为了获得离散化的多边形，首先需要对模型所在的几何空间进行离散化采样，并利用求解的隐式函数评估采样点处的函数值，以便基于已有的采样点插值未知隐式曲面所在等值面上的近似点。然后采用多边形按一定的拓扑关系组合后形成的网格模型来近似表达连续的隐式曲面。基于以上分析，隐式曲面重构的过程主要分为三步：离散化采样、采样点评估和网格模型生成。
  地质体三维曲面重构算法。基于三维空间规则数据场构建三维曲面的方法很多，典型的有采用三维等值面构建算法实现由网格离散点到三维等值面的模拟，实现三维曲面重建。以Marching Cubes算法是一种三维数据场等值面提取的经典算法，但在对复杂地质体建模时，其建模重构效率等方面还存在一些问题，因此，目前有许多学者在进行基于MC方法的重构优化方法研究。
  隐式函数的函数值符号表征了地质域内矿体模型的内外关系。地质域中任一点的函数值定义为该点到隐式曲面上最近点的距离。我们约定隐式曲面外点的函数值为正，隐式曲面内点的函数值为负。隐式函数值和隐式表面之间的关系可以表示为
  根据采样点构造的有符号距离场中，以有符号的隐式函数F§表示采样点与模型隐式曲面的最近距离，如图 7所示，其中位于隐式曲面内部的点为“负值”，外部点为“正值”，由零值点所确定的零水平点集即为模型的隐式曲面。也即对于三维空间中的任意点P，三维隐式曲面与隐式函数F§之间的关系可以表示为：

在三维空间中隐式曲面与函数值关系示意如下图。

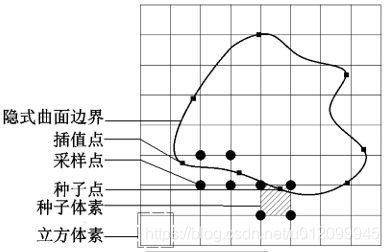
各项术语示意图如下。

7.实际应用

  隐式矿体建模实际效果展示如下图。

  隐式脉状超薄矿体建模实际效果展示如下图。

8.总结

  纵观全球地质建模软件的发展，行业龙头LeapFrog在20年前就着手研发，而Surpac、DataMine等也都集中团队力量在地质建模技术上开始着力。
  国内地质建模软件基本还处于萌芽阶段，目前整个地质建模模块已进入生产试运行阶段，随着国内数字化和智能化建设的加快，以及投入的不断增加，国内的地质建模软件也会追随前人的脚步前进。毕竟很多事情我们都将“站在巨人的肩膀上”。
  感谢一些同事尤其是中南大学采矿及地质同学大力支持。谢谢各位观看。

参考

[1] 钟德云. 地质规则约束下矿体隐式模型的快速重构与动态更新[D]. 长沙: 中南大学, 2020.
[2] 张炬,钟德云,王李管,王晋淼. 基于隐式函数的三维建模方法、装置、系统及存储介质[P]. 湖南省：CN110033519A,2019-07-19.