2022.12.4 第三十三次周报
目录
前言
文献阅读:结合循环神经网络和图神经网络来预测下一个地方的类别
背景
提出想法
本文主要贡献
POI-RGNN 架构
OGS-POI:对PoI进行分类
结论
RNN预测sin函数
pytorch之RNN参数解释
问题1:input_size 是什么?
问题3:num_layers是什么?
代码
运行结果
总结
前言
This week studied an article that combines recurrent neural networks and graph neural networks to predict the category of the next place.In this work, we propose an architecture to use GNNs to assist RNNs in a sequential problem of human mobility, particularly the problem of predicting the next PoI category that an individual is likely to visit. In addition, in terms of deep learning, it was learned to use RNNs to predict trigonometric functions.
本周学习了一篇结合循环神经网络和图神经网络来预测下一个地方的类别的文章。在这项工作中,作者提出了一种架构,使用GNN来帮助RNN解决人类流动性的顺序问题,特别是预测个人可能访问的下一个PoI类别的问题。除此之外,在深度学习方面,学习了用RNN来预测三角函数。
文献阅读:结合循环神经网络和图神经网络来预测下一个地方的类别
-Cláudio G.S. Capanema, Guilherme S. de Oliveira, Fabrício A. Silva, Thais R.M.B. Silva, Antonio A.F. Loureiro,
Combining recurrent and Graph Neural Networks to predict the next place’s category,
Ad Hoc Networks,
Volume 138,
2023,
103016,
ISSN 1570-8705,
https://doi.org/10.1016/j.adhoc.2022.103016.
背景
智能手机和平板电脑等移动设备的大量使用提高了大量移动数据的可用性。应用程序通常利用用户的位置来提供基于位置的个性化服务,例如移动辅助和地理围栏。此外,移动服务提供商一直在收集地理空间数据,以了解他们的用户并为他们提供更好、更个性化的服务。
地理空间数据也与智慧城市和城市交通概念密切相关。从这种数据类型中,可以了解个人和集体的人类流动模式,预测道路交通,估计应用程序的使用需求,并帮助城市规划,了解用户的移动模式和需求对于设计将成为智慧城市一部分的未来智能交通系统(ITS)至关重要。
提出想法
预测下一个兴趣点(PoI)的类别,一个经常访问的位置,是了解人类流动性的一项基本任务,因为现有地点类别的多样性激励个人从一个位置到另一个位置。递归神经网络(RNN)已被用于处理许多不同的问题中的人类移动数据。然而,图神经网络(GNN)在提高移动性问题的性能方面具有巨大的潜力,因为图能够根据它们之间的关系聚合不同元素的特征。例如,节点可以在图结构中表示PoI或街道交叉口,而边表示PoI之间连续访问的频率或街道交叉口之间的流动。此外,重要的是要注意,实体/节点之间的关系及其在非欧几里得空间中的特征被GNN而不是其他技术(如CNN(卷积神经网络)很好地捕获。
本文主要贡献
在这项工作中,我们提出了两个贡献,它们显着提高了性能,并为使用图神经网络的人类移动性问题创造了新的方向。
因此,这项工作的具体贡献总结如下:
1.我们提出了一种新颖的方法,该方法在人类移动的背景下结合了循环神经网络和图形神经网络,这是一个经常与顺序数据和循环模型相关的领域。特别是,我们的目标是预测移动用户的下一个访问地点的类别。与以前的研究不同,POI-RGNN模型认为循环组件捕获个人的最近行为(即访问地点的顺序数据),而图形组件捕获他/她的一般行为(即,在图形中聚合的历史移动性)。此外,它还为尚未探索的循环组件和图形组件添加了新输入。所提出的架构方便地结合了不同的元素并添加了特定的操作。
2.与现有研究不同,我们提出的POI-RGNN在两个不同的数据集上进行了评估:基于LBSN和基于原始GPS的数据集,我们分析了其在不同情况下的有效性。此外,我们将我们的提案与五种最先进的解决方案进行了比较。
3.我们提出了OGS-POI模型来对基于GPS的原始数据集的PoIs类别进行分类。从这个意义上说,我们不仅可以使用基于签入的数据集,还可以使用基于原始GPS的数据集来更好地评估POI-RGNN。OGS-POI包括两种不同的方法:第一种方法对用户特定的类别(即家庭和工作)进行分类,第二种对一般类型的类别(即购物,社区,食品,娱乐,户外旅行和夜生活)进行分类。据我们所知,这是第一部使用离线策略注释个人和一般类别地点的作品。
4.OGS-POI模型包括我们提出的用于对一般类别进行分类的神经网络的建议,称为PGC。它的架构探索了图神经网络的新节点特征矩阵,并包括两个代表数据不同视图的组件:用户和集体。因此,该模型可以根据当前用户和其他用户的访问方式更好地预测 PoI 类别。我们利用来自标记良好的域的迁移学习,因此需要来自原始 GPS 数据集的最少数量的标记数据。
POI-RGNN 架构
所提出的模型方便地结合了循环神经网络和图形神经网络,以预测要访问的下一个PoI的类别。
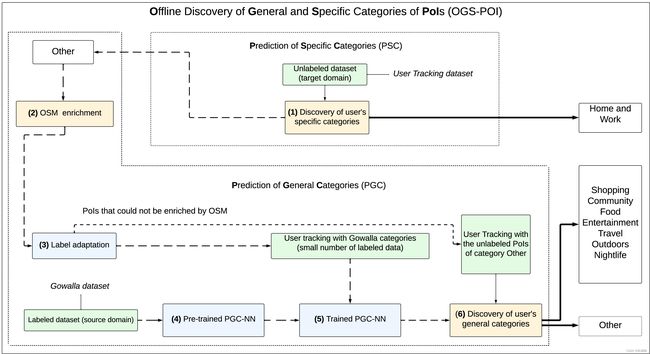
OGS-POI:对PoI进行分类
PoI分类问题旨在发现个人访问的每个PoI的类别。由于在许多情况下,缺乏基于GPS的位置数据提供的信息,特别是在PoI类别方面,我们需要提供一种方法来丰富PoI的语义。此任务的目标是通过从标记良好的数据集传输知识来更好地注释未标记数据集的 PoIs 类别。
结论
在这项工作中,我们提出了一种架构,使用GNN来帮助RNN解决人类流动性的顺序问题,特别是预测个人可能访问的下一个PoI类别的问题。所提出的模型包含最先进的主要方法,如GRU,多头注意力和GCN层,同时使用不同的输入。GNN 组件背后的原因是捕获每个用户的一般移动行为,用图形表示。因此,它可以在我们的顺序问题中帮助RNN组件。此外,我们的提案以循环和图形方式利用基于空间和时间的输入。特别是,顺序和图形输入告知神经网络类别之间的转换在空间和时间上的稀疏程度。所提出的架构在基于签到或原始GPS数据的数据集中被证明是有效的。我们还建议,结合GNN和RNN可以使与人类流动性相关的其他问题受益。
为了丰富基于GPS的原始数据集的PoI,我们提出了OGS-POI,这是一种用于发现特定和一般类型的PoI类别的离线方法。与现有解决方案相比,我们的模型具有离线和预测各种地点类别的优势。OGS-POI方法中包含的拟议PGC-NN包括新的节点特征矩阵,用于联合和单独生成与工作日和周末数据相关的嵌入。它还提供用户和集体对用户访问过的地方的看法,以生成最终预测。
RNN预测sin函数
pytorch之RNN参数解释
问题1:input_size 是什么?
说白了input_size无非就是你输入RNN的维度,比如说NLP中你需要把一个单词输入到RNN中,这个单词的编码是300维的,那么这个input_size就是300.这里的input_size其实就是规定了你的输入变量的维度。用f(wX+b)来类比的话,这里输入的就是X的维度。
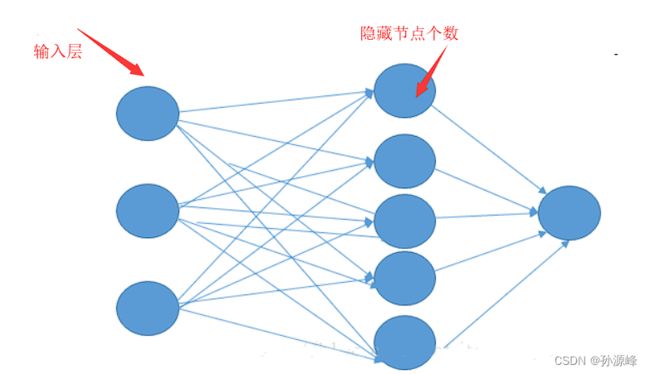
问题2:hidden_size 是什么?
和最简单的BP网络一样的,每个RNN的节点实际上就是一个BP嘛,包含输入层,隐含层,输出层。这里的hidden_size呢,你可以看做是隐含层中,隐含节点的个数。
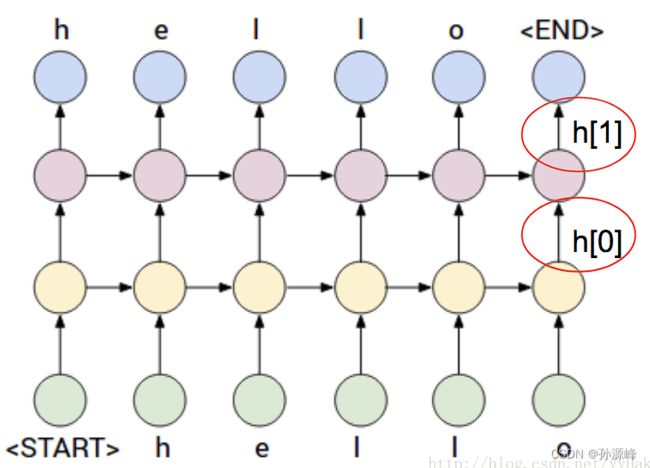
问题3:num_layers是什么?
如果num_layer=2的话,表示两个RNN堆叠在一起。
举例来说
如果是num_layer==1的话
如果num_layer==2的话
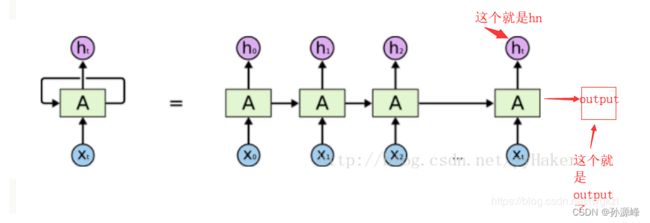
问题4:hn(hidden),output分别是什么?
hidden的输出size为[ num_layers* num_directions, batch_size, n_hidden].
说白了,hidden就是每个方向,每个层的 隐藏单元的输出,所以是n_hidden个。
output的size(如果RNN设定的batch_first=True),那么就是[batch_size,seq_len,n_hidden],对于分类任务如果要取得最后一个output,只需添加下标 [ :,-1,:]
hn就是RNN的最后一个隐含状态,output就是RNN最终得到的结果。
代码
from torch import optim, nn
import numpy as np
import matplotlib.pyplot as plt
import torch
#参数设定
num_time_steps = 50
#训练时循环次数
input_size = 1
#输入维度
hidden_size = 16
#隐藏层节点个数
output_size = 1
#输出维度
#网络结构定义
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.rnn = nn.RNN(
input_size=input_size,
#输入数据的维度,比如使用one-hot编码单词,300个值表示一个字母维度就是300
hidden_size=hidden_size,
#隐藏层节点的个数
num_layers=1,#叠加的层数,此处只叠加一层
#即RNN经过几层堆叠得到结果
batch_first=True
#RNN默认输入是(seq_len, batch_size, input_size),此时batch_size在第一维度,所以需要设置成True
)
self.liner = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden_prev):
out, hidden_prev = self.rnn(x, hidden_prev)
out = out.view(-1, hidden_size)
# print(out.shape)
out = self.liner(out)
out = out.unsqueeze(dim=0)
return out, hidden_prev
#训练网络
model = Net()#初始化RNN
criterion = nn.MSELoss()#定义损失函数
optimizer = optim.Adam(model.parameters(), 1e-2)#优化器
hidden_prev = torch.zeros(1, 1, hidden_size) #初始化h0,即开始向后一层传递的记忆单元
for iter in range(6000):
start = np.random.randint(3, size=1)[0]#在0~3之间随机取开始的时刻点
#??
# print(start)
time_steps = np.linspace(start, start + 10, num_time_steps)
#在开始点和开始点+10之间均匀的取50个点,用于绘制图像,做数据集
data = np.sin(time_steps)
#计算数据预期值
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
#将数据转为Tensor类型:(batch_size,seq_len, input_size)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
output, hidden_prev = model(x, hidden_prev)
#output输出的是预测的49个值的结果,hp是隐藏层每个维度的输出值
# print('output',output.size())
# print('prev',hidden_prev.size())
hidden_prev = hidden_prev.detach()
#??分离出变量并且在新变量中不使用梯度
loss = criterion(output, y)
#计算误差值
model.zero_grad()
#梯度清零
loss.backward()
optimizer.step()
#反向传播优化
#没训练100次输出一次误差
if iter % 100 == 0:
print("Iter: {} loss: {} ".format(iter, loss))
#预测以及绘图
start = np.random.randint(3, size=1)[0]
print(start)
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
#将数据x转为Tensor类型
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
#将数据y转为Tensor类型
prediction = [] #预期数据矩阵
input = x[:, 0, :]
for _ in range(x.shape[1]):
input = input.view(1, 1, 1)
(pred, hidden_prev) = model(input, hidden_prev)
input = pred
prediction.append(pred.detach().numpy().ravel()[0])
x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(time_steps[:-1], x.ravel(), s=90)
plt.plot(time_steps[:-1], x.ravel())
plt.scatter(time_steps[1:], prediction)
plt.show()
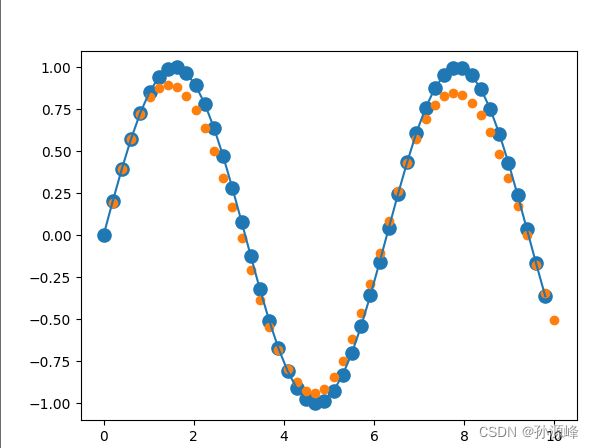
运行结果
总结
本周我们主要学习如何用RNN预测三角函数。下周我们将继续学习RNN的变形模型。