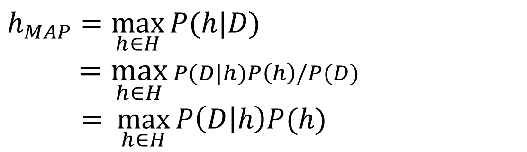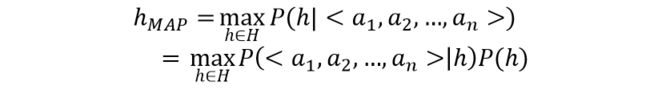朴素贝叶斯分类器
朴素贝叶斯分类器
- 1、分类概念
- 2、朴素贝叶斯分类
-
- 2.1 贝叶斯定理
- 2.2 极大后验假设
- 2.3 多维属性的联合概率
- 2.4 独立性假设
- 3、贝叶斯分类案例
- 4、连续数据如何求概率
- 5、朴素贝叶斯分类器的特点
- 6、贝叶斯算法实现鸢尾花分类
-
- 6.1 鸢尾花介绍
- 6.2 分类代码
1、分类概念
分类是找出描述和区分数据类或概念的模型,以便使用模型预测类标号未知的对象类标号。
分类一般分为两个阶段:
-
学习阶段:
- 建立描述预先定义的数据类或概念集的分类器。
- 训练集提供了每个训练元组的类标号,分类的学习过程也称为监督学习。
-
分类阶段:使用定义好的分类器进行分类的过程。
分类与预测是不同的概念,分类是预测分类(离散、无序)标号,而数值预测是建立连续值函数模型。分类与具类也是不同的概念,分类是有监督学习,提供了训练元组的类标号;聚类是无监督学习,不依赖有类标号的训练实例。
2、朴素贝叶斯分类
2.1 贝叶斯定理
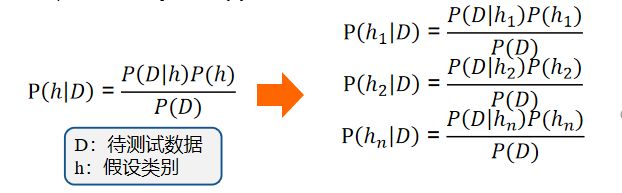
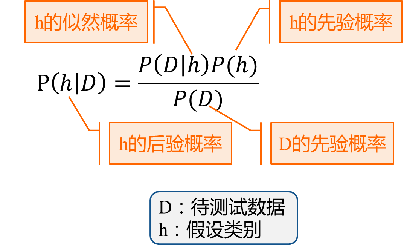
贝叶斯定理的公式为:
P ( h │ D ) = P ( D │ h ) P ( h ) P ( D ) P(ℎ│D)=\frac{P(D│ℎ)P(ℎ)}{P(D)} P(h│D)=P(D)P(D│h)P(h)
式中,D为待测试数据假设类别, P ( h ∣ D ) P(h|D) P(h∣D)是h的似然概率, P ( h ) P(h) P(h)是h的先验概率, P ( h ∣ D ) P(h|D) P(h∣D)是h的后验概率, P ( D ) P(D) P(D)是D的先验概率。
先看一个示例:一所学校里面有 60% 的男生(boy),40% 的女生(girl) 。男生总是穿长裤(pants),女生则一半穿长裤一半穿裙子。随机选取一个穿长裤的学生,他(她)是女生的概率是多大?
上述描述可形式化为:
已知P(Boy)=60%, P(Girl)=40%, P(Pants|Girl)=50%,P(Pants|Boy)=100% 求:P(Girl|Pants)
解答 :
P ( G i r l │ P a n t s ) = P ( G i r l ) P ( P a n t s │ G i r l ) P ( B o y ) P ( P a n t s ∣ B o y ) + P ( G i r l ) P ( P a n t s ∣ G i r l ) = P ( G i r l ) P ( P a n t s │ G i r l ) P ( P a n t s ) P(Girl│Pants)=\frac{P(Girl)P(Pants│Girl)}{P(Boy)P(Pants|Boy)+P(Girl)P(Pants|Girl)}=\frac{P(Girl)P(Pants│Girl)}{P(Pants)} P(Girl│Pants)=P(Boy)P(Pants∣Boy)+P(Girl)P(Pants∣Girl)P(Girl)P(Pants│Girl)=P(Pants)P(Girl)P(Pants│Girl)
直观理解:算出学校里面有多少穿长裤的,然后在这些人里面再算出有多少女生
对于上述问题能得到这样的观察知识: 一所学校里面有 60% 的男生(boy),40% 的女生(girl) 。男生总是穿长裤(pants),女生则一半穿长裤一半穿裙子。同样,我们不能直接观察到随机选取的一个穿长裤的学生,判断出该学生是男生还是女生。
对于不能直接观察到的部分,往往会提出假设。而对于不确定的事物,往往会有多个假设。
贝叶斯提供了一种计算假设后验概率 P ( h ∣ D ) P(h|D) P(h∣D)的方法,即后验概率与先验概率和似然概率乘积成正比。
2.2 极大后验假设
极大后验假设学习器在候选假设集合H中寻找给定数据D时可能性最大的假设h,h被称为极大后验假设(Maximum a posteriori: MAP)。确定MAP的方法是用贝叶斯公式计算每个候选假设的后验概率,计算式如下:
最后一步去掉了 P ( D ) P(D) P(D),因为它是不依赖于h的常量,或认为任何数据的先验概率相等。
2.3 多维属性的联合概率
已知:对象D是由多个属性组成的向量,那么结合上述极大后验假设,我们的目标可以写成:
但在这里遇到一个问题:计算 P ( < a 1 , a 2 , … , a n > │ h ) P(
2.4 独立性假设
之前提到的数据稀疏的问题可以用独立性假设来解决,也就是假设D的属性 a i a_i ai之间相互独立,那么上述公式可以写成:
P ( < a 1 , a 2 , … , a n > │ h ) = ∏ i P ( a i ∣ h ) \begin{aligned} P(
h M A P = max h ∈ H P ( h ∣ < a 1 , a 2 , … , a n > ) = max h ∈ H P ( < a 1 , a 2 , … , a n > │ h ) P ( h ) = max h ∈ H ∐ i P ( a i │ h ) P ( h ) \begin{aligned} ℎ_{MAP}&=\max_{h\in H}P (ℎ|
进行独立性假设之后,获得估计的 P ( a i │ h ) P(a_i│ℎ) P(ai│h)比 P ( < a 1 , a 2 , … , a n > │ h ) P(
3、贝叶斯分类案例
下面的训练集描述了购买电脑的情况统计。训练集的特征包括年龄、收入、爱好、信用以及购买情况。
| id | 年龄 | 收入 | 爱好 | 信用 | 购买 |
|---|---|---|---|---|---|
| 1 | 青 | 高 | 否 | 中 | 否 |
| 2 | 青 | 高 | 否 | 优 | 否 |
| 3 | 中 | 高 | 否 | 中 | 是 |
| 4 | 老 | 中 | 否 | 中 | 是 |
| 5 | 老 | 低 | 是 | 中 | 是 |
| 6 | 老 | 低 | 是 | 优 | 否 |
| 7 | 中 | 低 | 是 | 优 | 是 |
| 8 | 青 | 中 | 否 | 中 | 否 |
| 9 | 青 | 低 | 是 | 中 | 是 |
| 10 | 老 | 中 | 是 | 中 | 是 |
| 11 | 青 | 中 | 是 | 优 | 是 |
| 12 | 中 | 中 | 否 | 优 | 是 |
| 13 | 中 | 高 | 是 | 中 | 是 |
| 14 | 老 | 中 | 否 | 优 | 否 |
测试案例:一个收入中等、信用度良好的青年爱好游戏顾客,是否会购买电脑呢?
根据上表的训练集,可以得到如下已购买电脑的训练集。对于如下测试集,判断一个收入中等、信用度良好的青年爱好游戏的顾客是否会购买电脑。
| id | 年龄段 | 收入状况 | 爱好 | 信用度 | 购买电脑 |
|---|---|---|---|---|---|
| 3 | 中 | 高 | 否 | 中 | 是 |
| 4 | 老 | 中 | 否 | 中 | 是 |
| 5 | 老 | 低 | 是 | 中 | 是 |
| 7 | 中 | 低 | 是 | 优 | 是 |
| 9 | 青 | 低 | 是 | 中 | 是 |
| 10 | 老 | 中 | 是 | 中 | 是 |
| 11 | 青 | 中 | 是 | 优 | 是 |
| 12 | 中 | 中 | 否 | 优 | 是 |
| 13 | 中 | 高 | 是 | 中 | 是 |
首先计算测试集中购买电脑的客户中不同属性的概率:
P ( 青 年 ∣ 购 买 ) = 2 / 9 = 0.222 P ( 收 入 中 等 ∣ 购 买 ) = 4 / 9 = 0.444 P ( 爱 好 ∣ 购 买 ) = 6 / 9 = 0.667 P ( 信 用 中 ∣ 购 买 ) = 6 / 9 = 0.667 P(青年 |购买) = 2/9 = 0.222\\ P(收入中等 |购买) = 4/9 = 0.444\\ P(爱好 |购买) = 6/9 = 0.667\\ P(信用中 | 购买) =6/9 = 0.667 P(青年∣购买)=2/9=0.222P(收入中等∣购买)=4/9=0.444P(爱好∣购买)=6/9=0.667P(信用中∣购买)=6/9=0.667
然后根据如下公式,计算出购买电脑的似然概率:
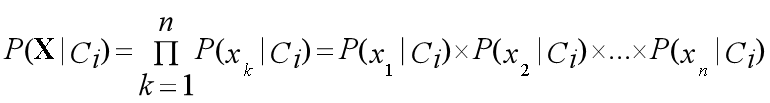
P ( X ∣ 购 买 ) = 0.222 × 0.444 × 0.667 × 0.667 = 0.044 P(X | 购买) = 0.222 ×0.444 ×0.667 ×0.667=0.044 P(X∣购买)=0.222×0.444×0.667×0.667=0.044
同样,我们可以得到不购买电脑的训练集。
| id | 年龄段 | 收入状况 | 爱好 | 信用度 | 购买电脑 |
|---|---|---|---|---|---|
| 1 | 青 | 高 | 否 | 中 | 否 |
| 2 | 青 | 高 | 否 | 优 | 否 |
| 6 | 老 | 低 | 是 | 优 | 否 |
| 8 | 青 | 中 | 否 | 中 | 否 |
| 14 | 老 | 中 | 否 | 优 | 否 |
那么测试集中不同属性下不购买电脑的概率:
P ( 青 年 ∣ 不 买 ) = 3 / 5 = 0.6 P ( 收 入 中 等 ∣ 不 买 ) = 2 / 5 = 0.4 P ( 爱 好 ∣ 不 买 ) = 1 / 5 = 0.2 P ( 信 用 中 ∣ 不 买 ) = 2 / 5 = 0.4 P(青年 |不买) = 3/5 = 0.6\\ P(收入中等 |不买) = 2/5 = 0.4\\ P(爱好 |不买) = 1/5 = 0.2\\ P(信用中 |不买) = 2/5 = 0.4 P(青年∣不买)=3/5=0.6P(收入中等∣不买)=2/5=0.4P(爱好∣不买)=1/5=0.2P(信用中∣不买)=2/5=0.4
同样,利用上面的公式计算出不购买电脑的似然概率:

P ( X ∣ 不 买 ) = 0.6 × 0.4 × 0.2 × 0.4 = 0.019 P(X |不买) =0.6 ×0.4 ×0.2 ×0.4=0.019 P(X∣不买)=0.6×0.4×0.2×0.4=0.019
用公式 P ( X ∣ C i ) P ( C i ) P(X|C_i)P(C_i) P(X∣Ci)P(Ci),可得:
P ( C 买 ) = 9 / 14 = 0.643 P ( C 不 买 ) = 5 / 14 = 0.357 P ( 购 买 ∣ X ) = 0.044 × 0.643 = 0.028 P ( 不 买 ∣ X ) = 0.019 × 0.357 = 0.007 P(C_买)=9/14=0.643\\ P(C_{不买})=5/14=0.357\\ P(购买|X) =0.044×0.643=0.028 \\ P(不买|X) = 0.019 ×0.357=0.007 P(C买)=9/14=0.643P(C不买)=5/14=0.357P(购买∣X)=0.044×0.643=0.028P(不买∣X)=0.019×0.357=0.007
4、连续数据如何求概率
下表描述的是不同收入情况下是否购买电脑的结果。那么,能否利用表格中的数据预测收入为121,无游戏爱好、信用良好的中年人是否会购买电脑呢?
| id | 收入 | 购买 |
|---|---|---|
| 1 | 125 | 否 |
| 2 | 100 | 否 |
| 3 | 70 | 否 |
| 4 | 120 | 否 |
| 5 | 95 | 是 |
| 6 | 60 | 否 |
| 7 | 220 | 否 |
| 8 | 85 | 是 |
| 9 | 75 | 否 |
| 10 | 90 | 是 |
这里的收入使用连续数据表示,因此不能采用之前的离散数据概率估计方法。对于连续数据,我们假设不同类别的收入分别服从不同的正态分布,利用参数估计两组正态分布期望和方差,就可以计算出收入为121时不购买电脑的概率,如下所示:
5、朴素贝叶斯分类器的特点
- 属性可以离散、也可以连续
- 数学基础坚实、分类效率稳定
- 对缺失和噪声数据不太敏感
- 属性如果不相关,分类效果很好
6、贝叶斯算法实现鸢尾花分类
6.1 鸢尾花介绍
鸢尾属(拉丁学名:Iris L.), 单子叶植物纲, 鸢尾科多年生草本植物, 开的花大而美丽, 观赏价值很高。 鸢尾属约300种, Iris数据集中包含了其中的三种: 山鸢尾(Setosa), 杂色鸢尾(Versicolour), 维吉尼亚鸢尾(Virginica), 每种50个数据, 共含150个数据。 在每个数据包含四个属性: 花萼长度,花萼宽度,花瓣长度,花瓣宽度, 可通过这四个属性预测鸢尾花卉属于 (山鸢尾, 杂色鸢尾, 维吉尼亚鸢尾) 哪一类。
数据集中部分数据如下图所示:
6.2 分类代码
import sklearn
# 导入高斯朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd
data_url = "Iris.csv"
df = pd.read_csv(data_url)
X = df.iloc[:,1:5]
y=df.iloc[:,5]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 使用高斯朴素贝叶斯进行计算
######## Begin ########
clf=GaussianNB()
######## End ########
clf.fit(X_train, y_train)
# 评估
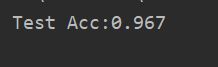
y_pred = clf.predict(X_test)
acc = np.sum(y_test == y_pred) / X_test.shape[0]
print("Test Acc:%.3f" % acc)