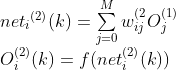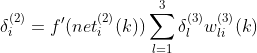BP神经网络整定PID

BP神经网络整定PID：

传统增量式数字PID控制算法为：

现引入三层BP神经网络，网络输入层为： j=1,2,...,M

隐含层的输入输出为：  i=1,2,...,Q

其中，为隐含层加权系数。隐含层是网络的内部信息处理层，负责信息变换。隐含层神经元的活化函数取正负对称的Sigmoid函数：

网络输出层的输入和输出为：

其中，表示神经网络输出层的三个输出节点，输出层向外界输出信息处理结果。这里的三个输出节点分别对应PID控制器的三个可调参数。而输出层神经元的活化函数为非负的Sigmoid函数：

性能指标函数为：

整个神经网络按E(k)对加权系数的负梯度方向搜索调整，修正网络的权系数，并附加一个使搜索调整快速收敛于全局极小的惯性项：

，式中为学习速率，为惯性系数。

其中y(k)为被控对象的传递函数。

且，由于未知，这里近似用符号函数取代，由此产生的计算不精确的影响通过调整学习速率来补偿。

推导出网络输出层权的学习算法为：

    l=1,2,3...

式中,

同理可得隐含层加权系数的学习算法：

  

  i=1,2,3...Q

式中,。

S函数：

function [sys,x0,str,ts,simStateCompliance] = sfun_BP(t,x,u,flag,T,j,xite,alfa)
switch flag,
  case 0,
    [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(T,j);
%初始化函数
  case 3,
    sys=mdlOutputs(t,x,u,xite,alfa);
%输出函数
  case {1,2,4,9},
    sys=[];
  otherwise
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(T,j)
%调用初始化函数，T步长，j隐含层神经元数
sizes = simsizes;
sizes.NumContStates  = 0;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 4;
%定义输出变量，包括控制变量u,三个PID参数：Kp,Ki,Kd
sizes.NumInputs      = 8;
%定义输入变量，包括7个参数[e(k);e(k-1);e(k-2);y(k);y(k-1);r(k);u(k-1)]和偏置量u(8)=1
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1; 
sys = simsizes(sizes);
x0  = [];
str = [];
ts  = [T 0];
global wi_2 wi_1 wo_2 wo_1
wi_2 =rand(j,4).*2-1;
%隐含层（k-2)权值系数矩阵，维数j*4，范围【-1，1】
wo_2 = rand(3,j);
%输出层（k-2）权值系数矩阵，维数3*j，范围【0，1】
wi_1 = wi_2;
%隐含层（k-1)权值系数矩阵，维数j*4
wo_1 = wo_2;
%输出层（k-1）权值系数矩阵，维数3*j
simStateCompliance = 'UnknownSimState';
function sys=mdlOutputs(t,x,u,xite,alfa)
%调用输出函数
M=[50;2;25];
%PID权值
global wi_2 wi_1 wo_2 wo_1
xi = [u(6),u(4),u(1),u(8)];
%神经网络的输入xi=[u(6),u(4),u(1),u(8)]=[r(k),y(k),e(k),1] 维数1*4
xx = [u(1)-u(2);u(1);u(1)+u(3)-2*u(2)];
%xx=[u(1)-u(2);u(1);u(1)+u(3)-2*u(2)]=[e(k)-e(k-1);e(k);e(k)+e(k-2)-2*e(k-1)]3*1
I = xi*wi_1';
%计算隐含层的输入，I=神经网络的输入*隐含层权值系数矩阵的转置wi_1'
Oh = (exp(I)-exp(-I))./(exp(I)+exp(-I));
%激活函数，计算隐含层的输出,为1*j的矩阵
O = wo_1*Oh';
%计算输出层的输入，维数3*1
K =exp(O)./(exp(O)+exp(-O));
%激活函数,计算输出层的输出K=[Kp,Ki,Kd]，维数为3*1
K(1)=M(1)*K(1);K(2)=M(2)*K(2);K(3)=M(3)*K(3);
uu = u(7)+K'*xx;
%根据增量式PID控制算法计算控制变量u(k) 维数1*1
if uu>15
    uu=15;
end
if uu<-15
    uu=-15;
end
%限制输出u
dyu = sign((u(4)-u(5))/(uu-u(7)+0.0001));
%计算输出层加权系数修正公式的sgn
%sign((y(k)-y(k-1))/(u(k)-u(k-1)+0.0001）)近似代表偏导 维数1*1
dO = 2./(exp(O)+exp(-O)).^2;
%激活函数，维数3*1
delta3 = u(1)*dyu*xx.*dO;
wo = wo_1+xite*delta3*Oh+alfa*(wo_1-wo_2);
%输出层加权系数矩阵的修正
dI = 2./(exp(I)+exp(-I)).^2;
%激活函数，维数1*j
wi = wi_1+xite*(dI.*(delta3'*wo))'*xi+alfa*(wi_1-wi_2);
%隐含层加权系数修正
wi_2=wi_1;
wi_1=wi;
wo_2=wo_1;
wo_1=wo;
sys = [uu;K(:)];
%输出层输出sys=[uu;Kp;Ki;Kd]

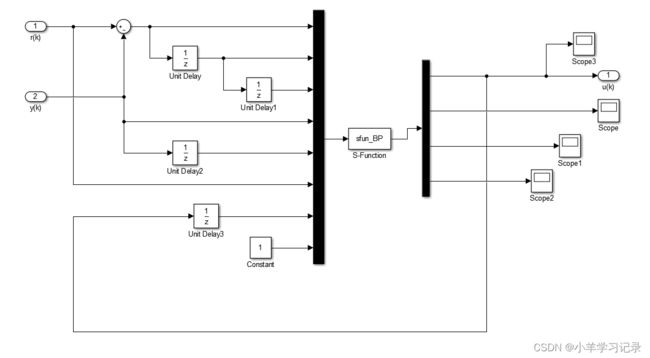
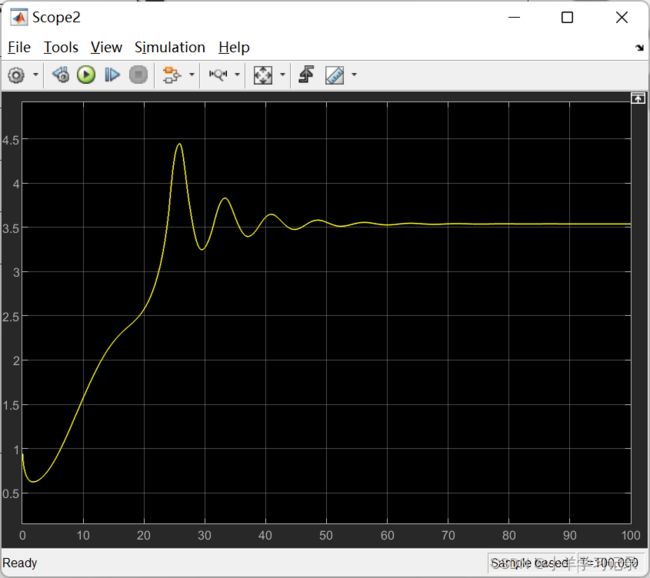
simulink：

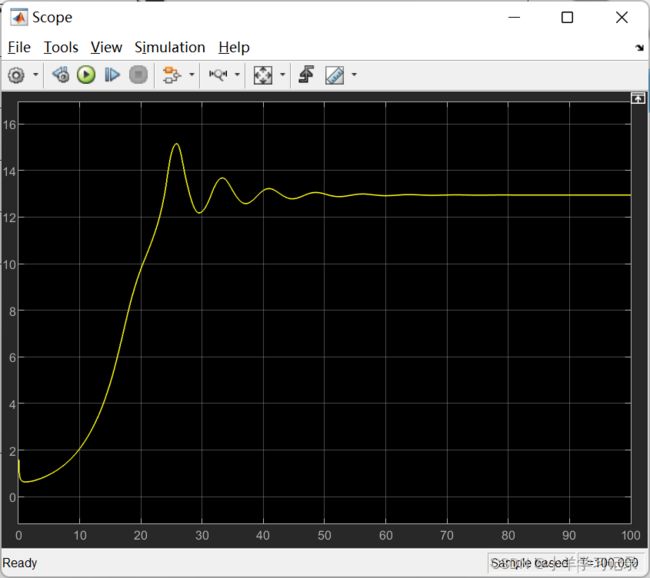
得到的阶跃响应为：

其中，

KP:

KI:

KD:

参考原文链接：https://blog.csdn.net/weixin_42650162/article/details/90678503

参考文献

[1]李捷菲. 基于BP神经网络的PID控制系统研究与设计[D].吉林大学,2019.

[2]K. Jiangming and L. Jinhao, "Self-Tuning PID Controller Based on Improved BP Neural Network," 2009 Second International Conference on Intelligent Computation Technology and Automation, 2009, pp. 95-98, doi: 10.1109/ICICTA.2009.32.

[3]Gan Jialiang, Li Zhimin and Tan Huaijiang, "Research on self-tuning PID control strategy based on BP neural network," Proceedings of 2011 International Conference on Electronics and Optoelectronics, 2011, pp. V2-16-V2-21, doi: 10.1109/ICEOE.2011.6013163.