day7-Stacking与案例（幸福感预测）

day7-Stacking与案例（幸福感预测）

---

心得体会

开源学习组织datawhale的组队学习第七天，学习了集成学习方法的最后一个成员–Stacking，我们可以对三个GBDT模型进行Stacking融合，那么每个GBDT模型都可以看做一个基模型，这样的话，这三个GBDT模型可以标识为mode1、mode2、mode3，利用五折的方法，能够获取每个基模型对每个样本的预测结果，次学习器学的就是 把这些预测结果作为新的次学习器的特征进行学习组织出最优的融合结果。 由模型做融合而不是简单的加权融合就是stacking最核心的思想。第一次实践了集成学习案例-幸福感预测，进行了数据预处理、模型增广、特征工程等操作，并套用集成学习的模型进行建模，得到预测结果。在这里感谢datawhale开源社区的小伙伴们给予的学习帮助，今后的学习也要一样加油呀

---

提示：以下是本篇文章正文内容，下面案例以及设计到的知识点均为datawhale开源组织提供

Stacking流程：

前言

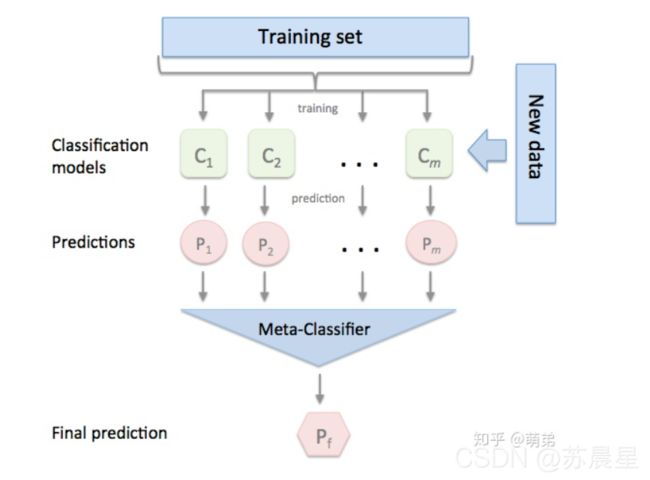
在前几个章节中，我们学习了关于回归和分类的算法，同时也讨论了如何将这些方法集成为强大的算法的集成学习方式，分别是Bagging和Boosting。本章我们继续讨论集成学习方法的最后一个成员–Stacking，这个集成方法在比赛中被称为“懒人”算法，因为它不需要花费过多时间的调参就可以得到一个效果不错的算法，同时，这种算法也比前两种算法容易理解的多，因为这种集成学习的方式不需要理解太多的理论，只需要在实际中加以运用即可。 stacking严格来说并不是一种算法，而是精美而又复杂的，对模型集成的一种策略。Stacking集成算法可以理解为一个两层的集成，第一层含有多个基础分类器，把预测的结果(元特征)提供给第二层， 而第二层的分类器通常是逻辑回归，他把一层分类器的结果当做特征做拟合输出预测结果。在介绍Stacking之前，我们先来对简化版的Stacking进行讨论，也叫做Blending，接着我们对Stacking进行更深入的讨论。

一、Blending集成学习算法

1、算法原理

(1) 将数据划分为训练集和测试集(test_set)，其中训练集需要再次划分为训练集(train_set)和验证集(val_set)；
(2) 创建第一层的多个模型，这些模型可以使同质的也可以是异质的；
(3) 使用train_set训练步骤2中的多个模型，然后用训练好的模型预测val_set和test_set得到val_predict, test_predict1；
(4) 创建第二层的模型,使用val_predict作为训练集训练第二层的模型；
(5) 使用第二层训练好的模型对第二层测试集test_predict1进行预测，该结果为整个测试集的结果。

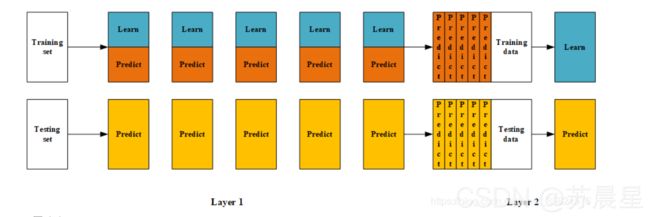
在(1)步中，总的数据集被分成训练集和测试集，如80%训练集和20%测试集，然后在这80%的训练集中再拆分训练集70%和验证集30%，因此拆分后的数据集由三部分组成：训练集80%* 70%
、测试集20%、验证集80%* 30% 。训练集是为了训练模型，测试集是为了调整模型(调参)，测试集则是为了检验模型的优度。
在(2)-(3)步中，我们使用训练集创建了K个模型，如SVM、random forests、XGBoost等，这个是第一层的模型。 训练好模型后将验证集输入模型进行预测，得到K组不同的输出，我们记作A 1 , . . . , A K ，然后将测试集输入K个模型也得到K组输出，我们记作B 1 , . . . , B K ，其中A i 的样本数与验证集一致，B i 的样本数与测试集一致。如果总的样本数有10000个样本，那么使用5600个样本训练了K个模型，输入验证集2400个样本得到K组2400个样本的结果A 1 , . . . , A K，输入测试集2000个得到K组2000个样本的结果B 1 , . . . , B K 。
在(4)步中，我们使用K组2400个样本的验证集结果A 1 , . . . , A K 作为第二层分类器的特征，验证集的2400个标签为因变量，训练第二层分类器，得到2400个样本的输出。
在(5)步中，将输入测试集2000个得到K组2000个样本的结果B 1 , . . . , B K 放入第二层分类器，得到2000个测试集的预测结果。

以上是Blending集成方式的过程，接下来我们来分析这个集成方式的优劣：
其中一个最重要的优点就是实现简单粗暴，没有太多的理论的分析。但是这个方法的缺点也是显然的：blending只使用了一部分数据集作为留出集进行验证，也就是只能用上数据中的一部分，实际上这对数据来说是很奢侈浪费的。
关于这个缺点，我们以后再做改进，我们先来用一些案例来使用这个集成方式。

2、相关案例

# 加载相关工具包
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
plt.style.use("ggplot")
%matplotlib inline
import seaborn as sns

# 创建数据
from sklearn import datasets 
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
data, target = make_blobs(n_samples=10000, centers=2, random_state=1, cluster_std=1.0 )
## 创建训练集和测试集
X_train1,X_test,y_train1,y_test = train_test_split(data, target, test_size=0.2, random_state=1)
## 创建训练集和验证集
X_train,X_val,y_train,y_val = train_test_split(X_train1, y_train1, test_size=0.3, random_state=1)
print("The shape of training X:",X_train.shape)
print("The shape of training y:",y_train.shape)
print("The shape of test X:",X_test.shape)
print("The shape of test y:",y_test.shape)
print("The shape of validation X:",X_val.shape)
print("The shape of validation y:",y_val.shape)

#  设置第一层分类器
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier

clfs = [SVC(probability = True),RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),KNeighborsClassifier()]

# 设置第二层分类器
from sklearn.linear_model import LinearRegression
lr = LinearRegression()

# 输出第一层的验证集结果与测试集结果
val_features = np.zeros((X_val.shape[0],len(clfs)))  # 初始化验证集结果
test_features = np.zeros((X_test.shape[0],len(clfs)))  # 初始化测试集结果

for i,clf in enumerate(clfs):
    clf.fit(X_train,y_train)
    val_feature = clf.predict_proba(X_val)[:, 1]
    test_feature = clf.predict_proba(X_test)[:,1]
    val_features[:,i] = val_feature
    test_features[:,i] = test_feature

 print(val_feature)
 # 得到
 array([[2.03768927e-04, 0.00000000e+00, 0.00000000e+00],
       [5.14759728e-04, 0.00000000e+00, 0.00000000e+00],
       [9.99999841e-01, 1.00000000e+00, 1.00000000e+00],
       ...,
       [9.99999888e-01, 1.00000000e+00, 1.00000000e+00],
       [9.99999390e-01, 1.00000000e+00, 1.00000000e+00],
       [9.99999861e-01, 1.00000000e+00, 1.00000000e+00]])

# 将第一层的验证集的结果输入第二层训练第二层分类器
lr.fit(val_features,y_val)
# 输出预测的结果
from sklearn.model_selection import cross_val_score
cross_val_score(lr,test_features,y_test,cv=5)

可以看到，在每一折的交叉验证的效果都是非常好的，这个集成学习方法在这个数据集上是十分有效的，不过这个数据集是我们虚拟的，因此大家可以把他用在实际数据上看看效果。

二、Stacking集成学习算法

基于前面对Blending集成学习算法的讨论，我们知道：Blending在集成的过程中只会用到验证集的数据，对数据实际上是一个很大的浪费。为了解决这个问题，我们详细分析下Blending到底哪里出现问题并如何改进。在Blending中，我们产生验证集的方式是使用分割的方式，产生一组训练集和一组验证集，这让我们联想到交叉验证的方式。顺着这个思路，我们对Stacking进行建模(如下图)：

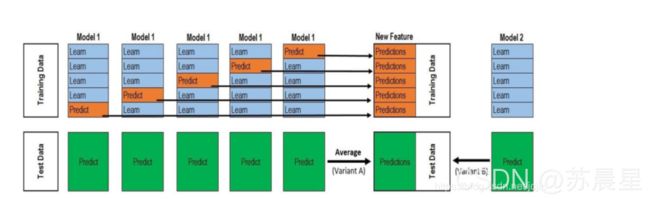
首先将所有数据集生成测试集和训练集（假如训练集为10000,测试集为2500行），那么上层会进行5折交叉检验，使用训练集中的8000条作为训练集，剩余2000行作为验证集（橙色）。
每次验证相当于使用了蓝色的8000条数据训练出一个模型，使用模型对验证集进行验证得到2000条数据，并对测试集进行预测，得到2500条数据，这样经过5次交叉检验，可以得到中间的橙色的5* 2000条验证集的结果(相当于每条数据的预测结果)，5* 2500条测试集的预测结果。
接下来会将验证集的5* 2000条预测结果拼接成10000行长的矩阵，标记为A 1，而对于5* 2500行的测试集的预测结果进行加权平均，得到一个2500一列的矩阵，标记为B 1 。上面得到一个基模型在数据集上的预测结果A 1、B 1 ,这样当我们对3个基模型进行集成的话，相于得到了A 1 、A 2 、A 3 ​ 、B 1、B 2 、B 3 六个矩阵。之后我们会将A 1 、A 2 、A 3 并列在一起成10000行3列的矩阵作为training data,B 1 、B 2 、B 3 合并在一起成2500行3列的矩阵作为testing data，让下层学习器基于这样的数据进行再训练。
再训练是基于每个基础模型的预测结果作为特征（三个特征），次学习器会学习训练如果往这样的基学习的预测结果上赋予权重w，来使得最后的预测最为准确。
下面，我们来实际应用下Stacking是如何集成算法的

由于sklearn并没有直接对Stacking的方法，因此我们需要下载mlxtend工具包(pip install mlxtend)

# 1. 简单堆叠3折CV分类
from sklearn import datasets

iris = datasets.load_iris()
X,y = iris.data[:,1:3],iris.target
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier

import matplotlib.pyplot as plt
plt.style.use("ggplot")
%matplotlib inline

RANDOM_SEED = 42

clf1 = KNeighborsClassifier(n_neighbors = 1)
clf2 = RandomForestClassifier(random_state = RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1,clf2,clf3],
                            meta_classifier=lr,
                            random_state=RANDOM_SEED)

print('3-fold cross validation: \n')  # 输出3折验证集的结果

for clf,label in zip([clf1,clf2,clf3,sclf],['KNN','Random Forest','Naive Bayes','StackingClassifier']):
    scores = cross_val_score(clf,X,y,cv = 3,scoring = 'accuracy')
    print('Accuraacy: %0.2f (+/- %0.2f) [%s]' % (scores.mean(),scores.std(),label))

3-fold cross validation: 

Accuraacy: 0.91 (+/- 0.01) [KNN]
Accuraacy: 0.95 (+/- 0.01) [Random Forest]
Accuraacy: 0.91 (+/- 0.02) [Naive Bayes]
Accuraacy: 0.93 (+/- 0.02) [StackingClassifier]

clf

StackingCVClassifier(classifiers=[KNeighborsClassifier(n_neighbors=1),
                                  RandomForestClassifier(random_state=42),
                                  GaussianNB()],
                     meta_classifier=LogisticRegression(), random_state=42)

# 我们画出决策边界
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
import itertools

gs = gridspec.GridSpec(2,2)
fig = plt.figure(figsize=(10,8))
for clf,lab,grd in zip([clf1,clf2,clf3,sclf],
                       ['KNN',
                        'Random Forest',
                        'Naive Bayes',
                        'StackingCVClassifer'],
                        itertools.product([0,1],repeat=2)):
    clf.fit(X,y)
    ax = plt.subplot(gs[grd[0],grd[1]])
    fig = plot_decision_regions(X=X,y=y,clf=clf)  # 绘制决策区域!
    plt.title(lab)
plt.show()

使用第一层所有基分类器所产生的类别概率值作为meta-classfier的输入。需要在StackingClassifier 中增加一个参数设置：use_probas = True。

另外，还有一个参数设置average_probas = True,那么这些基分类器所产出的概率值将按照列被平均，否则会拼接。

例如：

基分类器1：predictions=[0.2,0.2,0.7]

基分类器2：predictions=[0.4,0.3,0.8]

基分类器3：predictions=[0.1,0.4,0.6]

1）若use_probas = True，average_probas = True，

则产生的meta-feature 为：[0.233, 0.3, 0.7]

2）若use_probas = True，average_probas = False，

则产生的meta-feature 为：[0.2,0.2,0.7,0.4,0.3,0.8,0.1,0.4,0.6]

# 2.使用概率作为元特征
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
                            use_probas=True,  # 
                            meta_classifier=lr,
                            random_state=42)

print('3-fold cross validation:\n')

for clf, label in zip([clf1, clf2, clf3, sclf], 
                      ['KNN', 
                       'Random Forest', 
                       'Naive Bayes',
                       'StackingClassifier']):

    scores = cross_val_score(clf, X, y, 
                                              cv=3, scoring='accuracy')
    print("Accuracy: %0.2f (+/- %0.2f) [%s]" 
          % (scores.mean(), scores.std(), label))

3-fold cross validation:

Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.95 (+/- 0.02) [StackingClassifier]

# 3 堆叠5折CV分类与网格搜索(结合网格搜索调参优化)
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB 
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from mlxtend.classifier import StackingCVClassifier
# Initializing models 模型初始化

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3], 
                            meta_classifier=lr,
                            random_state=42)

params = StackingCVClassifier(classifiers = [clf1,clf2,clf3],
                              meta_classifier = lr,
                              random_state = 42)

params = {'kneighborsclassifier__n_neighbors': [1, 5],
          'randomforestclassifier__n_estimators': [10, 50],
          'meta_classifier__C': [0.1, 10.0]}

grid = GridSearchCV(estimator=sclf, 
                    param_grid=params, 
                    cv=5,
                    refit=True)
grid.fit(X,y)

cv_keys = ('mean_test_score','std_test_score','params')

for r, _ in enumerate(grid.cv_results_['mean_test_score']):
    print("%0.3f +/- %0.2f %r"
          % (grid.cv_results_[cv_keys[0]][r],
             grid.cv_results_[cv_keys[1]][r] / 2.0,
             grid.cv_results_[cv_keys[2]][r]))  # 

print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)

0.947 +/- 0.03 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.933 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.940 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.940 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Best parameters: {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
Accuracy: 0.95

grid.cv_results_[cv_keys[0]]

array([0.94666667, 0.93333333, 0.94      , 0.94      , 0.95333333,
       0.95333333, 0.95333333, 0.95333333])

# 4.在不同特征子集上运行的分类器的堆叠
##不同的1级分类器可以适合训练数据集中的不同特征子集。以下示例说明了如何使用scikit-learn管道和ColumnSelector：
from sklearn.datasets import load_iris
from mlxtend.classifier import StackingCVClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression

iris = load_iris()
X = iris.data
y = iris.target

pipe1 = make_pipeline(ColumnSelector(cols=(0, 2)),  # 选择第0,2列
                      LogisticRegression())
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)),  # 选择第1,2,3列
                      LogisticRegression())

sclf = StackingCVClassifier(classifiers=[pipe1, pipe2], 
                            meta_classifier=LogisticRegression(),
                            random_state=42)

sclf.fit(X, y)

# 5.ROC曲线 decision_function
### 像其他scikit-learn分类器一样，它StackingCVClassifier具有decision_function可用于绘制ROC曲线的方法。
### 请注意，decision_function期望并要求元分类器实现decision_function。
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier

iris = datasets.load_iris()
X, y = iris.data[:, [0, 1]], iris.target

# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]

RANDOM_SEED = 42

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=RANDOM_SEED)

clf1 =  LogisticRegression()
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = SVC(random_state=RANDOM_SEED)
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
                            meta_classifier=lr)

# Learn to predict each class against the other
classifier = OneVsRestClassifier(sclf)
y_score = classifier.fit(X_train, y_train).decision_function(X_test)

# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

plt.figure()
lw = 2
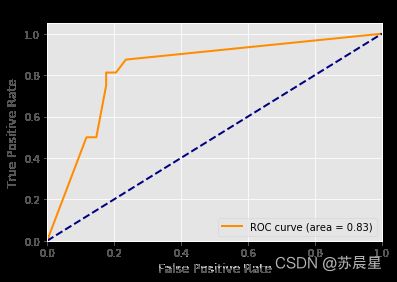
plt.plot(fpr[2], tpr[2], color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

三、案例一（幸福感预测）

思路理解

准备工作：首先进行数据分析，将几张数据表对应的信息内容加以对比，理解数据讲述的内容；导入各种包；导入数据集，可选用‘latin-1’的编码方式（向下兼容多），删去一些统计错误的数据（按行删除），删去‘happiness’目标列，合并训练集与测试集；查看数据的基本信息。

数据预处理：填补缺失值，利用所给的数据集信息查看变量对应的意思，根据常识对缺失值做出相应判断（主观想法）进行填充，其他缺失值用正常数据的平均值或者众数等合理值填充；对特殊格式的数据进行处理，将数据与数据联系起来（例如：用调查时间的年份减去出生年份得到年龄，进行年龄分层，将连续值转换为离散值）；对错误值进行处理，参考所给数据集对数据进行合理性判断；

数据增广：进一步分析特征之间的关系，添加新特征（例如：收入比、悠闲指数）。这里将原来131维的特征扩充到了272维。然后删去数值特别少和之前使用过的特征，最后得到263个特征。

特征工程：构建完成三组特征工程。第一组即为刚刚构建的原始数据集；第二组为用LightGBM选出263个特征中最重要的49个特征，计算每个特征的重要性，并做重要性排序，选择图像跳变前的49个最重要特征；第三组为对有需要的离散型变量进行one-hot编码后合成的数据集，共383维。

金字塔型建模：利用lightgbm、xgboost等多种模型对原始263维数据进行建模，得到预测结果，然后对得到的结果进行模型融合集成学习（stacking），得到融合后的预测结果；如法炮制对最重要的49维数据集、one-hot编码后的383维数据集进行处理，得到两者的预测结果；最后对三种维度数据集的预测结果进行模型融合，得到最终结果（整个过程其实就是套娃，举个例子：假设我有三组数据A、B、C，然后A组数据用4个模型去跑，得到A1、A2、A3、A4的预测结果，将四组预测结果模型融合得到AS预测结果，同理对B、C组数据进行处理，得到BS、CS预测结果，最后，将AS、BS、CS三组结果进行融合，得到最终结果S）

模型保存：最后保存为csv等格式，这里我们预测出的值为1-5的连续值，但是我们的ground truth是整数值，所以为了进一步优化我们的结果，我们对结果进行整数解的近似处理。（例如：值大于1.96，小于2.04的直接置为整数2）

详细过程请见下篇文章
day07-幸福感预测详解：
https://blog.csdn.net/wangzhouf/article/details/119972485

总结

Blending与Stacking对比：
Blending的优点在于：

• 比stacking简单（因为不用进行k次的交叉验证来获得stacker feature）

而缺点在于：

• 使用了很少的数据（是划分hold-out作为测试集，并非cv）
• blender可能会过拟合（其实大概率是第一点导致的）
• stacking使用多次的CV会比较稳健

相关资料：
【1】教案：https://github.com/datawhalechina/ensemble-learning
【2】datawhale开源学习社区：http://datawhale.club/