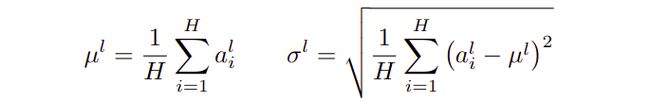(十一)数据归一化方法BN/LN/GN/IN

---

欢迎访问个人网络日志知行空间

---

0. Introduction

在神经网络的训练过程中，网络的收敛情况非常依赖于参数的初始化情况，使用Normalization的方法可以增强模型训练过程中的鲁棒性。目前常用的Normalization方法有Batch Normalization、Layer Normalization、Group Normalization、Instance Normalization四种方法，具体分别是指在一个batch的数据上分别在不同维度上做Normalization。如下图：

图中N表示一个Batch的大小，WH表示特征图宽高方向resize到一起后的维度方向，C表示不同的特征通道，G表示在通道方向做Group Normalization时每组包含的通道数的大小。

1.Batch Normalization

Batch Normalization是谷歌的Sergey Ioffe等于2015年03月份提交的论文Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift中提出的。

其中$x_i$是维度为$C$的数据，分别求每个维度在$batch$方向的均值和方差，然后进行归一化。值得注意的是方程

$$y_i\leftarrow \gamma \widehat{x_i}+\beta$$

相当于对归一化后的数据做了线性变换，这里$\gamma$和$\beta$都是在网络训练过程中需要学习的参数。根据上述BN的计算方式可求得反向传播的链路图：

由此使用Batch Normalization Layer时，其对应的反向和前向推理代码为，参考自CS231N homework2：

## Forward
def batchnorm_forward(x, gamma, beta, bn_param):
    """Forward pass for batch normalization.

    During training the sample mean and (uncorrected) sample variance are
    computed from minibatch statistics and used to normalize the incoming data.
    During training we also keep an exponentially decaying running mean of the
    mean and variance of each feature, and these averages are used to normalize
    data at test-time.

    At each timestep we update the running averages for mean and variance using
    an exponential decay based on the momentum parameter:

    running_mean = momentum * running_mean + (1 - momentum) * sample_mean
    running_var = momentum * running_var + (1 - momentum) * sample_var

    Note that the batch normalization paper suggests a different test-time
    behavior: they compute sample mean and variance for each feature using a
    large number of training images rather than using a running average. For
    this implementation we have chosen to use running averages instead since
    they do not require an additional estimation step; the torch7
    implementation of batch normalization also uses running averages.

    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - bn_param: Dictionary with the following keys:
      - mode: 'train' or 'test'; required
      - eps: Constant for numeric stability
      - momentum: Constant for running mean / variance.
      - running_mean: Array of shape (D,) giving running mean of features
      - running_var Array of shape (D,) giving running variance of features

    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """
    mode = bn_param["mode"]
    eps = bn_param.get("eps", 1e-5)
    momentum = bn_param.get("momentum", 0.9)

    N, D = x.shape
    running_mean = bn_param.get("running_mean", np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get("running_var", np.zeros(D, dtype=x.dtype))

    out, cache = None, None
    if mode == "train":

        avg = x.mean(axis=0)
        var = x.var(axis=0)
        std = np.sqrt(var)
        x_hat = avg / (std + eps)
        out = x_hat * gamma + beta
        
        shape = bn_param.get("shape", (N, D))
        axis = bn_param.get("axis", 0)
        cache = x, avg, var, std, gamma, x_hat, beta, shape, axis

        if axis == 0:
          running_mean = running_mean * momentum + (1 - momentum) * avg
          running_var = running_var * momentum + (1 - momentum) * var
    elif mode == "test":

        x_hat = (x - running_mean) / (np.sqrt(running_var) + eps)
        out = x_hat * gamma + beta

    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    # Store the updated running means back into bn_param
    bn_param["running_mean"] = running_mean
    bn_param["running_var"] = running_var

    return out, cache

## Backward
def batchnorm_backward_alt(dout, cache):
    """Alternative backward pass for batch normalization.

    For this implementation you should work out the derivatives for the batch
    normalizaton backward pass on paper and simplify as much as possible. You
    should be able to derive a simple expression for the backward pass.
    See the jupyter notebook for more hints.

    Note: This implementation should expect to receive the same cache variable
    as batchnorm_backward, but might not use all of the values in the cache.

    Inputs / outputs: Same as batchnorm_backward
    """
    dx, dgamma, dbeta = None, None, None
    _, _, _, std, gamma, x_hat, _, shape, axis = cache # expand cache
    S = lambda x: x.sum(axis=0)                     # helper function
    
    dbeta = dout.reshape(shape, order='F').sum(axis)            # derivative w.r.t. beta
    dgamma = (dout * x_hat).reshape(shape, order='F').sum(axis) # derivative w.r.t. gamma
    
    dx = dout * gamma / (len(dout) * std)          # temporarily initialize scale value
    dx = len(dout)*dx  - S(dx*x_hat)*x_hat - S(dx) # derivative w.r.t. unnormalized x

    return dx, dgamma, dbeta

在以上代码中，BatchNorm层在训练结束推理时使用的是训练时得到的running average和running variance，在反向传播梯度时是根据链式法则求出BN层整体的梯度公式来计算梯度，可以减少中间变量的存储和计算，减少运算量和内存占用。

3.Layer Normalization

Batch Normalization在使用过程中依赖batch size的大小，当模型比较复杂，占用内存过多时很难使用大的batch size进行网络训练，这时BN的效果会受到限制，2016年Hinton等提出的LayerNormalization克服了这些问题，可以作为batch size 较小时Batch Normalization的一种替代方案。

其中，$H$表示当前层隐层单元的数量，当使用的是卷积神经网络时，Layer Normalization是作用在卷积核作用在输入上得到的输出的每个通道上，输出的每个通道算做一层，在该层上做Normalization。

代码实现：

def layernorm_forward(x, gamma, beta, ln_param):
    """Forward pass for layer normalization.
    During both training and test-time, the incoming data is normalized per data-point,
    before being scaled by gamma and beta parameters identical to that of batch normalization.
    Note that in contrast to batch normalization, the behavior during train and test-time for
    layer normalization are identical, and we do not need to keep track of running averages
    of any sort.
    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - ln_param: Dictionary with the following keys:
        - eps: Constant for numeric stability
    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """
    out, cache = None, None
    eps = ln_param.get("eps", 1e-5)
    ln_param.setdefault('mode', 'train')       # same as batchnorm in train mode
    ln_param.setdefault('axis', 1)             # over which axis to sum for grad
    [gamma, beta] = np.atleast_2d(gamma, beta) # assure 2D to perform transpose

    out, cache = batchnorm_forward(x.T, gamma.T, beta.T, ln_param) # same as batchnorm
    out = out.T                                                    # transpose back
    return out, cache


def layernorm_backward(dout, cache):
    """Backward pass for layer normalization.
    For this implementation, you can heavily rely on the work you've done already
    for batch normalization.
    Inputs:
    - dout: Upstream derivatives, of shape (N, D)
    - cache: Variable of intermediates from layernorm_forward.
    Returns a tuple of:
    - dx: Gradient with respect to inputs x, of shape (N, D)
    - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
    - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
    """
    dx, dgamma, dbeta = None, None, None
    dx, dgamma, dbeta = batchnorm_backward_alt(dout.T, cache) # same as batchnorm backprop
    dx = dx.T # transpose back dx
    return dx, dgamma, dbeta

从上面代码可以看到，Layer Normalization是在每个样本的每层输出上实现的，因此可以复用Batch Normalization的实现。

4.Group Normalization

Group Normalization是2018年06月份HeKaiMing等提出的论文中发表的方法，作为Batch Normalization的另一种替代。

## pytorch example
import torch
x = torch.randn(1, 4, 2, 2)
m = torch.nn.GroupNorm(2, 4)
output = m(x)
print(output)

# equal to 
gx1 = x[:, :2, :, :]
gx2 = x[:, 2:, :, :]
mu1 = torch.mean(gx1)
mu2 = torch.mean(gx2)
std1 = torch.sqrt(torch.var(gx1))
std2 = torch.sqrt(torch.var(gx2))
x[:, :2, :, :] = (x[:, :2, :, :] - mu1) / (std1  + 1e-05)
x[:, 2:, :, :] = (x[:, 2:, :, :] - mu2) / (std2 + 1e-05)
print(x)

6.Instance Normalization

Instance Normalization 是2017年1月份Dmitry Ulyanov等发表的论文Improved Texture Networks: Maximizing Quality and Diversity in Feed-forward Stylization and Texture Synthesis中的提出的方法，其作用在单个样本的一个通道上，相当于num_groups=1的Group Normalization。

---

欢迎访问个人网络日志知行空间

---

参考资料

• 1.https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html
• 2.https://github.com/mantasu/cs231n/blob/master/assignment2/cs231n/layers.py
• 3.Group Normalization in Pytorch (With Examples)
• 4.GROUPNORM