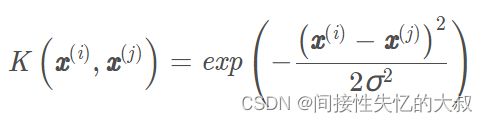R语言-聚类、分类、逻辑回归、决策树、推断树，支持向量机

聚类分析

1. 聚类的定义

聚类分析是根据在数据中发现的描述对象及其关系的信息，将数据对象分组。是一种归约技术，旨在揭露一个数据集中观测的子集。它可以把大量的观测值归约为若干个类。组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。组内相似性越大，组间差距越大，说明聚类效果越好。

图1-1 聚类分析示意图

最常用的两种聚类方法是层次聚类和划分聚类。

1.1层次聚类

1.1.1层次聚类定义与特点

基于层次的聚类方法是指对给定的数据进行层次分解，直到满足某种条件为止。该算法根据层次分解的顺序分为自底向上法和自顶向下法，即凝聚式层次聚类算法和分裂式层次聚类算法。

（1）自底向上法

首先，每个数据对象都是一个簇，计算数据对象之间的距离，每次将距离最近的点合并到同一个簇。然后，计算簇与簇之间的距离，将距离最近的簇合并为一个大簇。不停地合并，直到合成了一个簇，或者达到某个终止条件为止。簇与簇的距离的计算方法有最短距离法、中间距离法、类平均法等，其中，最短距离法是将簇与簇的距离定义为簇与簇之间数据对象的最短距离。自底向上法的代表算法是AGNES(AGglomerativeNESing)算法。

（2）自顶向下法

该方法在一开始所有个体都属于一个簇，然后逐渐细分为更小的簇，直到最终每个数据对象都在不同的簇中，或者达到某个终止条件为止。自顶向下法的代表算法是 DIANA（DivisiveANAlysis）算法。

基于层次的聚类算法的主要优点包括，距离和规则的相似度容易定义，限制少，不需要预先制定簇的个数，可以发现簇的层次关系。基于层次的聚类算法的主要缺点包括，计算复杂度太高，奇异值也能产生很大影响，算法很可能聚类成链状。

1.1.2层次聚类算法

对与层次聚类来说，最常用的算法是单联动、全联动、平均联动、质心和ward方法。

层次聚类方法
单联动	一个类中的点和另一个类中点的最小距离
全联动	一个类中的点和另一个类中点的最大距离
平均联动	一个类中的点和另一个类中点的平均距离
质心	两类中质心之间的距离。对单个变量来说，质心就是变量的值
Ward法	两个类之间的所有变量的方差分析的平方和

1.1.3层次聚类分析

首先载入数据，在这里使用平均联动聚类方法处理营养数据，目的是基于27种食物的营养信息辨别其相似性、相异性并分组。

data(nutrient, package="flexclust")

row.names(nutrient) <- tolower(row.names(nutrient))

nutrient.scaled <- scale(nutrient)                                  

d <- dist(nutrient.scaled)                                          

fit.average <- hclust(d, method="average")                          

plot(fit.average, hang=-1, cex=.8, main="Average Linkage Clustering")

 

图1-2 营养数据的平均联动

如果最终目标是这些食品分配到的类较少，因此需要额外的分析来选择聚类的适当个数。Nbclust()函数的输入包括需要做聚类的矩阵或是数据框，使用的距离测度和聚类方法，并考虑最小和最大聚类的个数来进行聚类。他返回每一个聚类指数，同时输出建议聚类的最佳数目。下面为该方法处理营养数据的平均联动聚类。

代码如下：

library(NbClust)

nc <- NbClust(nutrient.scaled, distance="euclidean",

              min.nc=2, max.nc=15, method="average")

par(opar)

table(nc$Best.n[1,])

barplot(table(nc$Best.n[1,]),

        xlab="Numer of Clusters", ylab="Number of Criteria",

        main="Number of Clusters Chosen by 26 Criteria")

 

图1-3 推荐聚类个数

通过分析上图，可以通过“投票”最多的聚类个数，并选择其中一个使的解释最有意义，下面的代码清单展示了五类聚类的方案。

clusters <- cutree(fit.average, k=5)

table(clusters)

aggregate(nutrient, by=list(cluster=clusters), median)

aggregate(as.data.frame(nutrient.scaled), by=list(cluster=clusters),

          median)

plot(fit.average, hang=-1, cex=.8,  

     main="Average Linkage Clustering\n5 Cluster Solution")

rect.hclust(fit.average, k=5)

cutree()函数用来把树状图分成五类，结果有原始度量和标准度量两种形式，树状图被重新绘制，rect.hclust()函数用来叠加五类的解决方案。

图1-4 通过五类解决方案

1.2划分层次聚类

在划分方法中，观测值被分为K组并根据给定的规则改组成最有粘性的类。

1.2.1 K均值聚类

最常见的划分方法是K均值聚类分析。从概念上讲，K均值算法如下：

(1) 选择K个中心点（随机选择K行）；

(2) 把每个数据点分配到离它最近的中心点；

(3) 重新计算每类中的点到该类中心点距离的平均值（也就说，得到长度为p的均值向量，这里的p是变量的个数）；

(4) 分配每个数据到它最近的中心点；

(5) 重复步骤(3)和步骤(4)直到所有的观测值不再被分配或是达到最大的迭代次数（R把10次作为默认迭代次数）。

K均值聚类能处理比层次聚类更大的数据集。在R中K均值的函数格式是kmeans(x,centers)，这里x表示数值数据集（矩阵或数据框），centers是要提取的聚类数目。函数返回类的成员、类中心、平方和（类内平方和、类间平方和、总平方和）和类大小。

由于K均值聚类在开始要随机选择k个中心点，在每次调用函数时可能获得不同的方案。使用set.seed()函数可以保证结果是可复制的。此外，聚类方法对初始中心值的选择也很敏感。

kmeans()函数有一个nstart选项尝试多种初始配置并输出最好的一个。例如，加上nstart=25会生成25个初始配置。通常推荐使用这种方法。

不像层次聚类方法，K均值聚类要求你事先确定要提取的聚类个数。同样，NbClust包可以用来作为参考。另外，在K均值聚类中，类中总的平方值对聚类数量的曲线可能是有帮助的。可根据图中的弯曲选择适当的类的数量。

data(wine, package="rattle")

head(wine)

df <- scale(wine[-1])  

wssplot(df)      

library(NbClust)

set.seed(1234)

nc <- NbClust(df, min.nc=2, max.nc=15, method="kmeans")

par(opar)

table(nc$Best.n[1,])

barplot(table(nc$Best.n[1,]),

        xlab="Numer of Clusters", ylab="Number of Criteria",

        main="Number of Clusters Chosen by 26 Criteria")

set.seed(1234)

fit.km <- kmeans(df, 3, nstart=25)

fit.km$size

fit.km$centers                                               

aggregate(wine[-1], by=list(cluster=fit.km$cluster), mean)

 

图1-5 聚类个数对比

 

图1-6 推荐的聚类个数

1.2.2围绕中心点的划分

因为K均值聚类方法是基于均值的，所以它对异常值是敏感的。一个更稳健的方法是围绕中

心点的划分（PAM），K均值聚类一般使用欧几里得距离，而PAM可以使用任意的距离来计算。

PAM算法如下：

(1) 随机选择K个观测值（每个都称为中心点）；

(2) 计算观测值到各个中心的距离/相异性；

(3) 把每个观测值分配到最近的中心点；

(4) 计算每个中心点到每个观测值的距离的总和（总成本）；

(5) 选择一个该类中不是中心的点，并和中心点互换；

(6) 重新把每个点分配到距它最近的中心点；

(7) 再次计算总成本；

(8) 如果总成本比步骤(4)计算的总成本少，把新的点作为中心点；

(9) 重复步骤(5)～(8)直到中心点不再改变。

可以使用cluster包中的pam()函数使用基于中心点的划分方法。格式如下：

pam(x, k, metric="euclidean", stand=FALSE)

x表示数据矩阵或数据框，k表示聚类的个数，metric表示使用的相似性/相异性的度量，而stand是一个逻辑值，表示是否有变量应该在计算该指标之前被标准化。

对葡萄酒数据使用基于质心的划分方法：

library(cluster)

set.seed(1234)

fit.pam <- pam(wine[-1], k=3, stand=TRUE)      #聚类数据的标准化

fit.pam$medoids    #输出中心点

 

图1-8 实际的观测值

clusplot(fit.pam, main="Bivariate Cluster Plot")        #画出聚类方案

 

图1-7 PAM算法得到的三组聚类图

1.2.3避免不存在的类

聚类分析是一种旨在识别数据集子组的方法，并且在此方面十分擅长，甚至可以发现不存在的类。

library(fMultivar)

set.seed(1234)

df <- rnorm2d(1000, rho=.5)

df <- as.data.frame(df)

plot(df, main="Bivariate Normal Distribution with rho=0.5"

 

 

图1-8 二元正态数据，该数据集中无类

随后使用wssplot()和Nbclust()函数来确定当前聚类的个数：

wssplot(df)

library(NbClust)

nc <- NbClust(df, min.nc=2, max.nc=15, method="kmeans")

par(opar)

barplot(table(nc$Best.n[1,]),

        xlab="Numer of Clusters", ylab="Number of Criteria",

main  ="Number of Clusters Chosen by 26 Criteria")

图1-9 推荐的聚类数

Wassplot()函数建议聚类个数是3,然而Nbclust函数返回的准则多数支持2类或3类，代码如下：

library(ggplot2)

library(cluster)

fit <- pam(df, k=2)

df$clustering <- factor(fit$clustering)

ggplot(data=df, aes(x=V1, y=V2, color=clustering, shape=clustering)) +geom_point() + ggtitle("Clustering of Bivariate Normal Data")

plot(nc$All.index[,4], type="o", ylab="CCC",

     xlab="Number of clusters", col="blue")

图1-9 PAM聚类分析，提取两类

NbClust包中的立方聚类规则，往往可以解释不存在的结构，代码如下：

plot(nc$All.index[,4], type="o", ylab="CCC",

     xlab="Number of clusters", col="blue")

 

 

结果如图所示，当CCC的值为负并且对于两类或是更多的类递减时，就是典型的单峰分布。

1. 分类

2.1  分类概述

分类(classification )是这样的过程：它找出描述并区分数据类或概念的模型(或函数)，以便能够使用模型预测类标记未知的对象类。分类分析在数据挖掘中是一项比较重要的任务,目前在商业上应用最多。分类的目的是学会一个分类函数或分类模型(也常常称作分类器),该模型能把数据库中的数据项映射到给定类别中的某一个类中。

1. 分类与聚类的差异：

分类和回归都可用于预测，两者的目的都是从历史数据纪录中自动推导出对给定数据的推广描述，从而能对未来数据进行预测。与回归不同的是，分类的输出是离散的类别值，而回归的输出是连续数值。二者常表现为决策树的形式，根据数据值从树根开始搜索，沿着数据满足的分支往上走，走到树叶就能确定类别。

1. 分类器：

构造分类器，需要有一个训练样本数据集作为输入。训练集由一组数据库记录或元组构成，每个元组是一个由有关字段(又称属性或特征)值组成的特征向量，此外，训练样本还有一个类别标记。一个具体样本的形式可表示为：(v1,v2,...,vn; c)；其中vi表示字段值，c表示类别。分类器的构造方法有统计方法、机器学习方法、神经网络方法等等。

1. 不同的分类器的特点：

不同的分类器有不同的特点。有三种分类器评价或比较尺度：

• 预测准确度；
• 计算复杂度；
• 模型描述的简洁度。预测准确度是用得最多的一种比较尺度，特别是对于预测型分类任务。计算复杂度依赖于具体的实现细节和硬件环境，在数据挖掘中，由于操作对象是巨量的数据，因此空间和时间的复杂度问题将是非常重要的一个环节。对于描述型的分类任务，模型描述越简洁越受欢迎。

另外要注意的是，分类的效果一般和数据的特点有关，有的数据噪声大，有的有空缺值，有的分布稀疏，有的字段或属性间相关性强，有的属性是离散的而有的是连续值或混合式的。目前普遍认为不存在某种方法能适合于各种特点的数据。

1. 聚类与分类的差别与联系

聚类(clustering)是指根据“物以类聚”的原理，将本身没有类别的样本聚集成不同的组，这样的一组数据对象的集合叫做簇，并且对每一个这样的簇进行描述的过程。它的目的是使得属于同一个簇的样本之间应该彼此相似，而不同簇的样本应该足够不相似。与分类规则不同，进行聚类前并不知道将要划分成几个组和什么样的组，也不知道根据哪些空间区分规则来定义组。其目的旨在发现空间实体的属性间的函数关系，挖掘的知识用以属性名为变量的数学方程来表示。

当前，聚类技术正在蓬勃发展，涉及范围包括数据挖掘、统计学、机器学习、空间数据库技术、生物学以及市场营销等领域，聚类分析已经成为数据挖掘研究领域中一个非常活跃的研究课题。常见的聚类算法包括：K-均值聚类算法、K-中心点聚类算法、CLARANS、BIRCH、CLIQUE、DBSCAN等。

2.2  常见的分类算法

2.2.1  逻辑回归

logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w'x+b（w'表示w的转置），其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w'x+b作为因变量，即y =w'x+b，而logistic回归则通过函数L将w'x+b对应一个隐状态p，p =L(w'x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。

logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。

Logistic回归实质：发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。

2.2.2  决策树

决策树(decision tree)是一种基本的分类与回归方法。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布，如图2.1所示的为简单的决策树：

图2.1  简单的决策树

其主要优点是模型具有可读性，分类速度快。学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型。预测时，对新的数据，利用决策树模型进行分类。

决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪。

决策树的典型算法有ID3，C4.5，CART等。

国际权威的学术组织，数据挖掘国际会议ICDM （the IEEE International Conference on Data Mining）在2006年12月评选出了数据挖掘领域的十大经典算法中，C4.5算法排名第一。C4.5算法是机器学习算法中的一种分类决策树算法,其核心算法是ID3算法。C4.5算法产生的分类规则易于理解，准确率较高。不过在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，在实际应用中因而会导致算法的低效。

决策树算法的优点如下：

1. 分类精度高；
2. 生成的模式简单；
3. 对噪声数据有很好的健壮性。

因而是目前应用最为广泛的归纳推理算法之一，在数据挖掘中受到研究者的广泛关注。

决策树基本思想：

1. 树以代表训练样本的单个结点开始。
2. 如果样本都在同一个类．则该结点成为树叶，并用该类标记。
3. 否则，算法选择最有分类能力的属性作为决策树的当前结点．
4. 根据当前决策结点属性取值的不同，将训练样本数据集tlI分为若干          子集，每个取值形成一个分枝，有几个取值形成几个分枝。匀针对上一步得到的一个子集，重复进行先前步骤，递4'I形成每个划分样本上的决策树。一旦一个属性出现在一个结点上，就不必在该结点的任何后代考虑它。
5. 递归划分步骤仅当下列条件之一成立时停止：

①  给定结点的所有样本属于同一类。

②  没有剩余属性可以用来进一步划分样本．在这种情况下．使用多数表决，将给定的结点转换成树叶，并以样本中元组个数最多的类别作为类别标记，同时也可以存放该结点样本的类别分布，

③  如果某一分枝tc，没有满足该分支中已有分类的样本，则以样本的多数类创建一个树叶。

2.2.3  随机森林

（1） 什么是随机森林

集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成单预测，因此优于任何一个单分类的做出预测。

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

1. 随机森林的过程、优势

1. 根据下列算法而建造每棵树：

用N来表示训练用例（样本）的个数，M表示特征数目。

输入特征数目m，用于确定决策树上一个节点的决策结果；其中m应远小于M。

从N个训练用例（样本）中以有放回抽样的方式，取样N次，形成一个训练集（即bootstrap取样），并用未抽到的用例（样本）作预测，评估其误差。

1. 为什么要随机抽样训练集？

如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的

1. 为什么要有放回地抽样？

如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“片面的”（当然这样说可能不对），也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

1. 随机森林的优点

在当前所有算法中，具有极好的准确率，能够有效地运行在大数据集上，能够处理具有高维特征的输入样本，而且不需要降维，能够评估各个特征在分类问题上的重要性，对于缺省值问题也能够获得很好得结果。

2.2.4  支持向量机

支持向量机（Support Vector Machine ,SVM）的主要思想是：建立一个最优决策超平面，使得该平面两侧距离该平面最近的两类样本之间的距离最大化，从而对分类问题提供良好的泛化能力。对于一个多维的样本集，系统随机产生一个超平面并不断移动，对样本进行分类，直到训练样本中属于不同类别的样本点正好位于该超平面的两侧，满足该条件的超平面可能有很多个，SVM正式在保证分类精度的同时，寻找到这样一个超平面，使得超平面两侧的空白区域最大化，从而实现对线性可分样本的最优分类。

支持向量机中的支持向量（Support Vector）是指训练样本集中的某些训练点，这些点最靠近分类决策面，是最难分类的数据点。SVM中最优分类标准就是这些点距离分类超平面的距离达到最大值；“机”（Machine）是机器学习领域对一些算法的统称，常把算法看做一个机器，或者学习函数。SVM是一种有监督的学习方法，主要针对小样本数据进行学习、分类和预测，类似的根据样本进行学习的方法还有决策树归纳算法等。

SVM的优点：

1. 不需要很多样本，不需要有很多样本并不意味着训练样本的绝对量很少，而是说相对于其他训练分类算法比起来，同样的问题复杂度下，SVM需求的样本相对是较少的。并且由于SVM引入了核函数，所以对于高维的样本，SVM也能轻松应对。
2. 结构风险最小。这种风险是指分类器对问题真实模型的逼近与问题真实解之间的累积误差。
3. 非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也叫惩罚变量）和核函数技术来实现，这一部分也正是SVM的精髓所在。

线性分类：

对于最简单的情况，在一个二维空间中，要求把下图所示的白色的点和黑色的点集分类，显然，下图中的这条直线可以满足我们的要求，并且这样的直线并不是唯一的。如图2.2所示：

 

 

图2.2  简单的点集分类

对于最简单的情况，在一个二维空间中，要求把下图所示的白色的点和黑色的点集分类，显然，下图中的这条直线可以满足我们的要求，并且这样的直线并不是唯一的，如图2.3所示：

图2.3  多种简单的点集直线

那么哪条直线才是最优的呢？就是分类两侧距离决策直线距离最近的点离该直线综合最远的那条直线，即分割的间隙越大越好，这样分出来的特征的精确性更高，容错空间也越大。这个过程在SVM中被称为最大间隔（Maximum Marginal）。下图红色和蓝色直线之间的间隙就是要最大化的间隔，显然在这种情况下，分类直线位于中间位置时可以使得最大间隔达到最大值，如图2.4所示：

图2.4  svm中的最大距离

线性不可分：

现实情况中基于上文中线性分类的情况并不具有代表性，更多情况下样本数据的分布式杂乱无章的，这种情况下，基于线性分类的直线分割面就无法准确完成分割。如图2.5所示，在黑色点集中掺杂有白色点，白色点集中掺杂有黑色点的情况：

图2.5  杂乱无章的样本

对于这种非线性的情况，一种方法是使用一条曲线去完美分割样品集，从二维空间扩展到多维，可以使用某种非线性的方法，让空间从原本的线性空间转换到另一个维度更高的空间，在这个高维的线性空间中，再用一个超平面对样本进行划分，这种情况下，相当于增加了不同样本间的区分度和区分条件。在这个过程中，核函数发挥了至关重要的作用，核函数的作用就是在保证不增加算法复杂度的情况下将完全不可分问题转化为可分或达到近似可分的状态。

 

图2.6  将难以分割的放到更高的维度

图2.6所示的左侧红色的点和绿色的点在二维空间中，绿色的点被红色点包围，线性不可分，但是扩展到三维（多维）空间后，可以看到，红绿色点间Z方向的距离有明显差别，同种类别间的点集有一个共同特征就是他们基本都在一个面上，所以借用这个区分，可以使用一个超平面对这两类样本进行分类，如上图中黄色的平面。

线性不可分映射到高维空间，可能导致很高的维度，特殊情况下可能达到无穷多维，这种情况下会导致计算复杂，伴随产生惊人的计算量。但是在SVM中，核函数的存在，使得运算仍然是在低维空间进行的，避免了在高维空间中复杂运算的时间消耗。

SVM另一个巧妙之处是加入了一个松弛变量来处理样本数据可能存在的噪声问题，如图2.7所示：

 

 

 

图2.7  SVM算法允许偏移量

SVM允许数据点在一定程度上对超平面有所偏离，这个偏移量就是SVM算法中可以设置的outlier值，对应于上图中黑色实线的长度。松弛变量的加入使得SVM并非仅仅是追求局部效果最优，而是从样本数据分布的全局出发，统筹考量，正所谓成大事者不拘小节。

2.3  数据准备

在开始分类之前，首先需要准备的包有rpart、rpart.plot和party包来实现决策树模型以及可视化，通过randomForest包拟合随机森林，通过e1071包构造支持向量机，通过R中的基本函数glm()实现逻辑回归。

需要准备的数据集是威斯康星州乳腺癌数据，威斯康星州乳腺癌数据集是一个由逗号分割的txt文件，本数据集包含699个细针抽吸活检的样本单元，其中458个为良性的样本单元，241个为恶性单元，总计有11个变量。

数据集找寻网址：

Index of /ml/machine-learning-databases

数据集包含的变量包括：

肿块厚度、细胞大小的均匀性、细胞形状的均匀性、边际附着力、单个上皮细胞大小、裸核、乏味染色体、正常核、有丝分裂、类别。

数据处理（得到训练数据集：df.train，验证数据集：df.validate）：

loc <- "http://archive.ics.uci.edu/ml/machine-learning-databases/"

#  数据从UCI数据库当中抽取

ds  <- "breast-cancer-wisconsin/breast-cancer-wisconsin.data"

#  选取数据集breast-cancer-wisconsin

url <- paste(loc, ds, sep="")

breast <- read.table(url, sep=",", header=FALSE, na.strings="?")

# header
一个表示文件是否在第一行包含了变量的逻辑型变量。
如果header设置为TRUE，则要求第一行要比数据列的数量少一列。

# na.strings
可选的用于表示缺失值的字符向量。

names(breast) <- c("ID", "clumpThickness", "sizeUniformity",

                   “肿块厚度” “细胞大小的均匀性”

 "shapeUniformity", "maginalAdhesion",

                  “细胞形状的均匀性” “边际附着力”

 "singleEpithelialCellSize", "bareNuclei",

                  “单个上皮细胞大小” “裸核”

 "blandChromatin", "normalNucleoli", "mitosis", "class")

“乏味染色体”   “正常核”    “有丝分裂” “类别”

df <- breast[-1]

#  剔除第一列

根据变量位置

breast$v1 <- NULL

df$class<-factor(df$class,levels=c(2,4),labels=c("benign","malignant")) “良性”  “恶性”

训练集数据生成

set.seed(1234)

train <- sample(nrow(df), 0.7*nrow(df))

# nrow(df) 表示数据集df的行数，因为df数据集一行为一小组，所以按行来取，倘若需要按列来取，则使用nrow（）

从数据集df所有行中随机抽取70%行数作为样本

df.train <- df[train,]

#  训练数据集（70%的数据）

df.validate <-4

#  验证数据集

table(df.train$class)

table(df.validate$class)

2.4  逻辑回归

R中的基本函数glm()可用于拟合逻辑回归模型，glm()函数自动将预测变量中的分类变量编码为响应的虚拟变量，威斯康星州乳腺癌数据中的全部预测变量都是数值变量，因此不必要对其编码，，在R中实现的代码为：

fit.logit <- glm(class~., data = df.train, family = binomial())

#  以类别为响应变量，其余变量为预测变量

summary(fit.logit)

#  基于df.train数据框中的数据构造逻辑回归模型，并给出模型中的系数如图2.8所示：

 

 

图2.8  回归模型中的相关系数

#  接着，采用基于df.train建立的模型来对df.validate数据集中的样本单元分类。Predict()函数默认输出肿瘤为恶性的对数概率，指定参数type=”response”即可得到预测肿瘤为恶性的概率。

prob <- predict(fit.logit, df.validate, type="response")

logit.pred <- factor(prob > .5, levels=c(FALSE, TRUE),

                     labels=c("benign", "malignant"))

#  给出预测与实际情况对比表（混淆矩阵）

logit.perf <- table(df.validate$class, logit.pred,

                    dnn=c("Actual", "Predicted"))

logit.perf

混淆矩阵如图2.9所示：

其对应的预测准确率为（129+69）/205 = 0.9658

2.5  决策树

2.5.1  经典决策树

经典决策树以一个二元输出变量（肿瘤恶性/良性）和一组预测变量（对应9个细胞特征）为基础，具体算法如下：

1. 选定一个最佳预测变量将全部样本单元分为两类，实现两类纯度最大化（一类中良性的样本尽可能多，一类中恶性的样本尽可能多）。如果预测变量连续，则选定一个分割点进行分类，使得两类纯度最大化；如果预测变量为分类变量，则对各类别合并在进行分类。
2. 对每一个类别继续执行步骤（1）
3. 重复上面两步，直到子类别中所含的单元样本数过少，或者没有其它分类法能将不纯度下降到一个给定的阈值以下即可。
4. 对任一样本单元执行决策树，根据（3）得到模型预测的所属类别。

下面是通过rpart()函数创建分类决策树：
library(rpart)

#  选用随机数种子

set.seed(1234)    

#  rpart()函数生成决策树      

dtree <- rpart(class ~ ., data=df.train, method="class",      

               parms=list(split="information"))

dtree$cptable

plotcp(dtree)

#   使用plotcp（）画出交叉验证误差与复杂度参数关系图图如图2.9所示：

 

 

 

图2.9  交叉验证误差与复杂度参数关系图

#  剪枝

dtree.pruned <- prune(dtree, cp=.0125)

#  使用prune（dtree, cp=0.0125)可以得到一个理想的树

library(rpart.plot)

prp(dtree.pruned, type = 2, extra = 104,  

    fallen.leaves = TRUE, main="Decision Tree")

#  prp函数可用于画出最终的决策树，从树的顶端开始，如果条件成立则左枝往下，否则右枝往下，如图2.10所示：

图2.10   使用prp函数画出最终决策树

#  predict（）函数用于对验证集中的观测点分类

dtree.pred <- predict(dtree.pruned, df.validate, type="class")

dtree.perf <- table(df.validate$class, dtree.pred,

                    dnn=c("Actual", "Predicted"))

dtree.perf

#  对应生成的混淆矩阵如图2.11所示：

图2.11   使用决策树得到的混淆矩阵

可以看到其预测准确率为（69+129）/210 = 0.942

 

2.5.2  条件推断树

条件推断树是传统决策树的一种重要的变体，它与传统的决策树类似，但变量的选取和分割是基于显著性检验的。条件推断树的算法如下：

1. 对输出变量与每个预测变量间的关系计算p值。
2. 选取p值最小的变量。
3. 在因变量与被选中的变量间尝试所有可能的二元分割，并选取最显著的分割。
4. 将数据集分成两群，并在子群重复上述步骤。
5. 重复直到所有分割都不显著。

可以通过party包中的ctree()函数生成条件推断树，在R中的实现代码如下所示：

library(party)

fit.ctree <- ctree(class~., data=df.train)

plot(fit.ctree, main="Conditional Inference Tree")

#  生成的条件推断树如图2.12所示：

图2.12   乳腺癌数据的条件推断树

ctree.pred <- predict(fit.ctree, df.validate, type="response")

ctree.perf <- table(df.validate$class, ctree.pred,

                    dnn=c("Actual", "Predicted"))

ctree.perf

#  其对应生成的混淆矩阵如图2.13所示：

图2.13   使用推断树得到的混淆矩阵

可以看到其预测准确率为（67+131）/210 = 0.942

2.6  随机森林

在随机森林当中，我们同时生成多个预测模型，并将模型的结果汇总以提升分类的准确率。

结合上面关于随机森林的介绍，我们可以知道随机森林涉及对样本单元和变量进行抽样，从而生成大量的决策树，以所有决策树预测类别中众数类别即为随机森林所预测的这一样本单元。结合分类算法中随机森林的介绍，我们在R里面处理乳腺癌的数据，在R中实现的代码如下所示：

#   在R中randomForest包中的randomForest()函数可用于生成随机森 林，函数默认生成500棵树
library(randomForest)

set.seed(1234)

#   首先randomForest()函数从训练集当中有放回的随机抽取489个观测点，在每一个节点随机抽取3个变量，生成500棵传统决策树。

fit.forest <- randomForest(class~., data=df.train,        

                           na.action=na.roughfix,

                           importance=TRUE)             

fit.forest

#   如图2.14所示的是fit.forest（随机森林）产生的结果：

图2.14   乳腺癌样本数据对应的随机森林

#   我们可以通过调整参数importance=TRUE来度量变量的重要性，并通过 importance()输出，在R中的输出结果如图2.15所示：

importance(fit.forest, type=2)

 

 

图2.14   给出变量的重要性

#  对训练集外的样本集进行分类，最后得到的随机森林的混淆矩阵如2.15所示：

forest.pred <- predict(fit.forest, df.validate)         

forest.perf <- table(df.validate$class, forest.pred,

                     dnn=c("Actual", "Predicted"))

forest.perf

 

图2.15   随机森林对应的混淆矩阵

可以看到其预测准确率为（128+68）/205 = 0.956

2.7  支持向量机

支持向量机（SVM）旨在在多维空间找到一个能将全部样本单元分成两类的最优平面的过程。在R中SVM可以通过kernlab包的ksvm()函数和e1071包中的svm()函数实现，在R中实现乳腺癌样本数据的支持向量机代码如下所示：

#  导入SVM所需的包

library(e1071)

set.seed(1234)

fit.svm <- svm(class~., data=df.train)

fit.svm

#  训练集的支持向量机结果如图2.16所示：

图2.16   训练集的支持向量机结果

svm.pred <- predict(fit.svm, na.omit(df.validate))

svm.perf <- table(na.omit(df.validate)$class,

                  svm.pred, dnn=c("Actual", "Predicted"))

svm.perf

#   我们通过训练集的支持向量机预测测试集的准确率，如图2.17所示：

图2.17   测试集的混淆矩阵

可以看到其预测准确率为（126+70）/205 = 0.956

选择调和参数：

SVM()函数默认通过径向基函数将样本单元投射到高维空间，在用带RBF核的SVM拟合样本时，这里会有两个参数：

参数degree：

在多项式核中使用，表示使用的多项式的阶数。

参数gamma：

对于多项式核，它是多项式核函数

中的γ \gammaγ。

对于高斯核，它是径向基函数中的2σ /1

下面给出乳腺癌数据带核的SVM模型，在R中的实现如下所示：

set.seed(1234)

#  变换参数，对不同的gamma和成本拟合一个带RBF核的SVM模型，总共尝试8个不同的gamma(从0.000001到10)以及21个成本参数。

tuned <- tune.svm(class~., data=df.train,

                  gamma=10^(-6:1),

                  cost=10^(-10:10))

#  输出最优模型

Tuned

#  拟合模型所用参数

fit.svm <- svm(class~., data=df.train, gamma=.01, cost=1)

svm.pred <- predict(fit.svm, na.omit(df.validate))

svm.perf <- table(na.omit(df.validate)$class,

                  svm.pred, dnn=c("Actual", "Predicted"))

#  评估交叉验证的表现如图2.18所示：

svm.perf

可以看到其预测准确率为（128+70）/205 = 0.965

相比不选择调和参数的模型来比较，加调和参数之后对预测数据集的预测更加好。