二维卷积层入门：卷积运算、填充与步幅、输入输出通道

微信公号：ilulaoshi / 原文发表在我的个人网站：https://lulaoshi.info/machine-learning/convolutional/two-dimension-convolution-layer.html
转载请引用我的个人网站链接，谢谢！

卷积神经网络（Convolutional Neural Network，CNN）在图像领域应用非常广泛。区别于普通的全连接前馈神经网络，卷积神经网络是含有卷积层（Convolutional Layer）的神经网络。本文解释二维卷积层的工作原理。

卷积的数学表示

其实计算机、电子、通信类专业的毕业生应该都对“卷积”一词有所耳闻，卷积是数字信号处理中一定会介绍的概念，但是本科毕业多年，这些基础知识早都忘光了。关于深度学习中的卷积，再次接触他就是是在Ian Goodfellow的《Deep Learning》一书中。这本书，以及曾经的本科课本中对卷积的定义都是一个非常不直观的数学公式。
$$f\ast g(n)={\int }_{-\infty }^{+\infty }f(\tau )g(n-\tau )d\tau$$
这个公司表示$f$和$g$做卷积，似乎公式中有个乘法：即$f(\tau )$和$g(n-\tau )$做了个乘法。但$n$和$n-\tau$是什么意思似乎不太好理解。

上面公式是连续的定义，再看看离散的定义：
$$f\ast g(n)=\sum _{\tau =-\infty }^{+\infty }f(\tau )g(n-\tau ).$$

相信看到这两个公式后，绝大多数朋友就想直接放弃了。但不要太丧气，卷积其实没有那么难。

互相关运算

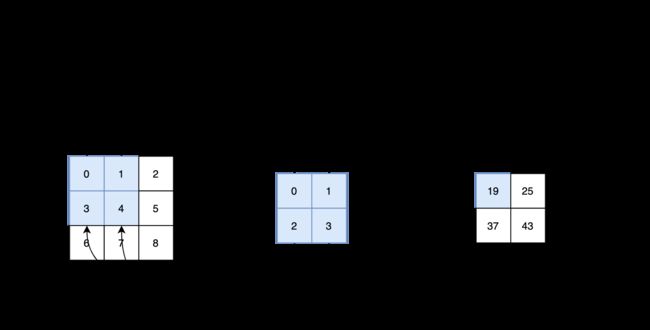
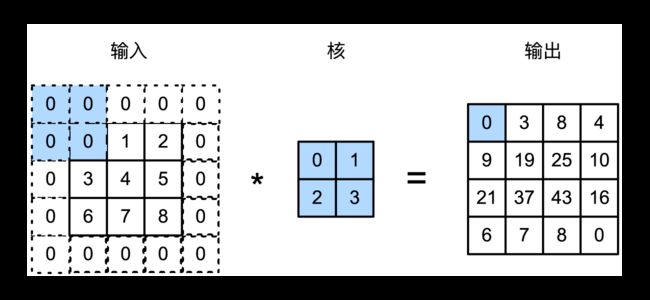
我们从一个更为简单的角度来看：一个二维的卷积其实是两个矩阵之间的某种乘法。《动手学深度学习》举了一个例子，即图1：两个二维的矩阵做某种特殊的乘法，输出的第一个元素是这么得到的：$0\times 0+1\times 1+3\times 2+4\times 3=19$。也就是说，核矩阵与输入矩阵中深色部分一一相乘，再加起来。

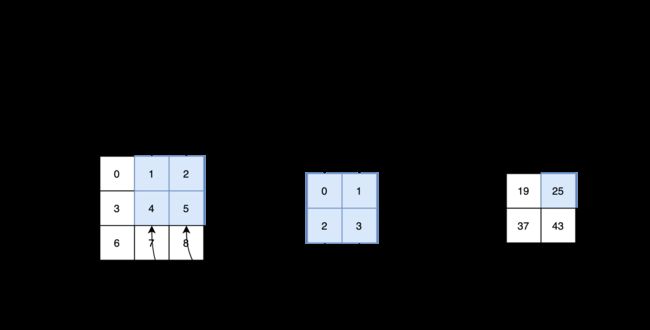
接着，我们向右移动输入矩阵的深色部分，得到第二个输出元素。同样，计算的过程也是输入矩阵的深色部分与核一一相乘。

具体而言，输出中的各个元素是按照下面的公式计算的：
$$\begin{gathered} 0\times 0+1\times 1+3\times 2+4\times 3=19, \\ 1\times 0+2\times 1+4\times 2+5\times 3=25, \\ 3\times 0+4\times 1+6\times 2+7\times 3=37, \\ 4\times 0+5\times 1+7\times 2+8\times 3=43. \end{gathered}$$

用动图演示，输入矩阵和核矩阵之间的卷积操作大概如图3所示：

图1和图2中，输入矩阵与核矩阵之间的相乘被称作为互相关（Cross-Correlation）运算。

互相关与卷积

一些深度学习教程都使用这种互相关运算来解释卷积的计算过程。但实际上，上述计算过程并非学术上严格意义上的卷积。

我们将这种互相关的矩阵乘法转换成公式，如果输入矩阵为$I$，核矩阵为$K$，核矩阵$K$形状为$m\times n$。我们想要得到输出矩阵$O$中$(i,j)$位置的元素，其实就是对矩阵中各个数字做乘法，最后累加到一起。
$$O(i,j)=(K\ast I)(i,j)=\sum _m\sum _{n}I(i+m,j+n)K(m,n)$$
上面公式中，$I(i+m,j+n)K(m,n)$表示输入矩阵的某个元素$I(i+m,j+n)$与核矩阵的元素$K(m,n)$相乘。${\sum }_m$和${\sum }_n$分别在矩阵的横向和纵向做累加。

但这个公式依然与最初看到的卷积公式有些区别，我们将输入矩阵的加号改为减号：
$$O(i,j)=(K\ast I)(i,j)=\sum _m\sum _{n}I(i-m,j-n)K(m,n)$$
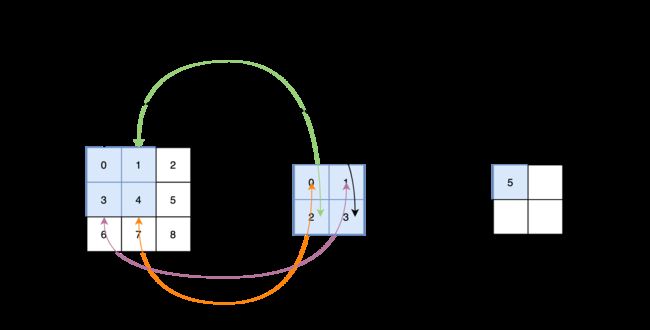
这就出现了卷积公式中的减号，那么这两个矩阵实际的计算类似于：

也就是说，输入矩阵深色区域的最后一个元素与核矩阵的第一个元素相乘，输入矩阵深色区域的倒数第二个元素与核矩阵的第二个元素相乘，以此类推…又或者说，把核矩阵旋转180度，再与输入矩阵相乘。

卷积数学公式中的减号，在二维矩阵的场景下，可以被解释为：先旋转、再相乘。由于在深度学习中，核矩阵是一个需要训练的参数，卷积神经网络都是针对图像，图像即使旋转180度，对于计算机来说区别不大。旋转与否，或者说是否使用减号，对于深度学习来说关系不大，反而不旋转的互相关运算计算起来更方便。因此，很多深度学习框架直接使用互相关运算来表示卷积的过程。

卷积在图像领域的功能

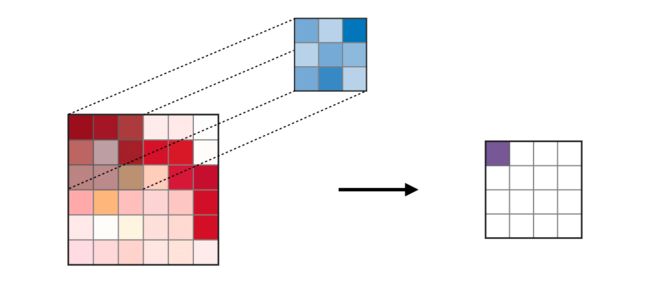
在图像和计算机视觉领域，卷积其实已经有几十年的发展历史。在传统的计算机视觉和模式识别中，卷积又被称为滤波器（Filter）。对一张图片，进行卷积操作，可以得到很多种神奇的效果。图5来自维基百科，最上面是卷积核是一个单位矩阵，使用单位矩阵对原图进行卷积操作，得到的输出与原图一样；接下来的几个卷积核可以检测到物体边缘，或者进行锐化和模糊。

经过多年的研究，人们已经能够设计出不同的核矩阵，对图片进行转换，以达到不同的效果。不过，在深度学习出现之前，卷积核是人工设计的，当然需要消耗大量的时间和精力。

感谢梯度下降和反向传播，深度学习的出现使得不再需要人工设计卷积核。在卷积神经网络里，卷积核在初始化的时候是一些随机值，经过了训练，核矩阵是可以被学习出来的。或者说，卷积核是一些参数，可以通过机器学习训练得到。图6展示了不同的5*5卷积核经过梯度下降法的训练，不断更新变化的过程。

填充与步幅

至此，我们简单了解到在深度学习中，对输入矩阵进行卷积一般是使用一个卷积核进行互相关运算。图1和图2中，我们使用高和宽为3的输入与高和宽为2的卷积核得到高和宽为2的输出。一般来说，假设输入形状是$n_h\times n_w$，卷积核形状是$k_h\times k_w$，那么输出形状将会是$(n_h-k_h+1)\times (n_w-k_w+1)$。

卷积层的输出形状由输入形状和卷积核形状决定。接下来我们将介绍卷积层的两个超参数：填充（Padding）和步幅（Strides）。

填充 Padding

Padding是指在输入高和宽的两侧填充元素（通常是0）。我们在图1和图2的基础上，在输入高和宽的两侧分别添加了值为0的元素，使得输入高和宽从3变成了5，进而导致输出高和宽由2增加到4。图7中的输出矩阵第一个元素及其计算过程为：$0\times 0+0\times 1+0\times 2+0\times 3=0$。

一般来说，如果在高的两侧一共填充$p_h$行，在宽的两侧一共填充$p_w$列，那么输出形状将会是$(n_h-k_h+p_h+1)\times (n_w-k_w+p_w+1)$。也就是说，输出的高和宽会分别增加$p_h$和$p_w$。

在很多情况下，我们会设置$p_h=k_h-1$和$p_w=k_w-1$来使输入和输出具有相同的高和宽。这样会方便在构造网络时推测每个层的输出形状。假设这里$k_h$是奇数，我们会在高的两侧分别填充$p_h/2$行。如果$k_h$是偶数，一种可能是在输入的顶端一侧填充$\lceil p_h/2\rceil$行，而在底端一侧填充$\lfloor p_h/2\rfloor$行。宽的两侧填充同理。

卷积神经网络经常使用奇数高宽的卷积核，如1、3、5和7，所以两端上的填充个数相等。对任意的二维数组X，设它的第i行第j列的元素为X[i,j]。当两端上的填充个数相等，并使输入和输出具有相同的高和宽时，我们就知道输出Y[i,j]是由输入以X[i,j]为中心的窗口同卷积核进行互相关计算得到的。

步幅 Stride

前面图3演示的卷积例子中，卷积核矩阵从输入矩阵的左上方开始，按从左往右、从上往下的顺序，依次在输入矩阵上滑动。我们将每次滑动的行数和列数称为步幅（Stride）。

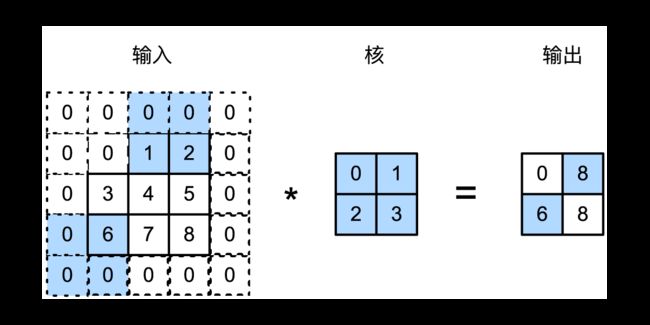
目前我们看到的例子里，在高和宽两个方向上步幅均为1。我们也可以使用更大的步幅。图8展示了在纵向上步幅为3、在横向上步幅为2的二维互相关运算。可以看到，输出第一列第二个元素时，卷积窗口向下滑动了3行，计算所使用元素为：$0\times 0+6\times 1+0\times 2+0\times 3=6$；而在输出第一行第二个元素时卷积窗口向右滑动了2列，计算所使用的元素为：$0\times 0+0\times 1+1\times 2+2\times 3=8$。当卷积窗口在输入上再向右滑动2列时，由于输入元素无法填满卷积核窗口，无结果输出。

一般来说，当高上步幅为$s_h$，宽上步幅为$s_w$时，输出形状为：$\lfloor (n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor (n_w-k_w+p_w+s_w)/s_w\rfloor$。

如果设置$p_h=k_h-1$和$p_w=k_w-1$，那么输出形状将简化为$\lfloor (n_h+s_h-1)/s_h\rfloor \times \lfloor (n_w+s_w-1)/s_w\rfloor$。更特殊的情况下，如果输入的高和宽能分别被高和宽上的步幅整除，那么输出形状将是$(n_h/s_h)\times (n_w/s_w)$。

如果我们令横向和纵向上的步幅均为2，相比输入矩阵，输出矩阵的高和宽会减半。

多输入通道和多输出通道

前面用到的输入矩阵和输出矩阵都是二维数组，但真实数据的维度经常更高。例如，彩色图像在高和宽2个维度外还有RGB（红、绿、蓝）3个颜色通道。假设彩色图像的高和宽分别是$h$和$w$（像素），那么它可以表示为一个$3\times h\times w$的高维数组。我们将大小为3的这一维称为通道（Channel）维。

多输入通道

当输入数据含多个通道时，我们构造的卷积核的输入通道数与输入数据的通道数相同，这样不同通道的卷积核能够与不同通道的输入数据做互相关运算。假设输入数据的通道数为$c_i$，那么卷积核的输入通道数同样为$c_i$。设卷积核形状为$k_h\times k_w$。在图3中，输入通道只有1维，$c_i=1$，知道卷积核只包含一个形状为$k_h\times k_w$的二维数组。当$c_i>1$时，我们将会为每个输入通道各分配一个形状为$k_h\times k_w$的核数组，即得到一个形状为$c_i\times k_h\times k_w$的卷积核。输入和卷积核各有$c_i$个通道，我们在各个通道上对输入的二维数组和卷积核的二维核数组做互相关运算，再将这$c_i$个互相关运算的输出按通道相加。

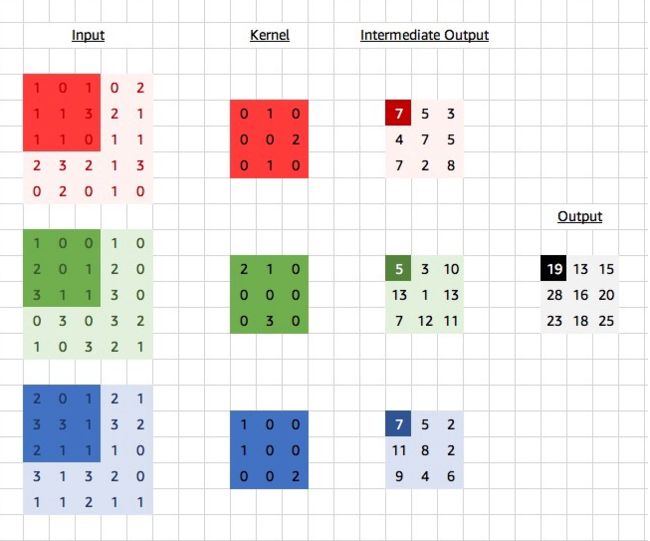
图9展示了含3个输入通道的二维互相关计算的例子，3个通道代表3种不同的颜色。在每个通道上，二维输入数组与二维卷积核做互相关运算，再按通道相加即得到输出。

多输出通道

除了输入通道可以大于等于1，输出通道也可以大于等于1。刚才提到，当输入通道有多个时，因为我们对各个通道的结果做了累加，所以不论输入通道数是多少，输出通道数总是为1。如果希望输出通道数大于1，那卷积核还要再增加一维。

设卷积核输入通道数和输出通道数分别为$c_i$和$c_o$，高和宽分别为$k_h$和$k_w$。输出通道数为1，$c_o=1$，卷积核实际上是$1\times c_i\times k_h\times k_w$。用图9里RGB三通道的例子来讲，卷积核形状为：$1\times 3\times 3\times 3$，即1个输出通道，3个输入通道，每个输入通道是$3\times 3$的矩阵。现在，我们希望输出通道数大于1，那就继续扩展卷积核的维度，将卷积核形状扩展形状即$c_o\times c_i\times k_h\times k_w$。在做互相关运算时，每个输出通道上的结果由卷积核在该输出通道上的核数组与整个输入数组计算而来。

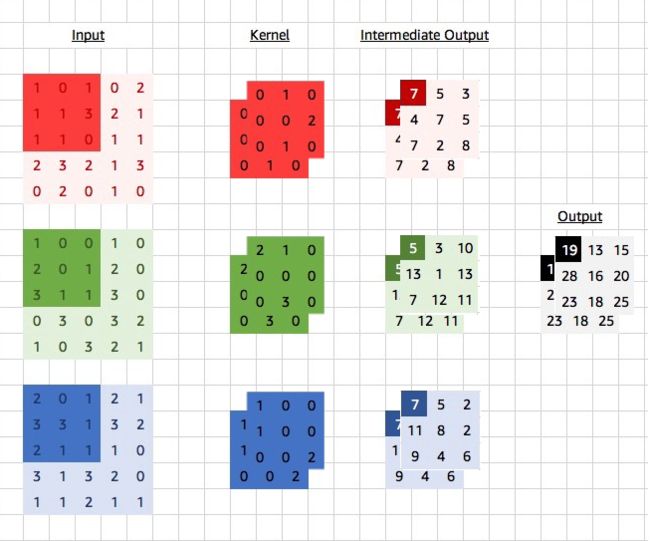
在图10的例子中，输入有3个RGB通道，卷积核也有RGB三个维度与之对应，为了增加输出通道数，卷积核在图9的基础上增加了一层。输入的深色部分与卷积核第一层进行卷积，得到输出中第一层结果，输入的深色部分与卷积核的第二层再进行卷积，得到第二层的结果，这样输出就有两层，或者说输出就在图9基础上增加了一维，又或者说输出通道数为2。可以说，输出通道数大于1时，还需要再使用多少倍的卷积核。

之所以要增加输出通道数，主要是一层卷积核无法覆盖图像的所有特征。比如下面的图11是对卷积核做了可视化，输出通道数为4，即共有4层卷积核，第一层主要在检测边缘和色差，第二层主要在检测旋转，第四层主要在检测狗的脸。

参考资料

1. https://www.deeplearningbook.org/contents/convnets.html
2. https://d2l.ai/chapter_convolutional-neural-networks/why-conv.html
3. https://zh.d2l.ai/chapter_convolutional-neural-networks/conv-layer.html
4. https://en.wikipedia.org/wiki/Kernel_(image_processing)
5. https://medium.com/apache-mxnet/multi-channel-convolutions-explained-with-ms-excel-9bbf8eb77108