神经网络与深度学习:人工神经网络(下)
人工神经网络(下)
- 1.小批量梯度下降法
-
- 1.1批量梯度下降
- 1.2随机梯度下降
- 1.3小批量梯度下降
- 2.梯度下降法的优化
-
- 2.1 小批量样本的选择
- 2.2 批量大小
- 2.3 学习率
- 2.4 梯度
- 3.Keras和tf.Keras
- 4. Sequential模型
-
- 3.1 搭建模型
- 3.2 配置训练方法
- 3.3 训练模型
- 3.4 评估模型
- 3.5 使用模型
- 5. 实例:实现手写数字识别
- 6. 模型的保存和加载
-
- 6.1 保存模型参数
- 6.2 加载模型参数
- 6.3 保存整个模型
- 6.4 加载模型
1.小批量梯度下降法
1.1批量梯度下降
Batch Gradient Descent,BGD
每次迭代都使用所有样本来计算偏导数;
由所有样本确定梯度方向;
每一步都是准确地向着极值点趋近,迭代次数少;
收敛于全局极小值或局部极小值点;
可以利用向量运算进行并行计算;
计算量大,训练时间长,不适合大规模数据集。

1.2随机梯度下降
Stochastic Gradient Descent,SGD
每次迭代只选择一个样本训练模型,使网络的输出尽可能逼近这个样本的标签值;
一轮:使用所有样本训练一遍;
反复训练多轮,直到网络对所有样本的误差足够小;
参数更新非常频繁,无法快速收敛;
不易于实现并行计算
1.3小批量梯度下降
Mini-Batch Gradient Descent,MBGD
小批量随机梯度下降(Mini-Batch SGD):
把数据分为多个小批量,每次迭代使用一个小批量来训练模型 ;
每个小批量中的所有样本共同决定了本次迭代中的梯度方向;
一轮:使用所有小批量训练一遍;
需要训练多轮,使网络对所有样本的误差足够小;
每次迭代的训练样本数固定,与整个训练集的样本数量无关;
可以实现并行运算;
训练大规模数据集。

2.梯度下降法的优化
梯度下降法:求解函数极值的方法。
非凸函数具有多个局部最优点,在局部极小值点,梯度接近于0,迭代停止,因此多层神经网络使用梯度下降法,无法保证一定可以达到全局最小值点。
影响小批量梯度下降法的因素:
2.1 小批量样本的选择

因为数据集的连续的样本之间有高度的相关性
所以在每轮训练之前,要打乱样本顺序。
2.2 批量大小
2.3 学习率

凸函数中,可以使用学习率衰减,开始训练时设置较大的学习率,加快收敛速度。在迭代过程中,学习率随着迭代次数逐渐减小,避免震荡 。
非凸函数中,可以周期性的增大学习率或自适应调整学习率。

2.4 梯度
①动量梯度下降法(Momentum)
动量=质量×速度
在更新参数时,可以在一定程度上保留之前的更新方向。
梯度方向不变:步长更大,收敛加快
梯度方向改变:步长变小,更新变慢

②牛顿加速梯度算法
(Nesterov Accelerated Gradient,NAG)
根据当前更新方向,估算下一步的梯度方向
在新位置计算梯度,修正梯度方向。

3.Keras和tf.Keras
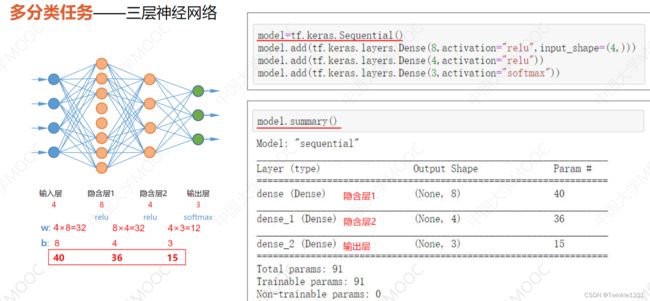
4. Sequential模型
3.1 搭建模型
3.2 配置训练方法
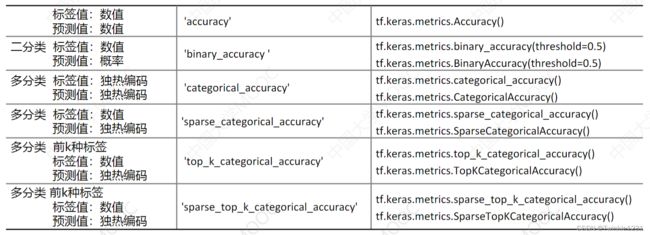
metrics:keras模型性能评估函数/自定义性能评估函数
3.3 训练模型
3.4 评估模型
3.5 使用模型
5. 实例:实现手写数字识别
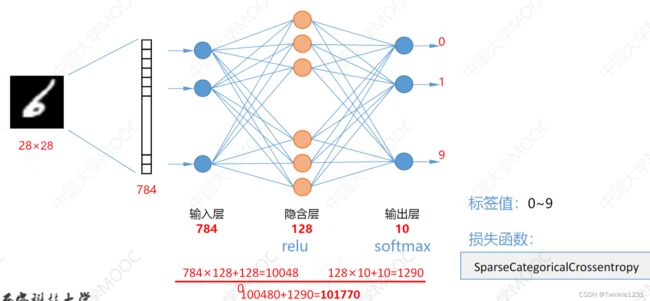
设计结构:
手写字体为28*28,展开为784的一维张量,因此输入层有784个单元。
输出层为10个单元,分别对应0-9(多分类任务),使用softmax
隐含层设计128个神经单元,使用relu
代码实现:
#导入库
from logging import logProcesses
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#加载数据
mnist=tf.keras.datasets.mnist
(train_x,train_y),(test_x,test_y)=mnist.load_data()
#数据预处理
# X_train=train_x.reshape((60000,28*28))
# X_test=test_x.reshape((10000,28*28))
# Convert two-dimensional array to one-dimensional array
X_train,X_test=tf.cast(train_x/255.0,tf.float32),tf.cast(test_x/255.0,tf.float32) #normalization
y_train,y_test=tf.cast(train_y,tf.int16),tf.cast(test_y,tf.int16)
#建立模型
model=tf.keras.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=(28,28))) #形状转换 变成一维数组
model.add(tf.keras.layers.Dense(128,activation='relu'))
model.add(tf.keras.layers.Dense(10,activation='softmax'))
#配置训练方法
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['sparse_categorical_accuracy'])
#训练模型
model.fit(X_train,y_train,batch_size=64,epochs=5,validation_split=0.2)
#评估模型
model.evaluate(X_test,y_test,verbose=2)
#使用模型
plt.axis('off')
plt.imshow(test_x[0],cmap='gray')
plt.show()
#测试集中的前四个数据
model.predict([[X_test[0]]])
np.argmax(model.predict([[X_test[0]]]))
for i in range(4):
plt.subplot(1,4,i+1)
plt.axis('off')
plt.imshow(test_x[i],cmap='gray')
plt.title(test_y[i])
plt.show()
model.predict(X_test[0:4])
np.argmax(model.predict(X_test[0:4]),axis=1)