【机器学习】EM 算法
在本文中规定,下凸函数为类似于 f ( x ) = x 2 f(x)=x^2 f(x)=x2 的函数,上凸函数为类似于 f ( x ) = − x 2 f(x)=-x^2 f(x)=−x2 的函数, f ( x ) = k x + b f(x)=kx+b f(x)=kx+b 这类线性函数既属于下凸函数又属于上凸函数,除去线性函数的下凸(或上凸)函数称为严格下凸(或上凸)函数。
Jensen 不等式
定义
若 f ( x ) f(x) f(x) 是区间 [ a , b ] [a,b] [a,b] 上的上凸函数,则对于任意的 x 1 , x 2 , … , x n ∈ [ a , b ] x_1,x_2,\dots,x_n\in[a,b] x1,x2,…,xn∈[a,b],有不等式
∑ i = 1 n f ( x i ) n ≤ f ( ∑ i = 1 n x i n ) \frac{\sum_{i=1}^nf(x_i)}{n}\le f\left( \frac{\sum_{i=1}^nx_i}{n} \right) n∑i=1nf(xi)≤f(n∑i=1nxi)
当且仅当 x 1 = x 2 = ⋯ = x n x_1=x_2=\dots=x_n x1=x2=⋯=xn 时等号恒成立。
更一般地,如果函数 f ( ⋅ ) f(·) f(⋅) 在函数 g ( ⋅ ) g(·) g(⋅) 的值域范围内是上凸的,不妨在 g ( ⋅ ) g(·) g(⋅) 的定义域内选取 n n n 个值 { x 1 , x 2 , … , x n } \{x_1,x_2,\dots,x_n\} {x1,x2,…,xn},那么
∑ i = 1 n λ i f ( g ( x i ) ) ≤ f ( ∑ i = 1 n λ i g ( x i ) ) (1) \sum_{i=1}^n \lambda_i f(g(x_i)) \le f\left( \sum_{i=1}^n \lambda_ig(x_i)\right) \tag{1} i=1∑nλif(g(xi))≤f(i=1∑nλig(xi))(1)
其中, λ i ≥ 0 \lambda_i\ge0 λi≥0 且 ∑ i = 1 n λ i = 1 \sum\limits_{i=1}^n \lambda_i=1 i=1∑nλi=1。式 ( 1 ) (1) (1) 被称为 Jensen 不等式(Jensen inequality)的一般形式。
式 ( 1 ) (1) (1) 也存在积分形式,这里不再列出。
当我们不考虑函数 g ( ⋅ ) g(·) g(⋅) 或者认为 g ( ⋅ ) = ⋅ g(·)=· g(⋅)=⋅ 时,式 ( 1 ) (1) (1) 可以化为
∑ i = 1 n λ i f ( x i ) ≤ f ( ∑ i = 1 n λ i x i ) (2) \sum_{i=1}^n \lambda_i f(x_i) \le f\left( \sum_{i=1}^n \lambda_ix_i\right)\tag{2} i=1∑nλif(xi)≤f(i=1∑nλixi)(2)
不妨认为 { λ i } \{\lambda_i\} {λi} 为随机变量 X = { x i } X=\{x_i\} X={xi} 的概率分布,那么式 ( 2 ) (2) (2) 可以进一步化为
E ( f ( X ) ) ≤ f ( E ( X ) ) (3) E(f(X))\le f(E(X))\tag{3} E(f(X))≤f(E(X))(3)
其中, E ( ⋅ ) E(·) E(⋅) 表示随机变量的期望。
通过一个简单的函数来理解 Jensen 不等式。
对于上凸函数 f ( x ) = − x 2 f(x)=-x^2 f(x)=−x2 ,存在如下图的两点 x 1 x_1 x1、 x 2 x_2 x2,满足 x 1 < x 2 x_1\lt x_2 x1<x2,根据上凸函数的性质可知 f ( x 1 ) + f ( x 2 ) 2 ≤ f ( x 1 + x 2 2 ) \frac{f(x_1)+f(x_2)}{2}\le f\left(\frac{x_1+x_2}{2}\right) 2f(x1)+f(x2)≤f(2x1+x2)。其中,不等式左侧 f ( x 1 ) f(x_1) f(x1) 和 f ( x 2 ) f(x_2) f(x2) 的均值可以理解为函数值的期望,不等式右侧 f ( x 1 + x 2 2 ) f\left(\frac{x_1+x_2}{2}\right) f(2x1+x2) 为 x i x_i xi 的期望的函数值,这与式 ( 2 ) (2) (2) 所表达的思想一致。
图 1 某上凸函数
类似地,对于下凸函数,根据其性质可知 E ( f ( X ) ) ≥ f ( E ( X ) ) E(f(X))\ge f(E(X)) E(f(X))≥f(E(X)) 。
式 ( 1 ) (1) (1) 给出了 Jensen 不等式的一般定义,而在 EM 算法中我们用到的是具体的 Jensen 不等式,即 f ( ⋅ ) = log ( ⋅ ) f(·)=\log(·) f(⋅)=log(⋅), g ( ⋅ ) = ⋅ g(·)=· g(⋅)=⋅ 情形下的 Jensen 不等式,由于 f ( ⋅ ) f(·) f(⋅) 为上凸函数,因此满足
∑ i = 1 n λ i log ( x i ) ≤ log ( ∑ i = 1 n λ i x i ) (4) \sum_{i=1}^n \lambda_i \log(x_i) \le \log\left( \sum_{i=1}^n \lambda_ix_i\right) \tag{4} i=1∑nλilog(xi)≤log(i=1∑nλixi)(4)
讨论对于 Jensen 不等式的一般定义式 ( 2 ) (2) (2) 中等号成立的条件。
若 f ( ⋅ ) f(·) f(⋅) 为严格上凸函数,则当且仅当 x 1 = x 2 = ⋯ = x n x_1=x_2=\dots=x_n x1=x2=⋯=xn 时等号成立;若 f ( ⋅ ) f(·) f(⋅) 为线性函数,则对于任意取值的 x i x_i xi 等号均成立,且不等式左侧恒等于右侧。故,若仅简单限制 f ( ⋅ ) f(·) f(⋅) 为上凸函数,则当且仅当 x 1 = x 2 = ⋯ = x n x_1=x_2=\dots=x_n x1=x2=⋯=xn 时等号成立。
证明
下面是对于上凸函数的 Jensen 不等式(即式 ( 2 ) (2) (2))证明。
(1) 首先对于 n = 1 n=1 n=1,很明显不等式成立;
(2) 对于 n = 2 n=2 n=2,由上凸函数图 1 1 1 可知, λ 1 f ( x 1 ) + λ 2 f ( x 2 ) ≤ f ( λ 1 x 1 + λ 2 x 2 ) \lambda_1f(x_1)+\lambda_2f(x_2)\le f(\lambda_1x_1+\lambda_2x_2) λ1f(x1)+λ2f(x2)≤f(λ1x1+λ2x2),不等式成立;
(3) 假设当 n = k n= k n=k 时,不等式成立,即 ∑ i = 1 k λ i f ( x i ) ≤ f ( ∑ i = 1 k λ i x i ) \sum\limits_{i=1}^k \lambda_i f(x_i) \le f\left( \sum\limits_{i=1}^k \lambda_ix_i\right) i=1∑kλif(xi)≤f(i=1∑kλixi)
下面证明 n = k + 1 n=k+1 n=k+1 时不等式成立即可:
∑ i = 1 k + 1 λ i f ( x i ) = λ k + 1 f ( x k + 1 ) + ∑ i = 1 k λ i f ( x i ) ( ① ) = λ k + 1 f ( x k + 1 ) + ( 1 − λ k + 1 ) ∑ i = 1 k λ i 1 − λ k + 1 f ( x i ) ( ② ) ≤ λ k + 1 f ( x k + 1 ) + ( 1 − λ k + 1 ) f ( ∑ i = 1 k λ i 1 − λ k + 1 x i ) ( ③ ) ≤ f ( λ k + 1 x k + 1 + ( 1 − λ k + 1 ) ∑ i = 1 k λ i 1 − λ k + 1 x i ) ( ④ ) = f ( λ k + 1 x k + 1 + ∑ i = 1 k λ i x i ) ( ⑤ ) = f ( ∑ i = 1 k + 1 λ i x i ) ( ⑥ ) \begin{aligned} \sum_{i=1}^{k+1}\lambda_i f(x_i)&=\lambda_{k+1}f(x_{k+1})+\sum_{i=1}^k\lambda_if(x_i) &\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space&{(①)} \\ &=\lambda_{k+1}f(x_{k+1})+(1-\lambda_{k+1})\sum_{i=1}^k\frac{\lambda_{i}}{1-\lambda_{k+1}}f(x_i) &&{(②)} \\ &\le \lambda_{k+1}f(x_{k+1})+(1-\lambda_{k+1})f\left(\sum_{i=1}^k\frac{\lambda_{i}}{1-\lambda_{k+1}}x_i\right) &&{(③)} \\ &\le f\left(\lambda_{k+1}x_{k+1}+(1-\lambda_{k+1})\sum_{i=1}^k\frac{\lambda_{i}}{1-\lambda_{k+1}}x_i\right) &&{(④)} \\ &=f\left( \lambda_{k+1}x_{k+1} + \sum_{i=1}^k\lambda_{i}x_i \right) &&{(⑤)} \\ &=f\left( \sum_{i=1}^{k+1} \lambda_i x_i \right) &&{(⑥)} \end{aligned} i=1∑k+1λif(xi)=λk+1f(xk+1)+i=1∑kλif(xi)=λk+1f(xk+1)+(1−λk+1)i=1∑k1−λk+1λif(xi)≤λk+1f(xk+1)+(1−λk+1)f(i=1∑k1−λk+1λixi)≤f(λk+1xk+1+(1−λk+1)i=1∑k1−λk+1λixi)=f(λk+1xk+1+i=1∑kλixi)=f(i=1∑k+1λixi) (①)(②)(③)(④)(⑤)(⑥)
因此,当 n = k + 1 n=k+1 n=k+1 时,不等式成立。
对上面推导的部分过程进行说明。
② → \to → ③:令 μ i = λ i 1 − λ k + 1 \mu_i=\frac{\lambda_i}{1-\lambda_{k+1}} μi=1−λk+1λi,满足 ∑ i = 1 k μ i = 1 \sum_{i=1}^k\mu_i=1 ∑i=1kμi=1,利用 Jensen 不等式可得 ∑ i = 1 k μ i f ( x i ) ≤ f ( ∑ i = 1 k μ i x i ) \sum_{i=1}^k \mu_{i}f(x_i)\le f(\sum_{i=1}^k \mu_i x_i) ∑i=1kμif(xi)≤f(∑i=1kμixi) ;
③ → \to → ④:令 y 1 = x k + 1 y_1=x_{k+1} y1=xk+1, y 2 = ∑ i = 1 k λ i 1 − λ k + 1 x i y_2=\sum_{i=1}^k\frac{\lambda_{i}}{1-\lambda_{k+1}}x_i y2=∑i=1k1−λk+1λixi,满足 λ k + 1 + ( 1 − λ k + 1 ) = 1 \lambda_{k+1} + (1-\lambda_{k+1})=1 λk+1+(1−λk+1)=1,利用 Jensen 不等式可得 λ k + 1 f ( y 1 ) + ( 1 − λ k + 1 ) f ( y 2 ) ≤ f ( λ k + 1 y 1 + ( 1 − λ k + 1 ) y 2 ) \lambda_{k+1}f(y_1) + (1-\lambda_{k+1})f(y_2)\le f(\lambda_{k+1}y_1+(1-\lambda_{k+1})y_2) λk+1f(y1)+(1−λk+1)f(y2)≤f(λk+1y1+(1−λk+1)y2) 。
故上凸函数的 Jensen 不等式成立。对于下凸函数的不等式证明同理。
EM 算法
概述
通过一个例子对 EM 算法进行介绍,以便于有整体、直观的认识。
(三硬币模型)假设有 3 3 3 枚硬币,分别记作 A \rm A A, B \rm B B, C \rm C C。这些硬币正面出现的概率分别是 π \rm \pi π, p p p 和 q q q。进行如下掷硬币试验:先掷硬币 A \rm A A,根据其结果选出硬币 B \rm B B 或硬币 C \rm C C,正面选硬币 B \rm B B,反面选硬币 C \rm C C;然后掷选出的硬币,掷硬币的结果,出现正面记作 1 1 1,出现反面记作 0 0 0;独立地重复 n n n 次试验(这里, n = 10 n = 10 n=10 ),观测结果如下
1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 1,1,0,1,0,0,1,0,1,1 1,1,0,1,0,0,1,0,1,1
假设只能观测到掷硬币的结果,不能观测掷硬币的过程。问如何估计三硬币正面出现的概率,即三硬币模型的参数。
对于这样一个问题,我们可以定义两个随机变量。随机变量 y y y 表示表示一次试验观测的结果是 1 1 1 或 0 0 0,称 y y y 为观测变量;随机变量 z z z 表示未观测到的掷硬币 A \rm A A 的结果,称 z z z 为隐变量; θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q) 是模型参数。这一模型是以上数据的生成模型。
注意,随机变量 y y y 的数据可以观测,随机变量 z z z 的数据不可观测。
在多组实验中,将观测数据表示为 Y = ( Y 1 , Y 2 , … , Y n ) T Y=(Y_1,Y_2,\dots,Y_n)^T Y=(Y1,Y2,…,Yn)T,未观测数据表示为 Z = ( Z 1 , Z 2 , … , Z n ) T Z=(Z_1,Z_2,\dots,Z_n)^T Z=(Z1,Z2,…,Zn)T。
下面给出一般的规定。用 Y Y Y 表示观测随机变量的数据, Z Z Z 表示隐随机变量的数据。 Y Y Y 和 Z Z Z 连在一起称为完全数据(complete-data),观测数据 Y Y Y 又称为不完全数据(incomplete-data)。假设给定观测数据 Y Y Y,其概率分布是 P ( Y ∣ θ ) P(Y\mid\theta) P(Y∣θ),其中 θ \theta θ 是需要估计的模型参数,那么不完全数据 Y Y Y 的似然函数是 P ( Y ∣ θ ) P(Y\mid \theta) P(Y∣θ),对数似然函数 L ( θ ) = log P ( Y ∣ θ ) L(\theta)= \log P(Y\mid\theta) L(θ)=logP(Y∣θ);假设 Y Y Y 和 Z Z Z 的联合概率分布是 P ( Y , Z ∣ θ ) P(Y,Z\mid\theta) P(Y,Z∣θ),那么完全数据的对数似然函数是 log P ( Y , Z ∣ θ ) \log P(Y,Z\mid \theta) logP(Y,Z∣θ)。
EM 算法通过迭代求 L ( θ ) L(\theta) L(θ) 的极大似然估计。每次迭代包含两步:E 步,求期望(我更喜欢称之为,更新隐变量);M 步,求极大化(我更喜欢称之为,更新模型参数)。EM 算法的过程可以大致描述为,利用第 i i i 次迭代得到的模型参数 θ \theta θ 的估计值 θ ( i ) \theta^{(i)} θ(i) 在第 i + 1 i+1 i+1 次迭代的 E 步计算完全数据的对数似然函数 log P ( Y , Z ∣ θ ) \log P(Y,Z\mid \theta) logP(Y,Z∣θ) 关于在给定观测数据 Y Y Y 和当前参数 θ ( i ) \theta^{(i)} θ(i) 下对未观测数据 Z Z Z 的条件概率分布 P ( Z ∣ Y , θ ( i ) ) P(Z\mid Y,\theta^{(i)}) P(Z∣Y,θ(i)) 的期望,即 Q ( θ , θ ( i ) ) = ∑ Z log P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) Q(\theta,\theta^{(i)})=\sum_Z\log P(Y,Z\mid \theta)P(Z\mid Y,\theta^{(i)}) Q(θ,θ(i))=∑ZlogP(Y,Z∣θ)P(Z∣Y,θ(i)) ;在 M 步中将使上面期望极大化的 θ \theta θ 确定为第 i + 1 i+1 i+1 次迭代的模型参数估计值 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),即 θ ( i + 1 ) = a r g max θ Q ( θ , θ ( i ) ) \theta^{(i+1)}={\rm arg}\space \max\limits_\theta Q(\theta,\theta^{(i)}) θ(i+1)=arg θmaxQ(θ,θ(i));不断进行 E 步和 M 步直至满足终止条件。
EM 算法的作用与 GD 算法(梯度下降算法)类似,都是用于确定模型参数的优化算法。
之所以我更喜欢分别称 E 步和 M 步为更新隐变量和更新模型参数,是因为在实际接触到的一些通过 EM 算法来优化的模型,其 E 步具体的实现就是在根据上一次 M 步的迭代所得的模型参数更新隐变量,其 M 步具体的实现为根据本次 E 步的迭代所得的隐变量更新模型参数,不断迭代直至满足停止条件。上面提到的期望,其实是对模型进行优化的目标函数,一般选取极大似然函数,所以需要让目标函数值随着迭代变大。
隐变量
讲到这里,EM 算法可以被总结为一种引入(或存在)隐变量的迭代算法。在最初没有接触任何模型时,初学者往往很难理解这种形式化的语言,下面我结合简单的例子通俗地介绍一下隐变量。
有时我们认为隐变量是本身就存在于模型当中的,有时是为了方便才为模型添加隐变量,总而言之,当隐变量的存在具有一定的合理性时,我们可以选择性地认为其存在或不存在于模型之中,当然,只有当引入隐变量能够便于计算或更贴近实际情况,我们才会引入隐变量,否则引入只会徒增模型复杂度。
以“三硬币模型”为例,我们知道该模型中的隐变量为“ 硬币 A \rm A A 投掷结果”,也就是以 A \rm A A 投掷的结果作为新的自变量,根据自变量取值选取硬币 B \rm B B 或 C \rm C C,投掷新选的硬币,投掷结果作为观测结果。为了便于理解,我们抽象地认为隐变量为“第二次投掷硬币”。不引入隐变量表示不进行第二次投掷,观测结果直接由投掷硬币 A \rm A A 决定;引入隐变量表示根据硬币 A \rm A A 的投掷结果选择不同的硬币再次投掷进而投掷结果作为观测结果。
这里引入的隐变量,即第二次投掷(选择哪个硬币),必须要依赖于硬币 A \rm A A 的投掷结果,否则,模型的观测结果将会与硬币 A \rm A A 完全无关, A \rm A A 就没有存在的必要了,这与我们要建立“硬币 A \rm A A 影响观测结果”模型的思想相违背。
这个模型体现了隐变量的引入具有选择性。若不引入隐变量(第二次投掷),那么模型参数为 θ = ( π ) \theta=(\pi) θ=(π),我们只需要根据观测结果 { 1 , 1 , 0 , 1 , 0 , 0 , 1 , 0 , 1 , 1 } \{1,1,0,1,0,0,1,0,1,1\} {1,1,0,1,0,0,1,0,1,1} 来确定 π \pi π,一般选用(对数)极大似然估计来确定参数,这 10 10 10 次实验对应的(极大化)目标函数为 π 6 ( 1 − π ) 4 \pi^6(1-\pi)^4 π6(1−π)4;若引入隐变量(第二次投掷),那么模型参数变为 θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q), 相当于认为观测结果并不由 A \rm A A 的结果直接决定,而是根据 A \rm A A 的结果进行新一轮投掷,再根据投掷结果确定观测结果,这 10 10 10 次实验对应的(极大化)目标函数为 [ π p + ( 1 − π ) q ] 6 [ π ( 1 − p ) + ( 1 − π ) ( 1 − q ) ] 4 [\pi p+(1-\pi)q]^6[\pi(1-p)+(1-\pi)(1-q)]^4 [πp+(1−π)q]6[π(1−p)+(1−π)(1−q)]4 。
注意,我们无法确定观测结果就是硬币 A \rm A A 掷出来的结果,可以理解为我们在完全漆黑的房间投掷硬币 A \rm A A,掷后离开房间,裁判进到房间观察硬币状况,进行一系列我们不知道的操作后,告诉我们他观测到的结果。可见,在这种理解的基础上,隐变量可以认为是我们对裁判暗箱操作的猜测,不引入隐变量就意味着我们认为裁判是秉持公平原则的,我们投掷出的硬币 A \rm A A 是什么情况,裁判就告诉我们什么情况。
通过一个更抽象的例子从直观上理解隐变量。有一个同事,有时候上班带伞有时候不带伞,当问他为什么带伞时,他会回到“因为今天是XX月XX日啊!”。因为我有点社恐,所以不好意思细问日期的含义,但是又非常想预测出他到底哪天会带伞哪天不会带伞。显然,直接根据日期去预测他是否带伞没有很好的解释性,“因为今天是6月1日,所以他带伞了”,这显然没有任何逻辑。于是,引入隐变量,认为根据日期可以确定季节,如果是夏天可能会因为晒或下雨带伞,其他天气或其他季节一般是不会带伞的。这样一来,不仅更好解释他带伞的原因,而且也提高了猜测的准确性。
接触过潜在语义分析(LSA)的同学知道,相比于朴素的词向量空间模型,潜在语义分析引入了“语义”作为隐变量。从网络模型的角度来看,语义的引入实现了降维,防止了模型过拟合,同时一定程度上减少了训练的参数量;从可解释性的角度来看,语义的引入比较优质地解决了朴素词向量空间模型无法处理一词多义、多词同义的问题。
算法模板
感觉在实践中并不会套用模板来训练模型参数,这里仅用来加深对 EM 算法理解。
输入:观测变量数据 Y Y Y,隐变量数据 Z Z Z,联合分布 P ( Y , Z ∣ θ ) P(Y,Z\mid \theta) P(Y,Z∣θ),条件分布 P ( Z ∣ Y , θ ) P(Z\mid Y,\theta) P(Z∣Y,θ);
输出:模型参数 θ \theta θ 。
(1)选择参数的初值 θ ( 0 ) \theta^{(0)} θ(0),开始迭代;
(2)E 步:记 θ ( i ) \theta^{(i)} θ(i) 为第 i i i 次迭代参数 θ \theta θ 的估计值,在第 i + 1 i+1 i+1 次迭代的 E 步,计算
Q ( θ , θ ( i ) ) = E Z [ log P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) (5) \begin{aligned} Q(\theta,\theta^{(i)})&=E_Z[\log P(Y,Z\mid \theta)\mid Y,\theta^{(i)}] \\ &=\sum_Z P(Z\mid Y,\theta^{(i)})\log P(Y,Z\mid \theta) \tag{5} \end{aligned} Q(θ,θ(i))=EZ[logP(Y,Z∣θ)∣Y,θ(i)]=Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ)(5)
其中, P ( Z ∣ Y , θ ( i ) ) P(Z\mid Y,\theta^{(i)}) P(Z∣Y,θ(i)) 是在给定观测数据 Y Y Y 和当前的参数估计 θ ( i ) \theta^{(i)} θ(i) 下隐变量数据 Z Z Z 的条件概率分布;
(3)M 步:求使 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i)) 极大化的 θ \theta θ,确定第 i + 1 i+1 i+1 次迭代的参数的估计值 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)
θ ( i + 1 ) = a r g max θ Q ( θ , θ ( i ) ) \theta^{(i+1)} ={\rm arg}\space \max_\theta Q(\theta, \theta^{(i)}) θ(i+1)=arg θmaxQ(θ,θ(i))
(4)重复第(2)步和第(3)步,直到收敛。
函数 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i)) 是 EM 算法的核心,其定义为,完全数据的对数似然函数 log P ( Y , Z ∣ θ ) \log P(Y,Z\mid \theta) logP(Y,Z∣θ) 关于在给定观测数据 Y Y Y 和当前参数 θ ( i ) \theta^{(i)} θ(i) 下对未观测数据 Z Z Z 的条件概率分布 P ( Z ∣ Y , θ ) P(Z\mid Y,\theta) P(Z∣Y,θ) 的期望称为 Q Q Q 函数,即式 ( 5 ) (5) (5) 。
对于上面 EM 算法模板的几点说明:
步骤(1):参数的初值可以任意选择,但需注意EM算法对初值是敏感的。
步骤(2):E 步求 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i)) 。 Q Q Q 函数式中 Z Z Z 是未观测数据, Y Y Y 是观测数据。注意, Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i)) 的第 1 1 1 个变元表示要极大化的参数,第 2 2 2 个变元表示参数的当前估计值。每次迭代实际在求 Q Q Q 函数及其极大。
步骤(3):M 步求 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i)) 的极大化,得到 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),完成一次迭代 θ ( i ) → θ ( i + 1 ) \theta^{(i)}\to \theta^{(i+1)} θ(i)→θ(i+1) 。后面将证明每次迭代使似然函数增大或达到局部极值。
步骤(4):给出停止迭代的条件,一般是对较小的正数 ε 1 \varepsilon_1 ε1, ε 2 \varepsilon_2 ε2,若满足
∣ ∣ θ ( i + 1 ) − θ ( i ) ∣ ∣ < ε 1 ||\theta^{(i+1)}-\theta^{(i)} ||\lt \varepsilon_1 ∣∣θ(i+1)−θ(i)∣∣<ε1
或
∣ ∣ Q ( θ ( i + 1 ) , θ ( i ) ) − Q ( θ ( i ) , θ ( i ) ) ∣ ∣ < ε 2 ||Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)}) ||\lt \varepsilon_2 ∣∣Q(θ(i+1),θ(i))−Q(θ(i),θ(i))∣∣<ε2
则停止迭代。
算法收敛性
下面会证明 EM 算法得到的 { θ ( i ) } \{\theta^{(i)}\} {θ(i)} 估计序列收敛,且收敛到全局最大值或局部极大值。
设 P ( Y ∣ θ ) P(Y\mid \theta) P(Y∣θ) 为观测数据的似然函数, θ ( i ) ( i = 1 , 2 , … ) \theta^{(i)}\space(i=1,2,\dots) θ(i) (i=1,2,…) 为 EM 算法得到的参数估计序列, P ( Y ∣ θ ( i ) ) ( i = 1 , 2 , … ) P(Y\mid \theta^{(i)})\space(i= 1,2,\dots) P(Y∣θ(i)) (i=1,2,…) 为对应的似然函数序列。接下来我们将证明 P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i)}) P(Y∣θ(i)) 单调递增,且存在上界,再根据“单调有界必有极限”的极限存在定理,我们很容易知道 P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i)}) P(Y∣θ(i)) 收敛到全局最大值或局部极大值。
因为 P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i)}) P(Y∣θ(i)) 为概率,所以显然存在上界。故下面主要证明其单调递增的性质。
证明 P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i)}) P(Y∣θ(i)) 是单调递增的,即证明 P ( Y ∣ θ ( i + 1 ) ) ≥ P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i+1)})\ge P(Y\mid \theta^{(i)}) P(Y∣θ(i+1))≥P(Y∣θ(i)) 。由于
P ( Y ∣ θ ) = P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ) P(Y\mid \theta)=\frac{P(Y,Z\mid \theta)}{P(Z\mid Y,\theta)} P(Y∣θ)=P(Z∣Y,θ)P(Y,Z∣θ)
取对数有
log P ( Y ∣ θ ) = log P ( Y , Z ∣ θ ) − log P ( Z ∣ Y , θ ) \log P(Y\mid \theta) =\log P(Y,Z\mid \theta)-\log P(Z\mid Y,\theta) logP(Y∣θ)=logP(Y,Z∣θ)−logP(Z∣Y,θ)
由式 ( 5 ) (5) (5)
Q ( θ , θ ( i ) ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) Q(\theta,\theta^{(i)})=\sum_ZP(Z\mid Y,\theta^{(i)})\log P(Y,Z\mid \theta) Q(θ,θ(i))=Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ)
令
H ( θ , θ ( i ) ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Z ∣ Y , θ ) (6) H(\theta, \theta^{(i)}) = \sum_ZP(Z\mid Y,\theta^{(i)})\log P(Z\mid Y,\theta)\tag{6} H(θ,θ(i))=Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ)(6)
于是对数似然函数可以写成
log P ( Y ∣ θ ) = Q ( θ , θ ( i ) ) − H ( θ , θ ( i ) ) (7) \log P(Y\mid \theta) = Q(\theta, \theta^{(i)}) - H(\theta, \theta^{(i)})\tag{7} logP(Y∣θ)=Q(θ,θ(i))−H(θ,θ(i))(7)
解释一下。
Q ( θ , θ ( i ) ) − H ( θ , θ ( i ) ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) − ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Z ∣ Y , θ ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ θ ) = log P ( Y ∣ θ ) \begin{aligned} Q(\theta, \theta^{(i)}) - H(\theta, \theta^{(i)}) &= \sum_Z P(Z\mid Y,\theta^{(i)})\log P(Y,Z\mid \theta)-\sum_ZP(Z\mid Y,\theta^{(i)})\log P(Z\mid Y,\theta) \\ &= \sum_Z P(Z\mid Y,\theta^{(i)}) \log \frac{P(Y,Z\mid \theta)}{P(Z\mid Y, \theta)} \\ &= \sum_Z P(Z\mid Y,\theta^{(i)}) \log P(Y\mid \theta) \\ &= \log P(Y\mid \theta) \end{aligned} Q(θ,θ(i))−H(θ,θ(i))=Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ)−Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ)=Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ)P(Y,Z∣θ)=Z∑P(Z∣Y,θ(i))logP(Y∣θ)=logP(Y∣θ)
其中,因为 ∑ Z P ( Z ∣ Y , θ ( i ) ) = 1 \sum_Z P(Z\mid Y,\theta^{(i)})=1 ∑ZP(Z∣Y,θ(i))=1,所以 ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ θ ) = log P ( Y ∣ θ ) \sum_Z P(Z\mid Y,\theta^{(i)}) \log P(Y\mid \theta)=\log P(Y\mid \theta) ∑ZP(Z∣Y,θ(i))logP(Y∣θ)=logP(Y∣θ) 。
在式 ( 7 ) (7) (7) 中分别取 θ \theta θ 为 θ ( i ) \theta^{(i)} θ(i) 和 θ ( i + 1 ) \theta^{(i+1)} θ(i+1) 并相减,有
log P ( Y ∣ θ ( i + 1 ) ) − log P ( Y ∣ θ ( i ) ) = [ Q ( θ ( i + 1 ) , θ ( i ) ) − Q ( θ ( i ) , θ ( i ) ) ] − [ H ( θ ( i + 1 ) , θ ( i ) ) − H ( θ ( i ) , θ ( i ) ) ] (8) \log P(Y\mid \theta^{(i+1)}) - \log P(Y\mid \theta^{(i)}) = [Q(\theta^{(i+1)},\theta^{(i)}) - Q(\theta^{(i)},\theta^{(i)})] - [H(\theta^{(i+1)},\theta^{(i)}) - H(\theta^{(i)},\theta^{(i)})]\tag{8} logP(Y∣θ(i+1))−logP(Y∣θ(i))=[Q(θ(i+1),θ(i))−Q(θ(i),θ(i))]−[H(θ(i+1),θ(i))−H(θ(i),θ(i))](8)
为证明 P ( Y ∣ θ ( i + 1 ) ) ≥ P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i+1)})\ge P(Y\mid \theta^{(i)}) P(Y∣θ(i+1))≥P(Y∣θ(i)),只需证式 ( 8 ) (8) (8) 右端是非负的。式 ( 8 ) (8) (8) 右端第一项,由于 θ ( i + 1 ) \theta^{(i+1)} θ(i+1) 使 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i)) 达到极大,所以有
Q ( θ ( i + 1 ) , θ ( i ) ) − Q ( θ ( i ) , θ ( i ) ) ≥ 0 (9) Q(\theta^{(i+1)},\theta^{(i)}) - Q(\theta^{(i)},\theta^{(i)})\ge 0\tag{9} Q(θ(i+1),θ(i))−Q(θ(i),θ(i))≥0(9)
其第二项,由式 ( 6 ) (6) (6) 可得
H ( θ ( i + 1 ) , θ ( i ) ) − H ( θ ( i ) , θ ( i ) ) = ∑ Z ( log P ( Z ∣ Y , θ ( i + 1 ) ) P ( Z ∣ Y , θ ( i ) ) ) P ( Z ∣ Y , θ ( i ) ) ≤ log ( ∑ Z P ( Z ∣ Y , θ ( i + 1 ) ) P ( Z ∣ Y , θ ( i ) ) P ( Z ∣ Y , θ ( i ) ) ) = log ( ∑ Z P ( Z ∣ Y , θ ( i + 1 ) ) ) = 0 (10) \begin{aligned} H(\theta^{(i+1)},\theta^{(i)}) - H(\theta^{(i)},\theta^{(i)}) &=\sum_Z\left( \log \frac{P(Z\mid Y,\theta^{(i+1)})}{P(Z\mid Y,\theta^{(i)})} \right) P(Z\mid Y, \theta^{(i)}) \\ &\le \log\left(\sum_Z \frac{P(Z\mid Y,\theta^{(i+1)})}{P(Z\mid Y,\theta^{(i)})} P(Z\mid Y, \theta^{(i)})\right) \\ &=\log \left( \sum_Z P(Z\mid Y,\theta^{(i+1)}) \right) = 0 \tag{10} \end{aligned} H(θ(i+1),θ(i))−H(θ(i),θ(i))=Z∑(logP(Z∣Y,θ(i))P(Z∣Y,θ(i+1)))P(Z∣Y,θ(i))≤log(Z∑P(Z∣Y,θ(i))P(Z∣Y,θ(i+1))P(Z∣Y,θ(i)))=log(Z∑P(Z∣Y,θ(i+1)))=0(10)
这里的不等号由 Jensen 不等式 ( 4 ) (4) (4) 得到。
由式 ( 9 ) (9) (9) 和式 ( 10 ) (10) (10) 可知式 ( 8 ) (8) (8) 右端是非负的,说明 P ( Y ∣ θ ( i + 1 ) ) ≥ P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i+1)})\ge P(Y\mid \theta^{(i)}) P(Y∣θ(i+1))≥P(Y∣θ(i)),即似然函数序列 P ( Y ∣ θ ( i ) ) P(Y\mid \theta^{(i)}) P(Y∣θ(i)) 单调递增。根据极限存在定理“单调有界必有极限”‘可知 EM 算法关于对数似然函数序列 L ( θ ( i ) ) L( \theta^{(i)}) L(θ(i)) 是收敛的,但是不能保证一定收敛到全局最大值,除非目标函数 L ( θ ) L(\theta) L(θ) 为上凸函数,这点与梯度下降法的迭代类似。
算法推导
上面介绍了 EM 算法。为什么 EM 算法能近似实现对观测数据的极大似然估计呢?下面通过近似求解观测数据的对数似然函数的极大化问题来导出 EM 算法,由此可以清楚地看出 EM 算法的作用。
我们面对一个含有隐变量的概率模型,目标是极大化观测数据(不完全数据) Y Y Y 关于参数 θ \theta θ 的对数似然函数,即极大化
L ( θ ) = log P ( Y ∣ θ ) = log ∑ Z P ( Y , Z ∣ θ ) (11) \begin{aligned} L(\theta)&=\log P(Y\mid \theta) \\ &=\log \sum_Z P(Y,Z\mid \theta)\tag{11} \end{aligned} L(θ)=logP(Y∣θ)=logZ∑P(Y,Z∣θ)(11)
也可以写成积分形式,下同。
※ 当只有一组数据时,对数似然函数如式 ( 11 ) (11) (11) 所示;当有多组数据时,全部数据的对数似然函数应该定义为每组数据的对数似然函数之和,即
L ( θ ) = ∑ i = 1 N log P ( Y i ∣ θ ) L(\theta)=\sum_{i=1}^N\log P(Y_i\mid \theta) L(θ)=i=1∑NlogP(Yi∣θ)
其中,总共 N N N 组数据, Y i Y_i Yi 表示第 i i i 组数据的观测数据。
EM 算法是通过迭代逐步近似极大化 L ( θ ) L(\theta) L(θ) 的。假设在第 i i i 次迭代后 θ \theta θ 的估计值是 θ ( i ) \theta^{(i)} θ(i)。我们希望新估计值 θ \theta θ 能使 L ( θ ) L(\theta) L(θ) 增加,即 L ( θ ) > L ( θ ( i ) ) L(\theta)>L(\theta^{(i)}) L(θ)>L(θ(i)),并逐步达到极大值。为此,考虑两者的差
L ( θ ) − L ( θ ( i ) ) = log ∑ Z P ( Y , Z ∣ θ ) − log P ( Y ∣ θ ( i ) ) L(\theta)-L(\theta^{(i)}) = \log \sum_Z P(Y,Z\mid \theta) - \log P(Y\mid \theta^{(i)}) L(θ)−L(θ(i))=logZ∑P(Y,Z∣θ)−logP(Y∣θ(i))
利用 Jensen 不等式得到其下界
L ( θ ) − L ( θ ( i ) ) = log ( ∑ Z q ( Z , θ ( i ) ) P ( Y , Z ∣ θ ) q ( Z , θ ( i ) ) ) − log P ( Y ∣ θ ( i ) ) ( ① ) ≥ ∑ Z q ( Z , θ ( i ) ) log P ( Y , Z ∣ θ ) q ( Z , θ ( i ) ) − log P ( Y ∣ θ ( i ) ) ( ② ) = ∑ Z q ( Z , θ ( i ) ) log P ( Y , Z ∣ θ ) q ( Z , θ ( i ) ) − ∑ Z q ( Z , θ ( i ) ) log P ( Y ∣ θ ( i ) ) ( ③ ) = ∑ Z q ( Z , θ ( i ) ) log P ( Y , Z ∣ θ ) q ( Z , θ ( i ) ) P ( Y ∣ θ ( i ) ) ( ④ ) \begin{aligned} L(\theta)-L(\theta^{(i)}) &= \log \left( \sum_Z q(Z,\theta^{(i)})\frac{P(Y,Z\mid \theta)}{q(Z,\theta^{(i)})} \right) - \log P(Y\mid \theta^{(i)}) &\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space&{(①)} \\ &\ge \sum_Z q(Z,\theta^{(i)}) \log \frac{P(Y,Z\mid \theta)}{q(Z,\theta^{(i)})} - \log P(Y\mid \theta^{(i)}) &&{(②)} \\ &= \sum_Z q(Z,\theta^{(i)}) \log \frac{P(Y,Z\mid \theta)}{q(Z,\theta^{(i)})} - \sum_Z q(Z,\theta^{(i)})\log P(Y\mid \theta^{(i)}) &&{(③)} \\ &=\sum_Z q(Z,\theta^{(i)}) \log \frac{P(Y,Z\mid \theta)}{q(Z,\theta^{(i)})P(Y\mid \theta^{(i)})} &&{(④)} \end{aligned} L(θ)−L(θ(i))=log(Z∑q(Z,θ(i))q(Z,θ(i))P(Y,Z∣θ))−logP(Y∣θ(i))≥Z∑q(Z,θ(i))logq(Z,θ(i))P(Y,Z∣θ)−logP(Y∣θ(i))=Z∑q(Z,θ(i))logq(Z,θ(i))P(Y,Z∣θ)−Z∑q(Z,θ(i))logP(Y∣θ(i))=Z∑q(Z,θ(i))logq(Z,θ(i))P(Y∣θ(i))P(Y,Z∣θ) (①)(②)(③)(④)
对上面推导的部分过程进行说明。
①:引入关于 Z Z Z 的分布 q ( Z , θ ) q(Z,\theta) q(Z,θ),在已知 θ \theta θ 为 θ ( i ) \theta^{(i)} θ(i) 的前提下,分布 q ( Z , θ ( i ) ) q(Z,\theta^{(i)}) q(Z,θ(i)) 是已知的,满足 ∑ Z q ( Z , θ ( i ) ) = 1 \sum_Z q(Z,\theta^{(i)})=1 ∑Zq(Z,θ(i))=1 ;
① → \to → ②:由于 log ( ⋅ ) \log(·) log(⋅) 函数为上凸函数,故可用 Jensen 不等式 ( 4 ) (4) (4) ;
③:第二项添加中 q ( Z , θ ( i ) ) q(Z,\theta^{(i)}) q(Z,θ(i)),同时保证与 ② 相等;
④:对数函数运算法则,两个对数函数的减法等于自变量相除取对数。
令
B ( θ , θ ( i ) ) = L ( θ ( i ) ) + ∑ Z q ( Z , θ ( i ) ) log P ( Y , Z ∣ θ ) q ( Z , θ ( i ) ) P ( Y ∣ θ ( i ) ) (12) B(\theta,\theta^{(i)})=L(\theta^{(i)})+\sum_Z q(Z,\theta^{(i)})\log \frac{P(Y,Z\mid \theta)}{q(Z,\theta^{(i)})P(Y\mid \theta^{(i)})} \tag{12} B(θ,θ(i))=L(θ(i))+Z∑q(Z,θ(i))logq(Z,θ(i))P(Y∣θ(i))P(Y,Z∣θ)(12)
则
L ( θ ) ≥ B ( θ , θ ( i ) ) L(\theta)\ge B(\theta,\theta^{(i)}) L(θ)≥B(θ,θ(i))
即函数 B ( θ , θ ( i ) ) B(\theta, \theta^{(i)}) B(θ,θ(i)) 是 L ( θ ) L(\theta) L(θ) 的一个下界。
选取的分布 q ( Z , θ ( i ) ) q(Z,\theta^{(i)}) q(Z,θ(i)) 应该保证下界 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)) 尽可能逼近对数似然函数 L ( θ ) L(\theta) L(θ),当上面的 Jensen 不等式 ② 等号成立时,下界与对数似然函数(之差)完全相等,等号成立时的 q q q 函数显然是理论上的最优解。
上面的 Jensen 不等式 ② 中的 f ( ⋅ ) = log ( ⋅ ) f(·)=\log(·) f(⋅)=log(⋅),此时 f ( ⋅ ) f(·) f(⋅) 已经确定为上凸函数,那么只能让 ⋅ = C ( C 为 常 数 ) ·=C\space(C为常数) ⋅=C (C为常数) 以保证 f ( ⋅ ) = log ( C ) = C ′ ( C ′ 为 常 数 ) f(·)=\log(C)=C'\space(C'为常数) f(⋅)=log(C)=C′ (C′为常数),此时 f ( ⋅ ) = log ( C ) f(·)=\log(C) f(⋅)=log(C) 为线性函数,根据上面讨论的等号成立条件可知,只有当 ② 中的 P ( Y , Z ∣ θ ) q ( Z , θ ( i ) ) = C \frac{P(Y,Z\mid \theta)}{q(Z,\theta^{(i)})}=C q(Z,θ(i))P(Y,Z∣θ)=C 时,等号成立。
为了推导的方便,不妨将模型参数暂时忽略。即已知 C q ( Z ) = P ( Y , Z ) Cq(Z)=P(Y,Z) Cq(Z)=P(Y,Z),两侧同时求期望(或积分)得
C q ( Z ) = P ( Y , Z ) C ∑ Z q ( Z ) = P ( Y ) C = P ( Y ) \begin{aligned} Cq(Z)&=P(Y,Z) \\ C\sum_Zq(Z)&=P(Y) \\ C&=P(Y) \end{aligned} Cq(Z)CZ∑q(Z)C=P(Y,Z)=P(Y)=P(Y)
将 C = P ( Y ) C=P(Y) C=P(Y) 代回 C q ( Z ) = P ( Y , Z ) Cq(Z)=P(Y,Z) Cq(Z)=P(Y,Z) 得
q ( Z ) = P ( Y , Z ) P ( Y ) = P ( Z ∣ Y ) q(Z)=\frac{P(Y,Z)}{P(Y)}=P(Z\mid Y) q(Z)=P(Y)P(Y,Z)=P(Z∣Y)
因此
q ( Z , θ ) = P ( Z ∣ Y , θ ) (13) q(Z,\theta) = P(Z\mid Y,\theta) \tag{13} q(Z,θ)=P(Z∣Y,θ)(13)
因为我们希望在已知上一次迭代的模型参数 θ ( i ) \theta^{(i)} θ(i) 时,函数 q q q 为关于 Z Z Z 的分布是已知的,所以 ② 中 q q q 的参数为 θ ( i ) \theta^{(i)} θ(i) 而不是 θ \theta θ 。
当 ① 和 ② 中 q ( Z , θ ( i ) ) q(Z,\theta^{(i)}) q(Z,θ(i)) 表示为 q ( Z , θ ) q(Z,\theta) q(Z,θ) 时才能保证等号成立,所以有人可能疑惑,为什么 q ( Z , θ ( i ) ) q(Z,\theta^{(i)}) q(Z,θ(i)) 依然可行?
确实只有取 q ( Z , θ ) q(Z,\theta) q(Z,θ) 时等号才成立,即取在模型参数 θ \theta θ (或 θ ( i + 1 ) \theta^{(i+1)} θ(i+1))下的条件概率分布,而不是在模型参数 θ ( i ) \theta^{(i)} θ(i) 下的条件概率分布;但是我们是想通过 Jensen 不等式确定一个尽可能逼近对数似然函数的函数,并不是找到一个与之相同的函数,这样完全没意义,因为问题没有得到转化,所以我们退而求其次,认为第 i i i 次迭代得到的模型参数 θ ( i ) \theta^{(i)} θ(i) 下的条件概率分布与在模型参数 θ \theta θ (或 θ ( i + 1 ) \theta^{(i+1)} θ(i+1))下的条件概率分布效果相近,因此选用了 q ( Z , θ ( i ) ) q(Z,\theta^{(i)}) q(Z,θ(i)) 。当然,你也可以尝试选用 q ( Z , θ ( i − 1 ) ) = P ( Z ∣ Y , θ ( i − 1 ) ) q(Z,\theta^{(i-1)})=P(Z\mid Y,\theta^{(i-1)}) q(Z,θ(i−1))=P(Z∣Y,θ(i−1)) 。
更大可不必担心取 θ ( i ) \theta^{(i)} θ(i) 会不会使得 Jensen 不等式不再成立,Jensen 不等式的成立与具体的 q q q 函数无关,或者说 q q q 函数有多种取法,只要满足 Jensen 不等式的前提条件和 ∑ Z q ( Z ) = 1 \sum_Z q(Z)=1 ∑Zq(Z)=1 ,Jensen 不等式就必然成立。简单思考便可得知。
将 q ( Z , θ ( i ) ) = P ( Z ∣ Y , θ ( i ) ) q(Z,\theta^{(i)})=P(Z\mid Y,\theta^{(i)}) q(Z,θ(i))=P(Z∣Y,θ(i)) 代入到式 ( 12 ) (12) (12) 中得
B ( θ , θ ( i ) ) = L ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ θ ( i ) ) = L ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) P ( Y , Z ∣ θ ( i ) ) (14) \begin{aligned} B(\theta,\theta^{(i)})&=L(\theta^{(i)})+\sum_Z P(Z\mid Y,\theta^{(i)})\log \frac{P(Y,Z\mid \theta)}{P(Z\mid Y,\theta^{(i)})P(Y\mid \theta^{(i)})} \\ &=L(\theta^{(i)}) + \sum_Z P(Z\mid Y,\theta^{(i)})\log \frac{P(Y,Z\mid \theta)}{P(Y,Z\mid \theta^{(i)})} \tag{14} \end{aligned} B(θ,θ(i))=L(θ(i))+Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y,Z∣θ)=L(θ(i))+Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ(i))P(Y,Z∣θ)(14)
由式 ( 14 ) (14) (14) 可知
L ( θ ( i ) ) = B ( θ ( i ) , θ ( i ) ) (15) L(\theta^{(i)})=B(\theta^{(i)},\theta^{(i)}) \tag{15} L(θ(i))=B(θ(i),θ(i))(15)
因此,任何可以使 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)) 增大的 θ \theta θ,也可以使 L ( θ ) L(\theta) L(θ) 增大。为了使 L ( θ ) L(\theta) L(θ) 有尽可能大的增长,选择 θ ( i + 1 ) \theta^{(i+1)} θ(i+1) 使 B ( θ , θ ( i + 1 ) ) B(\theta,\theta^{(i+1)}) B(θ,θ(i+1)) 达到极大,即
θ ( i + 1 ) = a r g max θ B ( θ , θ ( i ) ) (16) \theta^{(i+1)}={\rm arg}\max_\theta B(\theta,\theta^{(i)})\tag{16} θ(i+1)=argθmaxB(θ,θ(i))(16)
解释一下“任何可以使 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)) 增大的 θ \theta θ,也可以使 L ( θ ) L(\theta) L(θ) 增大”。这句话的形式化表示为,当 B ( θ ( i + 1 ) , θ ( i ) ) > B ( θ ( i ) , θ ( i ) ) B(\theta^{(i+1)},\theta^{(i)})\gt B(\theta^{(i)},\theta^{(i)}) B(θ(i+1),θ(i))>B(θ(i),θ(i)) 时 L ( θ ( i + 1 ) ) > L ( θ ( i ) ) L(\theta^{(i+1)})\gt L(\theta^{(i)}) L(θ(i+1))>L(θ(i)) 。
简单证明, B ( θ ( i + 1 ) , θ ( i ) ) B(\theta^{(i+1)},\theta^{(i)}) B(θ(i+1),θ(i)) 作为 L ( θ ( i + 1 ) ) L(\theta^{(i+1)}) L(θ(i+1)) 的下界,满足 L ( θ ( i + 1 ) ) ≥ B ( θ ( i + 1 ) , θ ( i ) ) L(\theta^{(i+1)})\ge B(\theta^{(i+1)},\theta^{(i)}) L(θ(i+1))≥B(θ(i+1),θ(i)),根据式 ( 15 ) (15) (15) 知 B ( θ ( i ) , θ ( i ) ) = L ( θ ( i ) ) B(\theta^{(i)},\theta^{(i)})=L(\theta^{(i)}) B(θ(i),θ(i))=L(θ(i)),当 B ( θ ( i + 1 ) , θ ( i ) ) > B ( θ ( i ) , θ ( i ) ) B(\theta^{(i+1)},\theta^{(i)})\gt B(\theta^{(i)},\theta^{(i)}) B(θ(i+1),θ(i))>B(θ(i),θ(i)) 时,有
L ( θ ( i + 1 ) ) ≥ B ( θ ( i + 1 ) , θ ( i ) ) > B ( θ ( i ) , θ ( i ) ) = L ( θ ( i ) ) L(\theta^{(i+1)})\ge B(\theta^{(i+1)},\theta^{(i)})\gt B(\theta^{(i)},\theta^{(i)})=L(\theta^{(i)}) L(θ(i+1))≥B(θ(i+1),θ(i))>B(θ(i),θ(i))=L(θ(i))
证毕。
现在求 θ ( i + 1 ) \theta^{(i+1)} θ(i+1) 的表达式。求函数极大值对应的模型参数 θ \theta θ 可以忽略对 θ \theta θ 的极大化而言为常数的项。将式 ( 14 ) (14) (14) 代入式 ( 16 ) (16) (16) 得
θ ( i + 1 ) = a r g max θ ( L ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) P ( Y , Z ∣ θ ( i ) ) ) = a r g max θ ( L ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) − ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ( i ) ) ) = a r g max θ ( ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y , Z ∣ θ ) ) \begin{aligned} \theta^{(i+1)}&={\rm arg}\max_\theta\left( L(\theta^{(i)}) + \sum_Z P(Z\mid Y,\theta^{(i)})\log \frac{P(Y,Z\mid \theta)}{P(Y,Z\mid \theta^{(i)})} \right) \\ &={\rm arg}\max_\theta\left( L(\theta^{(i)}) + \sum_Z P(Z\mid Y,\theta^{(i)})\log P(Y,Z\mid \theta) - \sum_Z P(Z\mid Y,\theta^{(i)})\log P(Y,Z\mid \theta^{(i)}) \right) \\ &={\rm arg}\max_\theta\left(\sum_Z P(Z\mid Y,\theta^{(i)})\log P(Y,Z\mid \theta) \right)\\ \end{aligned} θ(i+1)=argθmax(L(θ(i))+Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ(i))P(Y,Z∣θ))=argθmax(L(θ(i))+Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ)−Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ(i)))=argθmax(Z∑P(Z∣Y,θ(i))logP(Y,Z∣θ))
第二个等式中的第一项和第三项均与 θ \theta θ 无关,可以认为是常数项,所以可以忽略。
如果还是不能理解,我们以求偏导的规则来理解,若对 θ \theta θ 求偏导,则第一项和第三项显然相当于常数,对偏导没有贡献,但是第二项不同。
根据式 ( 5 ) (5) (5) 可知
θ ( i + 1 ) = a r g max θ Q ( θ , θ ( i ) ) (17) \theta^{(i+1)} = {\rm arg}\max_\theta Q(\theta, \theta^{(i)})\tag{17} θ(i+1)=argθmaxQ(θ,θ(i))(17)
式 ( 17 ) (17) (17) 等价于 EM 算法的一次迭代,即求 Q Q Q 函数及其极大化。EM 算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法。
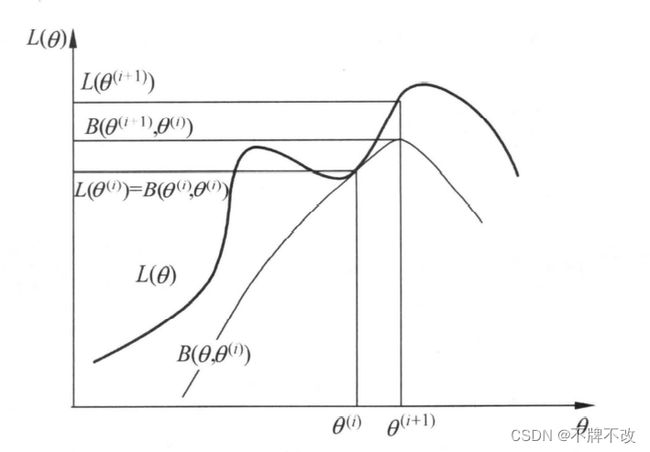
图 2 2 2 给出 EM 算法的直观解释。图中上方曲线为 L ( θ ) L(\theta) L(θ),下方曲线为 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i))。 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)) 为对数似然函数 L ( θ ) L(\theta) L(θ) 的下界。由式 ( 15 ) (15) (15),两个函数在点 θ = θ ( i ) \theta=\theta^{(i)} θ=θ(i) 处相等。由式 ( 16 ) (16) (16) 和式 ( 17 ) (17) (17),EM算法找到下一个点 θ ( i + 1 ) \theta^{(i+1)} θ(i+1) 使函数 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)) 极大化。这时由于 L ( θ ) ≥ B ( θ , θ ( i ) ) L(\theta)\ge B(\theta,\theta^{(i)}) L(θ)≥B(θ,θ(i)),函数 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)) 的增加,保证对数似然函数 L ( θ ) L(\theta) L(θ) 在每次迭代中也是增加的。
之所以 EM 算法可以将最大化 B B B 转换为最大化 Q Q Q,通过对比式 ( 14 ) (14) (14) 和式 ( 5 ) (5) (5) 可以发现,二者仅相差一个与 θ \theta θ 无关的常数,并不影响最大化对应的解,因此 EM 算法采用最大化形式更为简洁的 Q Q Q 函数。EM 算法在点 θ ( i + 1 ) \theta^{(i+1)} θ(i+1) 重新计算 Q Q Q 函数值,进行下一次迭代。在这个过程中,对数似然函数 L ( θ ) L(\theta) L(θ) 不断增大。从图可以推断出 EM 算法不能保证找到全局最优值。
图 2 EM 算法的解释
适用场景
在学习模型参数时,极大似然函数是比较受青睐的一种定义目标函数的方式。
当目标函数比较简单时,可以通过目标函数对每个参数求偏导,并令导数为零计算出解析解。多解时可以对尝试使用每个模型参数计算似然函数,取最大值对应的模型参数作为最优解;
但是模型通常比较复杂,计算出来的导函数(方程组)难以求解。此时,可以仅计算出导函数值,通过梯度下降的方法,使参数向梯度下降最快的方向移动一小步来更新参数;
更有甚者,连目标函数的导函数(方程组)都难以获得,比如一些概率生成模型或者单纯导数计算困难的模型等。对于这些不可直接求导的模型,需要引入隐变量,采用 EM 算法来简化计算。当然,如果向模型中引入隐变量,那么必然要选择 EM 算法。
EM 算法与 GD 算法
以下是我自己的片面理解,网上可借鉴的资料比较少,希望大家辩证地来看。
EM 算法和 GD 算法计算出来的往往是局部最优解且为数值解。
EM 算法常用于概率模型,而概率模型一般有对应的生成模型;EM 算法更能体现数学之美,不像梯度下降法一样重复地计算导函数值进行更新,而是利用概率论相关知识进行化简、抽象,进而获得 E 步和 M 步的计算;EM 算法与坐标下降法类似,两次(或多次)计算作为一次迭代,且均为非梯度化优化算法。
GD 算法常用于深度网络模型中,主要是因为在深度网络模型中,我们选取的激活函数一般都可导,这是梯度下降法可以大展身手的原因之一;梯度下降法更加直观易懂,其原理就是沿着梯度下降最快的方向移动,保证目标函数值减小(步长合适时)。
参考
[1] 《统计学习方法(第二版)》李航著
[2] 琴生不等式 - 百度百科
[3] Jensen不等式讲解与证明 - CSDN博客
[4] EM 算法的收敛性证明 - CSDN博客
[5] 机器学习-EM算法3(公式导出之ELBO+Jensen Inequlity)- bilibili
[6] 梯度下降与EM算法 - CSDN博客