《深度卷积神经网络原理与实践》笔记 第二、三章 卷积神经网络原理及典型结构

本笔记是依据周浦城等教授编著的《深度卷积神经网络原理与实践》的个人笔记（Version：1.0.0）

整理作者：sq_csl

第二、三章 卷积神经网络原理及典型结构

1.1卷积神经网络概述

1.1.1 卷积神经网络的发展

卷积神经网络的发展大体上经历了三个阶段，即：
理论提出阶段：卷积神经网络的发展最早可追溯到20世纪60年代。
模型实现阶段：1989年，Y. LeCun等人提出了最初的卷积神经网络模型。
广泛研究阶段：（目前）卷积神经网络已经广泛应用于目标检测、视频分类、人脸识别、行人验证、行为识别、姿态估计、语义分割、人群密度估计、图像质量评价等诸多领域。

1.1.2 卷积神经网络的基本原理及组成

卷积神经网络的本质是映射。例如：
一个用于目标分类的卷积神经网络，实现了从图像到类别的映射。
一个用于目标检测的网络，实现了从图像到类别和空间位置信息的映射。
一个风格迁移（style transfer）网络，实现了从图像到艺术风格化的映射。

有四个基本层：卷积层(Convolutional Layer)、激活层(Activation Layer)、池化层(Pooling Layer)和全连接层(Fully Connected Layer)。

1.2 卷积层（Convolution Layer）

1.2.1 基本的卷积（convolution）运算

信号的卷积：卷积（convolution）是信号分析与处理中一种重要的运算，表征了函数$x$与$h$经过翻转和平移的重叠部分函数值乘积对重叠长度的积分，式子中“$\ast$”代表卷积运算，连续信号形式为：

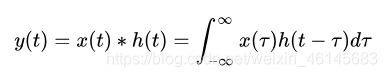
其离散信号形式为：

图像的卷积：在图像处理中，参与卷积的两个信号一个称为输入图像，另一个称为卷积核（又叫滤波器，filter）。与一般信号卷积相比，图像的卷积有两点不同：一是运算时并不对信号进行翻转（因此实际上是一种互相关运算）；二是只对卷积核与输入图像完全重叠的部分进行运算。

1.2.2 卷积神经网络中的卷积运算

单通道卷积运算： 设输入为二维矩阵I，卷积核K的大小为m×n，则:
其中，输出图像$S(i,j)$成为特征图(feature map)；卷积核$K$中的元素称为权值(weight),$b$称为偏置(bias)。另外，卷积核每次在输入图像上的像素数$s$称为步长。
注：卷积层的前向传播过程可用多层感知机模型来表述；实现的是局部的不完全连接；每组连接的权值相同，称为权值共享(weight sharing)。（优势：使得CNN可以大幅减少网络参数，提高网络效率）

多通道卷积运算： 假设输入数据有c个通道，首先将卷积核的每个通道分别与相应的输入数据通道进行卷积，然后将得到的特征图对应元素相加，最终输出一个单通道的特征图，其数学表达式为：
$S(i,j)=\left({\sum }_c(I_c\ast K_c)(i,j)\right)$

填充操作： 为了减少卷积时造成的信息损失（图像尺寸越来越小），一般通过在图像的外围填充一部分人为构建的像素，使得卷积核中心可以到达原始输入图像上的每一个坐标，从而输出完整的特征图。

填充的宽度p由具体应用决定，根据填充的数据的选择，可以将操作分为以下三种：零填充（填充的数据均为0）、重复填充（填充数据是距离当前位置最近的像素的原始数据）、常数填充（填充的数据均为指定值）

1.2.3 卷积的作用

在数字图像处理中，利用卷积运算不仅可以用于图像去噪、增强等问题，还可以用于提取图像的边缘、角点、线段等几何特征。在卷积神经网络中，卷积层主要用来对图像的某些二维视觉特征产生响应。卷积核的权重，决定了网络对什么样的特征进行响应。
在卷积神经网络中，卷积核的权重与偏置是待学习的参数。通过在数据集上的训练，卷积神经网络最终能够学习出最适合表达图像特征的一组卷积核。

1.2.4 卷积层及参数

在卷积神经网络中对输入数据实现卷积计算的单元叫做卷积层。卷积层包含了一个或多个尺寸相等的卷积核，并利用这些卷积核分别对输入数据进行卷积，得到多个特征图。由于一张图像或者一个目标可能会包含大量的特征，因此使用单个或者少量的卷积核去提取和描述目标是不现实的。一般实际应用时，网络一般包含多个卷积层，而且每个卷积层也包含多个甚至大量卷积核，用来提取目标不同的特征。

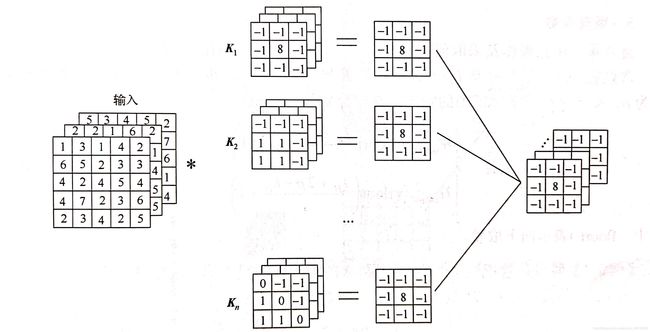
在实际中，卷积层的卷积核权重以及偏置是可学习的参数，最终通过网络训练来学习出最优的参数。卷积层的关键参数如下：

卷积核的通道数

一般等于输入数据的通道数。卷积核的各通道只和输入数据的对应通道进行卷积计算。

卷积核的尺寸

卷积核$K$的尺寸决定了参与运算的权值数量和感受野的大小。（但实际上通过池化操作，尺寸较小的卷积核也可以通过参数积累来获得更大的感受野）

卷积核的个数

一个卷积核对应输入图像上的某一个特征。

步长

进行卷积运算时，卷积核在输入数据上移动的步长$s$会影响特征图的尺寸。步长$s$即不能太大也不能太小。

填充参数

填充参数会影响特征图的尺寸。（原因见“填充操作”）
假设输入图像的尺寸是$I_W\times I_H$，卷积核$K$尺寸为$k_W\times k_H$，步长为$s$,填充操作的填充宽度为$p$,则卷积结果即特征图的宽度和高度分别为：
$W_o=floor((I_W+2p-k_W)/s+1)$ $,$ $H_o=floor((I_H+2p-k_H)/s+1)$

1.2.5 特殊卷积

1×1 卷积

1×1卷积的卷积核尺寸为1×1像素。这种特殊的卷积核并不能提取空间几何特征。

空洞卷积

在卷积核各权值之间插入不参与运算的“空洞”。

全局卷积

如果将卷积核尺寸设置为与输入数据尺寸相同，则卷积得到的结果为一个1×1的标量。

反卷积

将最终的特征图放大到原始图像的尺寸，这种操作叫反卷积（transposed convolution），也叫转置卷积。

1.3 激活层

1.3.1 激活函数相关知识

梯度爆炸/消失问题

卷积神经网络是利用反向传播算法来实现参数更新的，其原理是根据复合函数求导的链式法则来实现梯度的传递。

激活函数的饱和性

假设$h(x)$是一个激活函数，对于其导数而言，当x趋近于正无穷时，函数的导数趋近于零，我们称其为右饱和；同理，当x趋近于负无穷时，函数的导数趋近于零，称其为左饱和。若一个函数既满足左饱和又满足右饱和，则该函数为饱和，典型的有sigmoid、Tanh函数。

硬饱和：

对于任意的x。若存在常数c，当x>c时，恒有$h^{\prime }(x)=0$成立，则称其为右硬饱和。同理，若存在常数c，当x$h^{\prime }(x)=0$成立，则称其为左硬饱和。当一个函数既满足又硬饱和和左硬饱和，则称该函数为硬饱和。

软饱和：

对于任意的x。若存在常数c，当x>c时，恒有$h^{\prime }(x)➡0$，则称其为右软饱和。同理，若存在常数c，当x$h^{\prime }(x)➡0$，则称其为左软饱和。当一个函数既满足右软饱和和左软饱和，则称该函数为软饱和。

激活函数的一般要求

非线性、良好的可导性、计算简单等。

1.3.2 典型的激活函数

Sigmoid 函数

Sigmoid具有指数函数的形状，在物理上最接近神经元。它的输出范围在0~1之间，可表示成概率或者用于数据的归一化。
缺点:容易产生梯度消失的问题、计算量较大、输出不是零均值。

Tanh函数

缺点：仍然会存在梯度消失的问题，计算量较大

ReLU函数

相比于Sigmoid和Tanh，它在x>0的时候，不存在饱和问题，从而使得梯度不会保持一直衰减，梯度消失问题也得到解决。
缺点：存在神经元“坏死”问题。也成为“ReLU死区”(Dying ReLU)问题（不合适的权值初始化和过大的学习率）；不是零均值的。

ReLU-Like 函数

针对ReLU函数存在的神经元“坏死”的问题，研究人员设计了许多改进方法，这些方法主要集中将$x<0$的部分进行处理。
Leaky ReLU
PReLU
RReLU
ELU

1.4 池化层

1.4.1 池化操作

池化层（Pooling Layer）对输入的数据进行池化操作，缩减数据的尺寸，同时尽可能的保留数据信息。池化的本质是数据压缩，一方面抑制响应较低的信号，降低噪声，另一方面减少需要学习的参数，降低网络规模，在空间上也实现了感受野的增大，有利于使用较小的卷积核实现更大尺度上的特征学习。

主要参数：池化核、池化步长

假设输入大小为i, 输出大小为o, 核大小(kernel size)简称k, 步长(stride)简称s，满足以下公式：$o=\lfloor (i-k)/s\rfloor +1$

池化层参数为超参数，不参与学习。目前最常见的池化核尺寸和池化步长都是2，为非重叠池化(no-overlapping Pooling)。常见池化方法主要为最大池化和平均池化等。

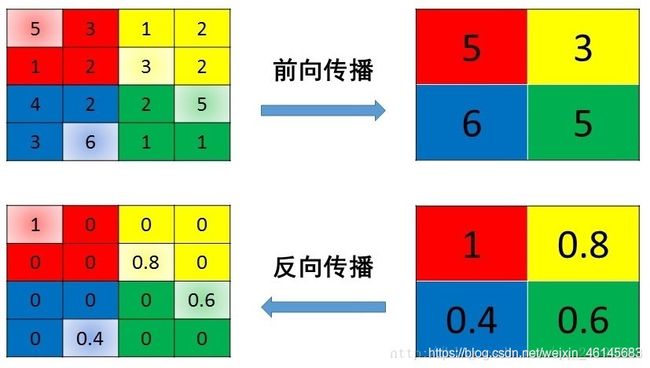
最大池化

最大池化过程类似于卷积过程，就是选择图像区域中最大值作为该区域池化以后的值，反向传播的时候，梯度通过前向传播过程的最大值反向传播，其他位置梯度为0。

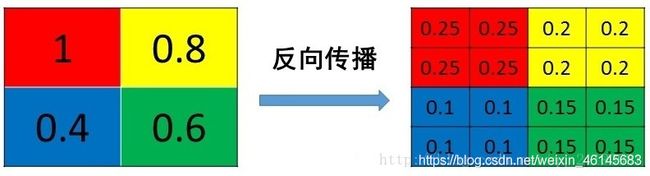
平均池化

平均池化就是将选择的图像区域中的平均值作为该区域池化以后的值。

1.4.2感受野

感受野原指听觉、视觉等神经系统中一些神经元的特性，即神经元只接受其所支配的刺激区域内的信号。
在卷积神经网络中，感受野是网络中每一层输出的特征图上的像素在输入图像上映射的区域大小。

如图所示的卷积神经网络，共3层，第一层为原始图像，卷积核中的每个像素对应于原始图像上的一个像素，能覆盖3×3区域，因此感受野为3×3；经过池化之后，第二层网络的输入图像中每个像素对应的是原始图像中2×2区域，如果用3×3的卷积核在原始图像为2×2的区域上去卷积，则覆盖的尺寸为7×7，因此第二层卷积核的感受野为7×7。（池化层增大了感受野）

1.5 全连接层

全连接层一般在网络的最后部分，其作用就是将二维的特征信息转化为一维的分类信息。全连接层的有m个输入和n个输出，每个输出都和所有的输入相连，相连的权重$w$都是不一样的，同时每个输出还有一个偏置。

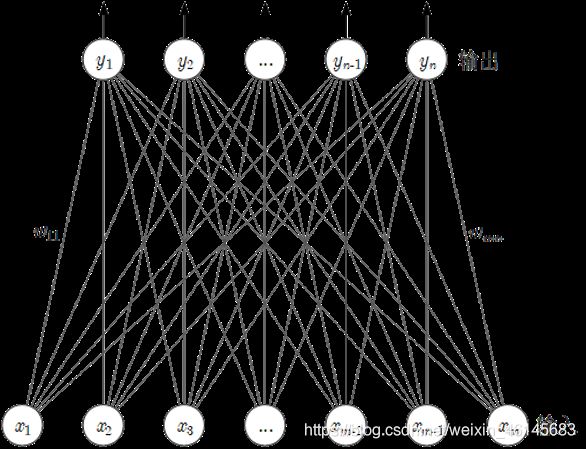
注意：全连接层的参数规模太大，远远超过共享的卷积层，因此通常采用的是全局卷积和1×1卷积形式来替代全连接层，其中全局卷积可以实现输入数据的展平，1×1卷积可以实现一维到一维的映射。
具有全连接层的卷积神经网络在某些场合中具备更好的鲁棒性和正确率。

1.6 目标函数

1.6.1 常用的损失函数

为了衡量学得的模型参数的好坏，可以用一个函数来度量模型预测值与真实值之间的差异，称之为损失函数（loss function）或者代价函数（cost function）。

交叉熵损失函数

目前最常用的分类任务损失函数是交叉熵（cross entropy）损失函数。交叉熵是信息论中的概念，主要用于度量两个概率分布之间的差异性。交叉熵损失函数又称为Softmax损失函数,表达式为：

其中，$m$为样本数,$N$是样本的类型数量，$x_i^j$为样本$S_i$对应的真实标签，$x_i^j$表示特征向量$x_i$的第$j$个分量(即公式内x_ij)。

均方误差损失函数（$L_2$损失函数）

反映的是样本真实值和模型预测值之差的平方的期望值，公式为：

平均绝对误差损失函数

主要用于回归任务，公式为：

1.6.2 正则化项

正则化是对学习算法的约束，目的是减少泛化误差（不是训练误差）。通常在神经网络模型中只对权值进行正则化约束。

$L_1$正则化

$L1$正则化是机器学习中一种常见的正则化方式，又被称作LASSO回归。假设待正则化的网络层模型参数为$w$，那么$L_1$正则化被定义为各参数绝对值之和，即公式为：
$\Omega (\theta )=||w|{|}_1=\left(\sum _i|w_i|\right)$
$L_1$正则化能够使得参数更加的稀疏。

$L_2$正则化

L2正则化又被称为岭回归（ridge regression）或Tikhonov正则，公式为：
$\Omega (\theta )=1/2||w|{|}_2^2=\left(1/2\sum _i{w}_i^2\right)$
通常称$L_2$正则化为权值衰减。

L1/L2混合正则化

中心损失正则化

1.7卷积神经网络的反向传播

1.7.1 全连接层的反向传播算法

多个全连接层相连可以看作是一个多层感知机，这里对符号约定如下：
①用 代表网络的第l层，$l=L$代表网络的最后一层；
②$W^l$、$b^l$分别表示第l层的权重矩阵与偏置向量；
③$\sigma (\cdot )$表示激活函数；
④ 表示第$l$层的输出向量，其中$u^l=W^l{y}^l/y+b^l$；
⑤$J$表示目标函数，其输出为标量。反向传播的目的就是要计算出J对于各层$W^l$、$b^l$的偏导数$\partial J/\partial W^l$和$\partial J/\partial b^l$ ，进而更新网络参数$W^l$、$b^l$，使得模型的预测值更加接近真实值。

1.7.2 池化层的反向传播算法

由于池化层并没有可学习的参数，因此不需要进行参数更新。池化层在反向传播过程中，只需要将下一层传递过来的梯度按照一定的规则传递给上一层。

最大池化的反向传播

平均池化的反向传播

1.7.3 卷积层的反向传播算法

卷积层可以看作是一种特殊的MLP神经网络，因此其反向传播过程与前面讨论的全连接层类似。

1.7.4 反向传播算法实例

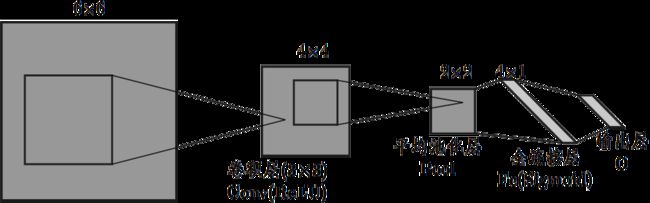
构建一个神经网络，包括一个卷积层$Conv$、一个平均池化层$Pool$、一个全连接层$Fc$和一个输出层$O$，输入为6×6像素的单通道，$Conv$层卷积核尺寸为3×3，步长为1，初始权值记为$Wconv$，偏置$b=1$，激活函数ReLU函数，Pool层池化核尺寸2×2，步长2，$Fc$层的输入为$Pool$层池化输出的展平，初始权值记为$W_f$,偏置$b_f=$ $[$ 1 1 ${]}^T$，激活函数为$Sigmoid$函数。网络输入数据记为$x$，真值为$Gt=$ $[$ 1 0 ${]}^T$，损失函数选择$MSE$损失函数。

1.8 典型的卷积神经网络结构

LeNet

AlexNet

VGGNet

GoogLeNet

ResNet

DenseNet

DenseNet的基本模块称为Dense Block，每个Dense Block都会接受前面所有Dense Block的特征图作为输入，以此缓解梯度消失的问题。连接到同一个Dense Block的多个输入采用的是维度层叠（Concat）的方式进行合并，而不是求和。

SPPNet

为了使网络能够接受不同尺寸的输入且保证性能不受影响，何恺明等人提出了空间金字塔池化（Spatial Pyramid Pooling, SPP），可以将任意输入转化为固定大小的输出，而不必关心输入图像的尺寸或比例。

SENet

提出了Squeeze-and-Excitation(SE)模块，SE模块首先对卷积运算得到的特征图进行挤压(squeeze)操作，得到通道级的全局特征，然后对全局特征进行扩张(excitation)操作，得到不同通道特征的权重，并以此为依据加权各通道特征图，获得最终的特征图。

MobileNet

MobileNet是Google提出的一种轻量化卷积神经网络，目的是希望为计算能力受限的移动和嵌入式设备如手机等提供一种高效的、与传统网络性能接近的神经网络架构。

MobileNet v1

使用深度可分离卷积来构建轻量级深度神经网络。

MobileNet v2

主要特性是引入了残差模块。

MobileNet v3

采用了神经网络架构搜索（NAS）来确定网络结构。