线段树Segment Tree(python代码实现)
线段树
线段树是一种二叉树(平衡二叉树),也被归类为二叉搜索树(广义上)。它是一种用于对区间修改、维护和查询的工具,可以优化时间复杂度至log级别。
基本思想
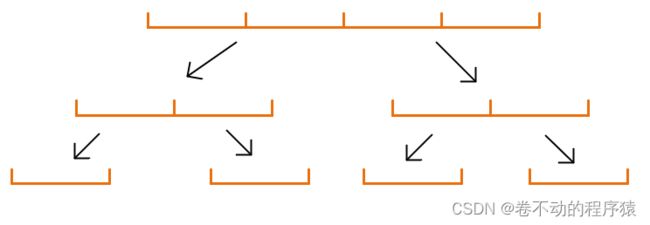
把一个大区间划分为两个小区间,然后把两个小区间分别划分为两个更小的区间,不断这样划分下去,直到区间内只有一个数据为止。 每个区间存放一个或者多个数据(比如:区间的和,区间的最大值,区间的最小值),以树的形式存放这些数据,则构成了一颗二叉树。 这种存放区间数据的二叉树就是线段树。
适合场景:
- 满足区间加法:区间的和,区间的差。
- 满足区间乘法:区间的乘积。
- 满足区间最值:区间最大值,区间最小值
不适合场景:
- 区间的众数
- 区间最长连续问题
- 最长不下降问题
线段树的维护:小区间的值更新大区间的值。
线段树主要分为三步:构建线段树,更新线段树(单点修改、区间修改),区间查询。
1、建树
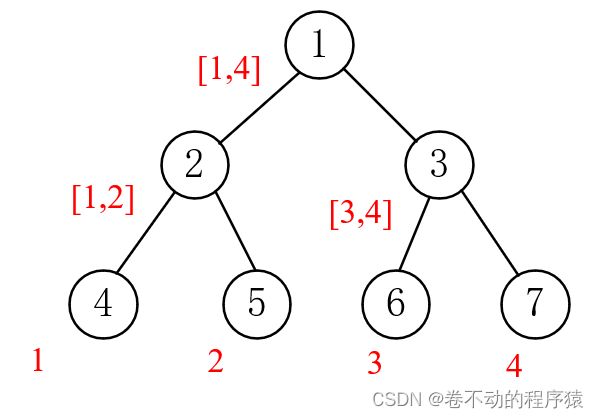
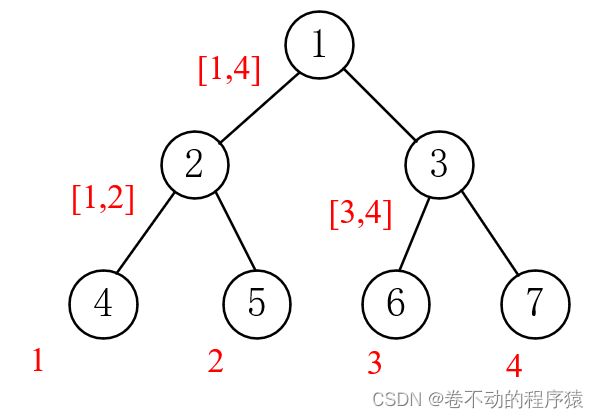
存储方式:堆
对于下标为i的结点,其左孩子的下标为2*i,右孩子的下标为2*i+1,父结点的下标为i//2(//表示整除)。
2、单点修改/区间修改
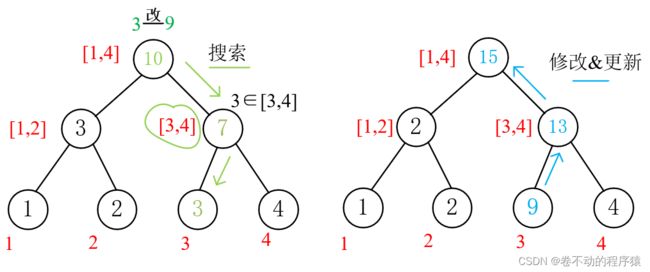
1)单点修改
·如果要查询的区间完全覆盖当前区间,就直接返回当前区间的值;
·如果查询区间和左孩子有交集,则搜索左孩子;
·如果查询区间和右孩子有交集,就搜索右孩子;
·最后合并处理两边查询的数据。
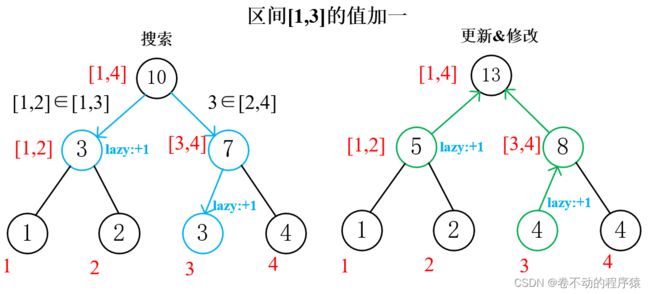
2)区间修改(需要使用lazy标记)
·如果要修改的区间完全覆盖当前区间,则直接更新这个区间,打上lazy标记;
·如果没有完全覆盖,且当前区间有lazy标记,先下传lazy标记到子区间,再清除当前区间的lazy标记;
·如果修改区间和左孩子有交集,就搜索左孩子;
·如果修改区间和右孩子有交集,就搜索右孩子;
·最后将当前区间的值更新。
lazy标记:将此区间标记,表示这个区间的值已经更新,但是它的子区间却没有更新,更新的信息就是标记保存的值。
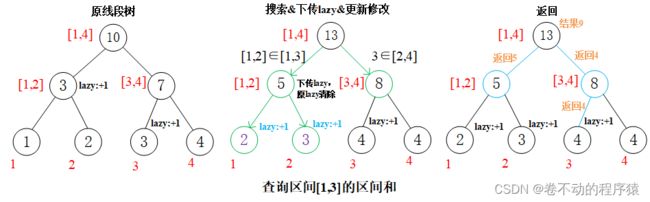
3、区间查询
·如果要查询的区间完全覆盖当前区间,就直接返回当前区间的值;
·如果没有被完全包含,则下传lazy标记;
·如果查询区间和左孩子有交集,搜索左孩子;
·如果查询区间和右孩子有交集,搜索右孩子;
·最后合并处理两边查询的数据。
python代码
# 构建树
def build_tree(arr, tree, node, start, end):
'''
:param arr: 数据列表(数组)
:param tree: 树结构(数组)
:param node: 结点
:param start: 数据数组的起始位置
:param end: 数据数组的结束位置
'''
#print(node, start, end)
# 递归出口(为叶子结点时,已经递归到最底部)
if start == end:
tree[node] = arr[start]
else:
mid = (start+end)//2 # 区间中间位置
l_node = 2*node+1 # 左孩子结点
r_node = 2*node+2 # 右孩子结点
build_tree(arr, tree, l_node, start, mid) # 递归计算左结点,(start, mid)左区间
build_tree(arr, tree, r_node, mid+1, end) # 递归计算右结点,(mid+1, end)右区间
tree[node] = tree[l_node] + tree[r_node] # 当前结点的值为左结点与右结点的和
# 更新树(单点修改)
def update_tree(arr, tree, node, start, end, index, value):
'''
:param index: 待更新的结点位置
:param value: 待更新的值
'''
# 递归出口
if start == end:
arr[index] = value
tree[node] = value
else:
mid = (start+end)//2 # 区间的中间位置(用来确定左右区间)
l_node = 2 * node + 1 # 左孩子结点
r_node = 2 * node + 2 # 右孩子结点
# 左区间
if (index >= start) and (index <= mid):
update_tree(arr, tree, l_node, start, mid, index, value)
# 右区间
else:
update_tree(arr, tree, r_node, mid+1, end, index, value)
# 更新结点的值
tree[node] = tree[l_node] + tree[r_node]
# 区间查询
def query_tree(arr, tree, node, start, end, L, R):
'''
:param L: 查询区间的起始位置
:param R: 查询区间的结束位置
:return: 返回查询区间内数值的和
'''
#print("start = {}".format(start))
#print("end = {}".format(end))
# 极端情况,不在区间范围之内
if R < start or L > end:
return 0
# 到达叶子结点(递归出口)
elif start == end:
return tree[node]
# 当整个右子树区间整个包含在查询区间内,直接返回当前结点的值(优化,防止做无用的查询操作)
elif L <= start and end <= R: # 剪枝
return tree[node]
else:
mid = (start+end)//2 # 区间的中间位置
l_node = 2 * node + 1 # 左孩子结点
r_node = 2 * node + 2 # 右孩子结点
# 左区间查询
sum_l = query_tree(arr, tree, l_node, start, mid, L, R)
# 右区间查询
sum_r = query_tree(arr, tree, r_node, mid+1, end, L, R)
return sum_l + sum_r # 返回区间结点的和
if __name__=="__main__":
print("--------构建---------------")
arr = [1, 3, 5, 7, 9, 11, 13, 17] # 数据
max_len = 100 # 设置线段树的大小
tree = [0] * max_len # 线段树
build_tree(arr, tree, 0, 0, len(arr)-1)
for i in range(15):
print("tree[{}] = {}".format(i, tree[i]))
print("--------更新---------------")
index = 5 # 位置
value = 1 # 更新值
update_tree(arr, tree, 0, 0, len(arr)-1, index, value)
for i in range(15):
print("tree[{}] = {}".format(i, tree[i]))
print("--------查询---------------")
L = 3
R = 6
res = query_tree(arr, tree, 0, 0, len(arr)-1, L, R)
print(res)