因果模型五：用因果的思想优化风控模型——因果正则化评分卡模型

我们调研因果模型的出发点在于要以一种新颖的因果视角去解决金融领域模型存在的问题，所以我们的落脚点也应该在如何应用因果的思想或方法，去提高评分卡模型的精度或者稳定度。这个领域的相关文献较少，我们以Causally Regularized Learning with Agnostic Data Selection Bias这篇文章为例，介绍一下该文提出的因果正则化评分卡是如何在因果思想和信贷评分卡应用之间真正架起一座桥梁，把因果推断融入逻辑回归的。

一、模型中的因果和相关

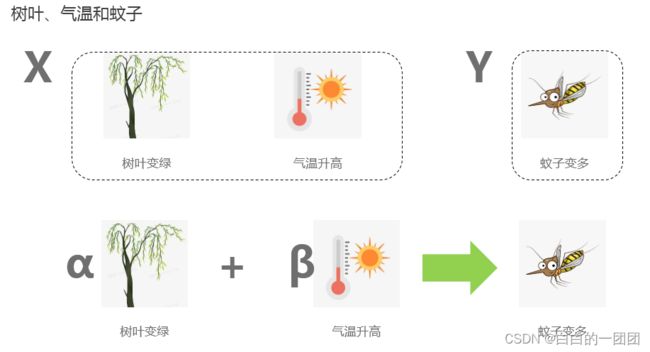
我们使用传统逻辑回归方法建立评分卡模型时，都不会去考虑变量与目标之间到底是因果关系，还是相关关系，只要变量有预测力，就能入模型。比如上图中，我们有两个变量：树叶是否变绿和气温是否上升，用来预测蚊子是否开始变多。如果不考虑去除变量相关性，我们建立的评分卡往往会将两个变量都融入进去，因为两个变量对蚊子是否变多都有很强的预测性。一旦我们观测到气温开始升高，河边柳树开始抽芽变绿，那不久蚊子就会变多，这种预测相当准确，虽然树叶变绿并不是导致蚊子变多的原因，但不影响我们做出准确预测。可以说，我们使用的传统评分卡都是这个情况。

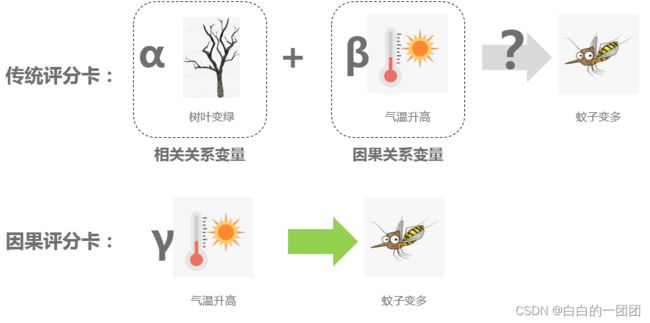
那这种情况有什么问题呢？我们看这样一个例子，假设现在我们应用评分卡的环境变了。这个环境里面，全是枯死的树，任你什么季节，它都不可能再有树叶变绿了。这个时候我们只观测到了气温升高，没有看到树叶变绿，用这样的评分卡预测蚊子是否变多变得不确定了，评分卡的效果大打折扣。这就不应该了，气温升高才是蚊子变多的根本原因，预测结果不应该受到树叶是否变绿的影响。
那有没有一种方法，能够让我们在建立评分卡的时候就排除掉那些只是相关，而非因果的变量，或者排除掉每个变量中相关的部分，只保留因果的部分呢？这样我们就能得到一个蚊子只和气温有关的因果评分卡。这样的评分卡效果就不会受环境变化的影响。

再来看文章中举的一个图像识别的例子。我们现在要建立一个识别图片中动物的模型，但在训练样本中，大多都是背景为草地的狗狗图片。如果使用传统的模型方法进行建模，那模型很容易会把绿草地当成一个重要的特征。如果我们用这样的模型去预测草地背景的狗狗图片时，那准确度还是相当高的。但问题出在需要预测的图片不都是草地背景，如果换成雪地中的狗狗图片，那传统模型的预测就失效了。所以我们需要一个真正能把握本质的因果模型，这样的模型能够提取出图片中最本质的特征（狗狗），而排除掉只有相关性的噪音特征（草地背景），才能保证模型在各种背景下都有效。

二、不可知样本选择偏差

我们例子中所列举的，训练时是春天会发芽的柳树，而预测时变成了全都枯死的树，或者一年四季树叶都绿的松树；或者图像识别中，训练时是绿草地上的狗狗，而预测时变成了雪地上或车里的狗狗，这种预测环境和训练环境不一样的现象，在学术上有个定义，叫做不可知样本选择偏差（agnostic selection bias），指的就是训练样本和测试样本分布不一致。当明确了这个定义，我们要解决的问题也就可以定义如下：
给定训练样本$D_{train}=(X_{train},Y_{train})$，其中$X_{train}$代表变量，$Y_{train}$代表标签。任务就是学习一个参数为$\theta$的分类器$f_{\theta }()$，去精准预测测试集数据$D_{test}=(X_{test},Y_{test})$的标签，其中测试集数据的分布和训练集不同${\Psi }_{train}\ne {\Psi }_{test}$。在不可知样本选择偏差的设定下，我们并不知道从训练集到测试集的数据分布是怎么转变的。

三、因果推断

问题已经定义清楚了，要解决这个问题，就需要引入一个因果模型的理论框架，这里选择的理论框架就是因果推断。

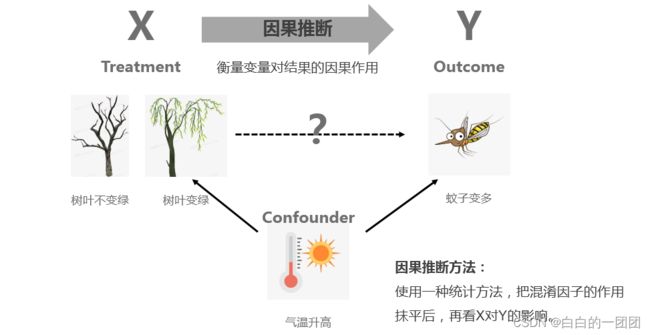
因果推断是干什么的呢？因果推断就是要通过一种统计方法，来衡量一个处理变量X（treatment）对输出变量Y（outcome）有多大的因果影响。就比如我们所举例的，树叶变绿会多大程度上导致蚊子变多。其实衡量一个因素对结果的影响，最直观有效的方法是AB测试，比如设置一个实验组，一个对照组，实验组中让树叶变绿，对照组中不让树叶发芽变绿，在同样的环境下，观测两组中蚊子变多的情况，如果有差异，则说明确实两者之间有因果关系。但问题是，不是所有场景都有条件给你做AB测试，比如放到风控领域，衡量一个人的品格和他是否逾期之间是否有因果关系，要怎么搞这样一个对照实验呢，就算能搞符合道德伦理吗？由此我们才不得不借助统计的方法，在观测数据上去尽可能地挖掘出变量与目标的因果关系，才有了因果推断这个领域的研究发展。
因果推断怎么实现用观测数据得到因果关系的呢，这要先介绍混淆因子（confounder），混淆因子可以理解为对照实验里的环境，就像例子中的气温升高。虽然我们能观测到树叶变绿和蚊子变多的强相关关系，但我们都知道这两者都是因为气温升高导致的，我们在研究树叶变绿和蚊子变多的关系时，这里气温升高就成了一个混淆因子。因果推断的基本思想就是通过一种统计手段，把实验组（treatment=1）和对照组（treatment=0）中所有的混淆因子都搞成0，或搞得尽量小，这种情况下再看处理变量和目标的相关关系，反映的就是因果关系了。

四、因果与评分卡的融合

了解了因果推断的思想后，接下来就要考虑怎么把因果推断融入到评分卡建模中。首先，因果推断中处理变量一般都只取值0和1，但建模变量不都是这样。这个问题容易解决，只需要对所有的建模变量都进行独热编码就可以了。其次，怎么定义哪些变量是处理变量，哪些是混淆因子呢，这个问题的处理方法是，把每一个变量当成处理变量来衡量对Y的因果作用时，就把其它所有变量都当成混淆因子。这看似简单粗暴，但在我们未知因果结构的时候是合理的操作（合理性可参考文章：Entropy balancing for causal effects: A multivariate
reweighting method to produce balanced samples in observational studies）。当解决了这两个问题后，我们要研究的问题可以进一步具体化如下：
给定训练数据集$D_{train}=(X_{train},Y_{train})$，其中X代表特征，Y代表标签，任务为如何联合地识别出所有变量对Y的因果贡献$\beta$，并基于$\beta$学习一个分类器$f_{\beta }()$。
那具体要通过什么样的统计方法来实现消除混淆因子的影响呢？这里使用的就是混淆平衡的方法。因为矩可以唯一确定一个分布，而混淆平衡方法通过调节样本权重W，来平衡掉混淆项的矩。具体公式如下，公式左边是处理变量为0时，样本混淆项的均值，公式右边这项代表处理变量为1时，样本混淆项的均值。我们要找的就是这样一个系数W，它能让处理变量为0和1时的混淆项的矩最小化。直观讲就是通过调节系数，来尽可能消除对照组和实验组的外部环境差异。

如果要把混淆平衡这个方法直接应用到评分卡建模中，也就是学习所有变量对目标的因果作用，就需要学习p x n个样本权重W，参数过多，不太可行。所以文中提出了一个包含所有变量的全局因果项：

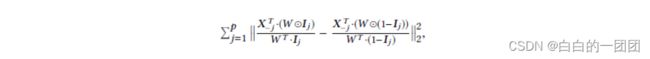
有了这样一个全局因果正则项后，也就有了把因果思想融入逻辑回归评分卡的抓手，评分卡的优化目标函数就可以写作：

直观的理解就是在混淆因子尽可能小的情况下，去寻找全局最优解。
进一步我们可以将目标函数写成如下形式。由于目标函数中有两个需要优化的参数，可以使用固定其中一个，优化另一个的思想去迭代优化。

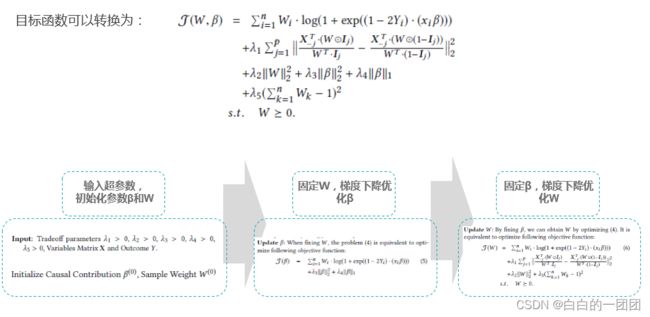
到此，整个因果正则化评分卡的训练过程可总结如下：
输入：正的权衡系数${\lambda }_i>0(i=1,2,3,4,5)$，全部0-1值编码后的变量矩阵X，指示编码自同一原始变量的index集合Sj，目标值Y。
输出：因果系数$\beta$和样本权重W
过程：

1. 初始化$\beta$和W
2. 计算当前的目标函数值$J(W,\beta )$
3. 按照上述固定一个，优化另一个的方法优化$\beta$和W，优化完后计算$J(W,\beta )$
4. 不断迭代优化，直至$J(W,\beta )$收敛或达到最大迭代次数
5. 返回系数$\beta$和W

五、模型效果评估

5.1 人工合成数据效果测试

合成初始变量X = {C, V}，其中C和V分别代表因果变量和噪音变量。C和V都从一个N(0,1)的正态分布中随机选取，取值上面进行二元化处理：大于0则取为1，否则取为0。同时，目标值Y由这样一个函数计算出来：$Y=f(C)+N(0,1)$，同样的方法将Y进行二元化。为了测试模型在有偏差样本上的的稳定性，需要随机塑造了一系列随环境变化的分布函数$P(Y|V)$，具体就是通过设置一个偏差系数$\gamma \in (0,1)$来控制$P(Y|V)$的变化，对每一个样本，如果V=Y，则该样本被选择的概率为$\gamma$，否则相应的概率则为$1-\gamma$，也就是$V=\gamma \ast Y+(1-\gamma )\ast (1-Y)$，这样，当$\gamma$大于0.5的时候意味着Y和V正相关，等于0.5的时候相互独立，小于0.5则代表负相关。如此，通过变化$\gamma$，一个未知的样本偏差就构造出来了。

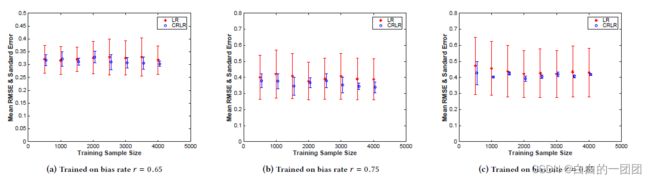
文中对比了$\gamma$在0.65、0.75和0.85三个取值下（左、中、右三张图），不同样本量情况下（横坐标），因果正则项评分卡（图中蓝色bar）和传统评分卡（红色bar）的RMSE。可以看到因果正则评分卡的拟合效果明显优于传统评分卡，而且$\gamma$越大，即未知样本选择偏差越大的情况下，因果评分卡的优势越明显。

5.2 YFCC100M图像数据测试

YFCC100M包含了海量的图片数据，这里选取了其中的10个类别（比如识别小鸟、汽车、猫、狗等）来测试不同模型对图像中动物识别的准确性，每个类别里面挑5个场景（比如识别狗的类别中有草地、雪地、沙滩、车里、大海五个场景）。为了突出不可知样本选择偏差，选择其中三个场景为训练集，另外两个场景分别为测试集和验证集。文中将因果正则化评分卡和另外五种模型或方法进行了效果对比，结果如图：

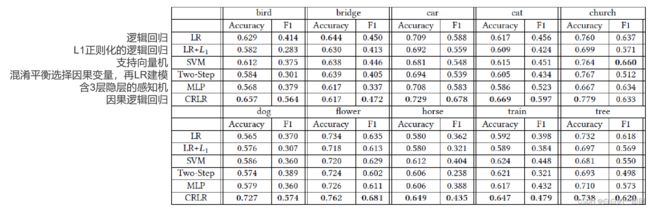
这里分别对比了传统逻辑回归、带L1正则化的逻辑回归、支持向量机、含3层隐层的感知机、以及两步法建模的效果。图中用准确率和F1 score来评判各个方法的效果，发现因果正则化评分卡确实在绝大部分情况下都明显优于其它方法。这里重点说一下两步法建模，两步法建模方法具体来说就是先用混淆平衡的方法在所有建模变量中选择和目标有因果关系的变量，然后只用这些因果变量建立逻辑回归模型。这个方法也是为了解答一个常识性问题，即如果我只把因果性的变量挑出来建模，是不是也能达到同样的效果，其实也就没必要这么麻烦搞一个因果正则化的评分卡方法呢？从实验结果来看，答案是不行。要想兼顾效果与稳定性，还必须得把因果思想和全局最优拟合两者结合起来，让因果和效果达到一种博弈平衡，才是我们想要的最优解。这就像信贷业务中，风控部门负责控风险，业务部门负责做大量，一个在给业务踩刹车，另一个给业务踩油门。我们不能一味只追求把风险降到最低，这样就没量了，也不能一味只图扩大客户量，这样风险就兜不住了。只有在两者相互制衡，博弈平衡下，才能保证业务长久、稳定、良性地发展。
那到底这个因果正则化模型是怎么做到比其它模型效果更优的呢？文中以几个图片为例，对比了因果模型和传统逻辑回归的的几个主要特征，如下图所示：

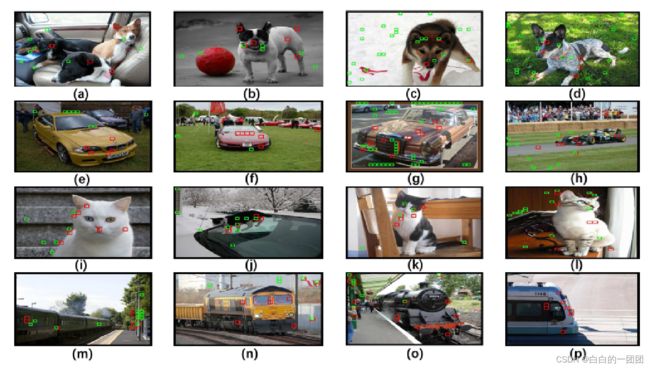
图中红色小方块标注的就是因果正则化评分卡的几个主要特征的落点，而绿色小方块标注的是传统评分卡的主要特征落点。可以看到因果正则化评分卡确实做到了抛开现象看本质，比较准确地定位到了反映本质的动物或者车辆的轮廓与特征，而传统评分卡总是将环境中的一些噪音信号当成主要特征。这也是为什么因果评分卡效果更优的原因。

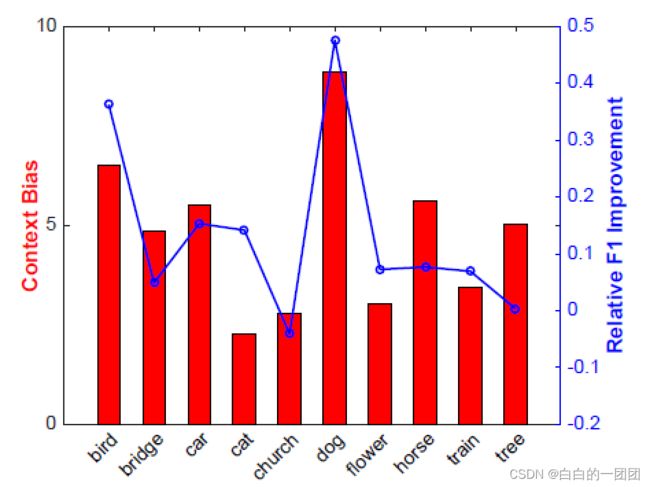
进一步，文中对比了十个场景中不可知选择偏差（红色柱状图）和因果评分卡相对传统评分卡的效果提升（蓝色线装图）的关系，可以看到，结论和人工合成数据的结论是一致的，即偏差越大，因果评分卡的效果提升就越明显。

5.3 office_caltech图像数据测试

office_caltech数据集包含四个不同的域，分别是amazon，caltech，dslr，webcam；每个域包含10类图像。同样，文中用上述6种方法，对四个域中的数据进行交叉跨域训练测试，比如用amazon的数据训练模型，用dslr数据测试模型效果。实验结果如下：

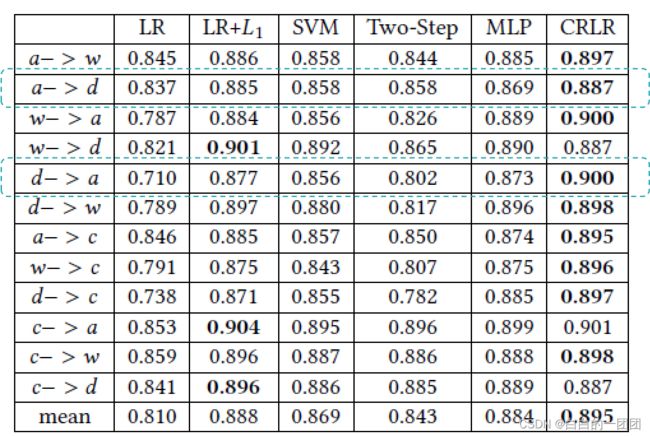
不出意外地，因果正则化评分卡（CRLR）的效果在大部分情况下都是最优的。这里要重点说明的就是amazon的数据量远大于dslr，用dslr数据训练模型，预测amazon数据带来的效果提升，远大于用amazon训练模型，预测dslr数据带来的提升。这样一个实验结果也暗示出，因果评分卡在没有充足训练数据时效果提升是更明显的。

5.4 微信广告数据效果测试

这里用微信广告数据，是要建立一个二分类模型，即预测客户最终选择了喜欢还是不喜欢，数据中有56个特征，类似性别、年龄、朋友数、设备等等。

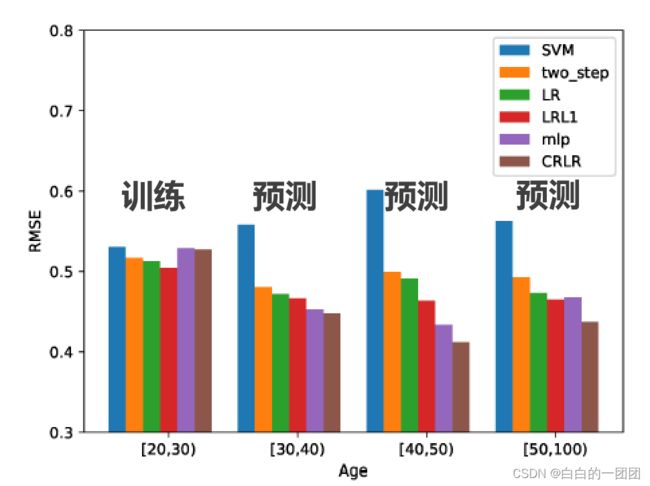
这里选择的测试方法是先把微信客户用年龄进行分层，然后用20-30岁的客户进行模型训练，再用其它3个年龄段的客户数据来测试模型效果。毫无意外，因果正则化评分卡的RMSE在6个模型中是最低的，效果最好。但值得注意的是，在训练集（20-30年龄段）本身上面，因果正则化评分卡的效果其实还是比较差的。这也是可以理解的，因为毕竟因果正则化评分卡的目标函数要兼顾着因果关系的发现，在没有样本选择偏差的情况下，当然比简单粗暴拟合全局最优的效果差一些。

5.5 真实金融风控数据效果测试

在真实的零售信用场景中，积累足够的数据需要很长的时间，用来建模的样本往往是几个月前或者一两年前的数据，这自然避免不了跨样本集上未知样本选择偏差的问题。而这些数据刚好可以验证因果正则化评分卡的效果。
值得一提，这里的测试结果来着另一篇文献：Causal regularization for Stable Scoring Card Model。这里基本照搬了因果正则化评分卡方法，进行了小小的改动（原文中方法：a、b、c三个变量，独热编码后变成a1、a2、a3、b1、b2、b3、c1、c2、c3九个变量，考察a1的因果关系时，就把其它所有变量当做混淆因子；改动后的方法：考察a1的因果关系时，只把b、c衍生出的变量当做混淆因子），并在金融零售风控数据上测试了效果。文中用来测试的数据选自一个全国金控集团的一条新的信贷业务线，三个月的数据中，前一个月用来做训练集，后两个月做测试集。训练集有3361个好样本和33个逾期样本，测试集有4965个好样本和49个坏样本。这里选入模型的变量有二十个，包括消费等级、净资产、贷款额度、水电气缴费情况，通讯费用等等。

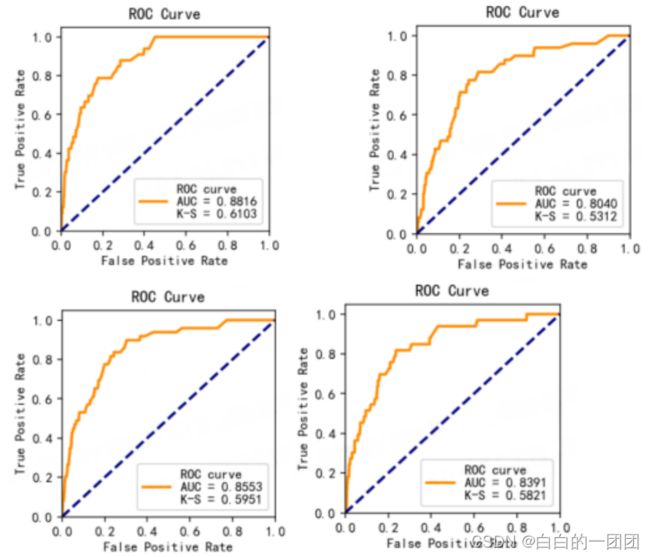
模型效果如上图所示，上面两幅分别代表传统评分卡模型在训练和测试集上的效果；下面两幅代表因果评分卡在训练和测试集的效果。可以看到因果评分卡的稳定性和传统评分卡相比显著提升，传统评分卡在测试集上的KS值相较于训练集下降了8个点（61 vs 53）；而因果评分卡的KS值在训练和测试集上几乎保持一致（0.59和0.58）。

六、因果正则化评分卡的应用场景探讨

当我们了解了因果正则化评分卡的原理和实验结果后，就能比较清楚地知道它适合于应用在什么场景下。大概可以总结为以下三点：

• 1、训练样本和测试样本之间有着明显的不可知样本选择偏差。这是因果正则化评分卡这个方法被提出来的基本前提，要解决的就是这个问题。从微信广告数据中也可以明显看到，存在明显的样本选择偏差才能体现出因果评分卡的优势，如果没有这种偏差，因果评分卡的效果还不如其它模型算法。
• 2、训练样本要涵盖跨域特征。就比如本文中训练识别狗狗的模型，把三个场景下的狗狗图片作为了训练数据，就能够让模型通过对比充分捕捉到反映的本质的狗狗特征。如果只用一种场景下的狗狗图片做训练样本，模型效果应该会大打折扣。
• 3、在没有充足训练样本的情况下，因果评分卡效果优势更显著。Office_caltech数据集的测试结果能充分说明这一点，样本量越充足，因果评分卡的优势越弱。

由此来看，如果我们的业务中面临的情况是：市场环境变化较快、或者需要用业务A的数据训练模型，去冷启动全新业务线B，而且训练样本不太充沛，并且训练样本中客群丰富，能够涵盖跨域特征。这种情况下，可以尝试一下因果评分卡建模，预期效果和稳定性有可能好于传统模型。

参考文献：
Causally Regularized Learning with Agnostic Data Selection Bias
Causal regularization for Stable Scoring Card Model

---

最后，欢迎参看其它因果模型相关的探索：
因果模型一：因果模型入门综述
因果模型二：线性非高斯无环模型
因果模型三：因果模型在解决哪些实际问题
因果模型四：实现因果模型的python工具——pycasual