MR-GMMapping:基于高斯混合模型的通信高效多机器人映射系统

论文

III. 通过高斯混合模型建图（MAPPING VIA GAUSSIAN MIXTURE MODELS）

  GMM是一种使用不同加权高斯分布来表示某些概率分布的概率模型。GMM的概率密度函数定义为

$$p(x)=\sum _{k=1}^N{\pi }_k\mathcal{N}\left(x\mid {\mu }_k,{\Sigma }_k\right)(1)$$
其中每个分量都是高斯分布$\mathcal{N}(x|{\mu }_k{\sum }_k)$，均值为${\mu }_k$、协方差矩阵为${\sum }_k$。${\pi }_k$是每个高斯分布的权重，且满足${\sum }_{k=1}^N{\pi }_k=1$。通过EM算法[25]可以优化得到唯一的GMM参数集合$\Theta ={\left\{{\pi }_k,{\mu }_k,{\Sigma }_k\right\}}_{k=1}^N$。

  假设机器人在感知环境时，总共获得$M$帧点云。设$V=\{V_j{\}}_{j=1}^M$为所有点云，$V_j$为第j帧的数据。考虑映射坐标变换，我们将参数集扩展为
$$\Theta =\left\{{\left\{{\pi }_k,{\mu }_k,{\Sigma }_k\right\}}_{k=1}^N,{\left\{R_j,t_j\right\}}_{j=1}^M\right\}(2)$$
其中$R_j\in {\mathbb{R}}^{3\times 3}$是旋转矩阵，$t_j\in {\mathbb{R}}^3$是平移向量。

  在多机器人建图系统中，$V$通过在集合中加入新的点云$V_j$进行扩展，$\Theta$通过集成新的GMM子映射进行更新。机器人进行权值归一化，满足${\sum }_{k=1}^N{\pi }_k=1$。

IV. 多机器人GMM建图（MULTI-ROBOT GMM MAPPING）

A. GMM子地图建立（GMM Submap Construction）

  GMM地图的构造直接影响其在机器人应用中的性能。submap-based框架，例如SMMR-Explore[7]适合于多机器人系统，因为在通信密集（communication-intensive）的场景下，机器人只转移协作探索的子地图。然而，在多机器人系统中，机器人使用GMM子地图进行相对定位，直接合并GMM帧来构建子地图可能会导致地图构建失败。

  如图2(a)所示，两个机器人沿着各自的轨迹运动并感知同一场景。子图提取策略[22]根据每个传感器输入生成对应的GMM帧，然后将这些GMM帧根据权值（归一化后的权值）归进行整合[如图2(b)]。虽然通过上述方法构建的GMM子地图能够正确描述场景的占用状态，但是不同的观测路径导致高斯分量的分布和权重不一致。子地图中高斯分量权重的不同可能导致基于GMM的PR（place recognition）失败，子地图中高斯分量分布的不同可能导致基于GMM的地图匹配失败[如图2©和(d)上半部分所示]。综上所述，GMM子地图面临两个挑战:1)不同的GMM分量权重可能导致GMM子地图的PR描述符无法匹配;2) GMM分量分布的不同可能使两个GMM子地图中所有高斯分量的L2范数平方和难以收敛。为了解决这个问题，我们将相邻的点云集成在一起，而不是一帧一帧地构建GMM地图。在确定一个子图后，我们对整个点云进行体素过滤，去除重复信息，然后使用EM算法生成一次GMM子图[如图2©和(d)的下半部分]。这样，GMM子图中高斯分量的权重可以正确反映真实环境中点云的分布，提高了场景匹配和地图配准的精度(实验结果见第VI-B节)。

  在实现方面，我们的GMM子图构建包括三个步骤:子图构建、子图传输和基于子图的轨迹优化。每个GMM子图都按顺序执行这些步骤，而这些步骤运行在三个独立的线程中。

  子图构建（Submap Consturction）：每个机器人有一个PointBuffer (PtBuffer)，用来临时存储每个子图的点云。当接收到新的点云帧时，机器人在PtBuffer中进行体素过滤，去除重复点。每个GMM子图由40帧点云生成，这保证了每个GMM子图中足够的环境特征用于PR，同时也保证了用于地图匹配时描述同一场景的GMM子图的相似性。机器人从缓冲点生成GMM子映射(在第IV-B节中介绍)，然后为每个GMM子图提取场景描述符，为后续的PR步骤做准备。

  子地图传输（Submap Transmission）：当机器人收到其他机器人发布的GMM子地图后，依次进行PR和地图注册步骤(详见第五节)。

  基于子地图的轨迹优化（Submap-based Trajectory Optimization）：机器人使用子图传输的RelPose的结果执行后端优化。优化变换(TF)在TFGraph中更新，TFGraph是我们提出的用于维护多个机器人TF树的数据结构。当机器人操作系统(ROS)查找两个机器人之间的相对位姿时，TFGraph可以防止不同机器人的TF树形成循环。

B. 自适应模型选择（Adaptive Model Selection）

  组成GMM的高斯分量的数量直接影响到机器人之间的数据传输。由于现实世界中的点云分布不均匀，直接通过EM算法生成GMM图可能会浪费其表示能力。例如，即使是向下采样，对地板采样后得到的点数量也远远高于对墙壁采样得到的点数量。因此，在没有GMM模型选择的情况下，会出现重叠的高斯分量[图3(a)]。这导致了多机器人系统传输时存在过多的冗余信息。在MR-GMMapping中，机器人在子图构建（submap Construction）线程中确定一个submap后进行Adaptive Model Selection（自适应模型选择），以解决该问题。

  如果预先给出高斯分量的个数，小区域的子图可能在形状和位置上有相似的分量。从室内场景下高分辨率RGBD相机获得的点云中，我们观察到点云来自障碍物表面，因此大部分高斯分量是平坦的。我们将特征值的方向定义为每个高斯分量的主方向。机器人首先根据其主方向对代表不同方向平面的高斯分量进行分类。然后，机器人将均值向量作为高斯分量的物理位置，将每个类别划分为更多的子集。最后，机器人使用Kullback-Leibler (KL)发散度[26]来合并每个子集中相似性较高的分量。由于环境特征的剧烈变化，机器人可能会出现一些不可避免的失配。因此，我们的GMM模型选择策略是在数据传输和映射精度之间进行权衡，但仍然可以提高GMM参数的利用效率。

  设$N$个重叠高斯分量$\theta$在相似的物理位置(用${\mu }_n$表示)和形状(用${\sum }_n$表示)上相似。$n_k$是由第$k$个高斯分量表示的点数。我们认为每个高斯分量可以代表大量的点，所以每个分量代表的点的数量$n_k\to \infty$。公式(3)表示$x_i^k$为第$k$个高斯分量中的第$i$个点的点集。
$${\left\{x_i^k\right\}}_{i=1}^{n_k\to \infty }\sim \mathcal{N}\left({\mu }_k,{\Sigma }_k\right)(3)$$

  我们采用对角矩阵${\sum }_k$来减少生成GMM地图的延迟[27]、[28]，而${\sum }_k$在转换为其他机器人坐标后可能变为非对角。

  我们设合并后的高斯分量为$\{\pi ,\mu ,\sum \}$，参数可由(4)-(6)计算，其中$x_i^k\in {\mathbb{R}}^3$，${\mu }_k\in \mathbb{R}3$， ${\sum }_k=diag\{{\sigma }_1，{\sigma }_2，{\sigma }_3\}$，向量的平方由外积定义。

$$\begin{array}{rl}& \pi =\sum _{k=1}^N{\pi }_k\\ & \mu =\underset{\begin{array}{c}{n}_k\to \infty \\ k=1\dots N\end{array}}{\lim }\frac{{\sum }_{k=1}^N{n}_k{\mu }_k}{{\sum }_{k=1}^N{n}_k}=\frac{{\sum }_{k=1}^N{\pi }_k{\mu }_k}{{\sum }_{k=1}^N{\pi }_k}\\ & \begin{array}{rl}\Sigma =& \underset{\begin{array}{c}{n}_k\to \infty \\ k=1\dots N\end{array}}{\lim }\frac{{\sum }_{k=1}^N{\sum }_{i=1}^{n_k}{\Vert x_i^k-\mu \Vert }^2}{{\sum }_{k=1}^N{n}_k-2}=\underset{\begin{array}{c}{n}_k\to \infty \\ k=1\dots N\end{array}}{\lim }\frac{1}{{\sum }_{k=1}^N{n}_k-2}\cdot \\ & (\sum _{k=1}^N(\sum _{i=1}^{n_k}{\Vert x_i^k-{\mu }_k\Vert }^2+n_k{\Vert {\mu }_k-\mu \Vert }^2\\ & +2\sum _{i=1}^{n_k}\left(x_i^k-{\mu }_k\right)\left({\mu }_k-\mu \right)))\\ =& \underset{\begin{array}{c}{n}_k\to \infty \\ k=1\dots N\end{array}}{\lim }\sum _{k=1}^N\frac{\left(n_k-1\right){\Sigma }_k+n_k{\Vert {\mu }_k-\mu \Vert }^2}{{\sum }_{k=1}^N{n}_k-2}\\ =& \sum _{k=1}^N\frac{{\pi }_k\left({\sum }_k+{\Vert {\mu }_k-\mu \Vert }^2\right)}{{\sum }_{k=1}^N{\pi }_k}\end{array}\end{array}$$
  由于高斯分量的权重可以表达不同GMM映射所描述的点个数之间的关系，(5)和(6)可以简化为只包含GMM参数而不包含点云信息的表达式。

V. GMM地图的应用（APPLICATIONS WITH GMM MAP）

A. GMM位置识别（GMM Place Recognition）

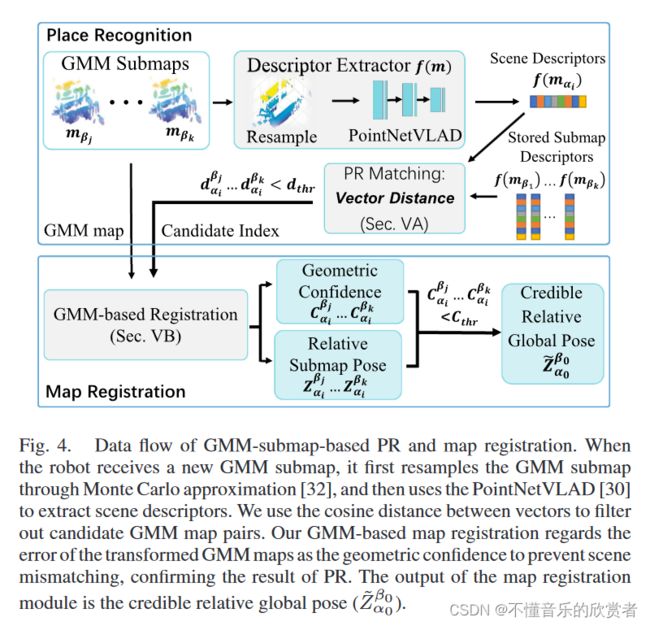
  PR是机器人用来判断它们是否到达（观察）到同一个场景的过程。以前的多机器人PR工作使用基于视觉的方法来提取场景描述符，如BoW[29]和NetVlad[13]。其他基于子地图的PR方法利用来自不同机器人[7]的占用栅格地图。然而，在通信受限的环境中，在机器人之间传输传感器数据或栅格地图是不太现实的。为了使基于GMM的PR成为可能，我们设计了一个基于GMM的描述符提取器$f(\cdot )$用来从GMM子图列表$m_{{\alpha }_i}$中计算子图的描述符$f(m_{{\alpha }_i})$。

  如图4所示，我们的$f(\cdot )$由两个部分组成:1)从$m_{{\alpha }_i}$中重新采样3D点云，2)PointNetVLAD[30]，它将3D点云编码为一个描述向量。我们定义$d_{{\alpha }_i}^{\beta j}$为向量$f(m_{{\alpha }_i})$和$f(m_{{\beta }_j})$之间的余弦距离[31]。PointNetVLAD在相同场景$m_{{\alpha }_i}$和$m_{{\beta }_j}$下降低$d_{{\alpha }_i}^{{\beta }_j}$，而在不同场景$m_{{\alpha }_i}$和$m_{{\beta }_j}$下相对提高$d_{{\alpha }_i}^{{\beta }_j}$。在我们的MRGMMapping中，每个机器人在本地计算场景描述符，而不是频繁地在机器人之间共享描述符。一旦机器人接收到一个新的子地图，它选择距离低于给定阈值$d_{thr}$的GMM子地图用于后续的RelPose;其他的都被过滤掉了。

B. GMM地图注册（GMM Map Registration）

  地图注册模块对由PR模块提供的候选子图对（the candidate submap pairs）的相对变换进行估计;它会过滤掉误差大的结果。先前的工作提出了GMMreg[33]，一种健壮的分布式对分布式（distribution-to-distribution）配准方法，可在地下环境中实现GMM建图和导航。在GMMreg中，训练优化器来降低两个映射的高斯分量之间的误差。为了扩展GMMreg的思想，我们做了两个改进，使其更适合于多机器人系统。首先，我们使用地图注册作为防止PR错配的手段，因为配准结果容易受到错误的位置关联的影响。我们把GMMreg优化器的最终损失看作相对位姿$z_{{\alpha }_i}^{{\beta }_j}$的几何置信度$C_{{\alpha }_i}^{{\beta }_j}$。然后，过滤出几何置信度大于阈值$C_{thr}$的候选对。第二，在多机器人系统中，来自不同机器人的GMM子图可能具有不同数量的高斯分量。因此，我们调整了具有不同分量数量的GMM子图的损失函数。

C. 基于GMM的局部规划器（GMM-Based Local Planner）

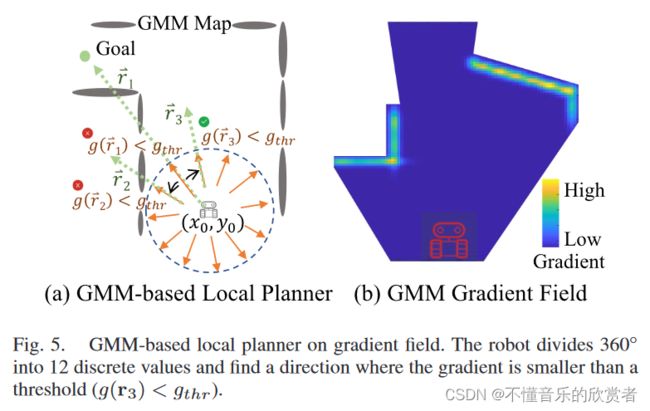
  局部规划器基于GMM地图的梯度场。如公式(1)所示，$p(x_0,y_0)$为某一位置$(x_0,y_0)$的占用概率，其中梯度向量为$g(x_0,y_0)=\nabla p{|}_{x=x_0,y=y_0}$。梯度向量$g$在$r$方向上的分量记为$g(r)$。在实现中，我们选择$r$方向上的两个相邻点来计算梯度$g(r)=li{m}_{ϵ\to 0}=\frac{f\left[(x_0,y_0)+ϵ\times \mathbf{r}-f(x_0,y_0)\right]}{ϵ}$。图5(b)为g的梯度场。

  图5(a)展示了基于GMM的局部规划器。我们将机器人周围360◦划分为12个离散的方向，并设置方向(${\mathbf{r}}_1$)直接连接机器人的位置和目标作为候选移动方向。如果沿着${\mathbf{r}}_1$的梯度(记为$g({\mathbf{r}}_1)$)小于阈值$g_{thr}$，机器人将向${\mathbf{r}}_1$方向移动。但是，如果$g({\mathbf{r}}_1)>g_{thr}$，则表示在这个方向上会遇到障碍。然后选择周边方向作为候选方向[图5(a)中的${\mathbf{r}}_2$和${\mathbf{r}}_3$]，如果$g({\mathbf{r}}_2)<g_{thr}$或$g({\mathbf{r}}_3)<g_{thr}$，机器人将向r2或r3方向移动。如果仍然不满足，我们将选择更外围的方向作为候选方向，直到一个方向的梯度小于$g_{thr}$。在这种方法中，我们使用GMM地图来实现局部规划，而不是将它们转换为栅格地图。这验证了GMM直接用于本地导航的潜力、并说明GMM地图应用场景的可扩展性。

VI. 实验（EXPERIMENTS）

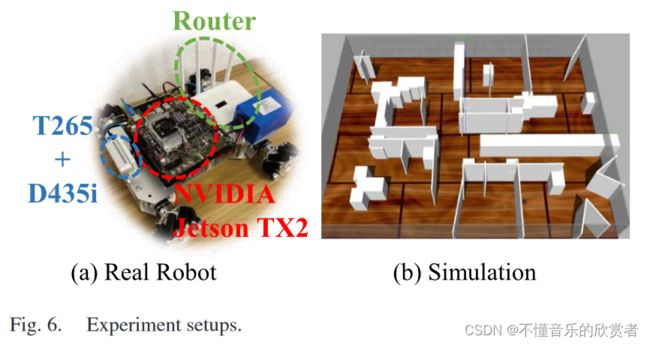
  先前关于GMM映射的工作已经报道了大量关于表示能力[19]的实验结果。我们在不同尺度的Gazebo模拟器[7]和真实机器人(如图6所示)中实现了我们的系统。我们的机器人配备了Intel RealSense T265[34]，它使用视觉SLAM技术实现了机器人姿态的实时采集，深度相机D435i[35]从环境中获取点云。在计算方面，我们使用了NVIDIA Jetson TX2，它具有4核ARM CPU和嵌入式GPU。为了保证在低通信带宽下数据传输的稳定和实时，我们设计了一个独立的路由器，而不是使用TX2网口。我们的机器人使用局域网来共享GMM子图。实验结果证明，我们提出的GMM子图这种方法能够执行PR(节VI-A)、地图注册(节VIB)和本地路径规划(节VI-C)。在系统级别上，MR-GMMapping的数据传输要小得多(第VI-D节)。

A. 地点识别（Place Recognition）

  我们将基于GMM的PR与Oxford RobotCar数据集[36]上的PointNetVLAD[30]进行比较。Oxford RobotCar采集的点云数量固定，坐标均值为零。对于基于GMM的PR和基于点云的PR，我们使用从PointNetVLAD训练的相同模型。图7显示了数据集中每个数据库对的前25个匹配的每个模型的召回曲线。我们的方法与PointNetVLAD具有类似的性能。对于Top 1%的召回，基于GMM的PR可以达到87.4%，而基于点云的PR可以达到88.3%。在实际应用中，这一微小的差异并不会影响PR在真实机器人上的性能。

  我们还测试了当机器人利用地图注册的置信度进一步确认PR结果时，精度-召回（precision-recall）曲线的改善情况(如图8所示)。然而，多机器人SLAM系统容易出现PR错配，需要消耗额外的计算量和通信资源来处理PR错配[5]。因此，我们更关注的是的低赔率时的高召回率(召回率在精度-召回率曲线的高精度范围内)。我们将PR与地图配准相结合，并选择基线作为基于点云的PointNetVLAD与ICP。我们选取70%场景识别准确率对应的基线，比较基于GMM的PR与基于GMMreg的PR与基于ICP的点云PR的结果。采用两种ICP方法进行点云配准:原始ICP和GICP[37]，两者的配准结果相差不大。我们使用点云库(PCL)[38] 1.8版本来计算ICP和GICP。之后,我们使用GMMreg作为注册步骤GMM-based公关,和ICP point-cloud-based公关后注册步骤。配准步骤可以提高基于GMM和基于点云的PR的召回精度(见图8中上面的矩形框)。在PR的整体改进方面，我们基于GMM的方法比基于点云的方法在同样高精度的情况下获得了更高的召回率(如图8下面矩形框所示)。

B. 地图注册（Map Registration）

  我们采用了两种不同的子图提取策略，并在TUM数据集[39]上对freiburg3长办公室户RGBD序列进行了实验。构建子图的方法有两种:

• A.拼接相邻的GMM地图帧(GMM+GMM子图);
• B.存储点云并一次性生成GMM子图(本文方法中为点到GMM子图)。

我们对这两种类型的子图使用GMMreg[33]，对基于点云的基线使用GICP来执行地图注册。我们通过集成5帧序列对点云进行预处理，因此序列的全部2509帧被分为大约500个GMM子图。5帧作为一个子图是可行的，因为它使子图能够描述相同的场景，同时具有一定的重叠程度便于用于地图配准评估。此外，我们的实验表明，多帧或少帧的子地图并不能提供更高的配准精度。

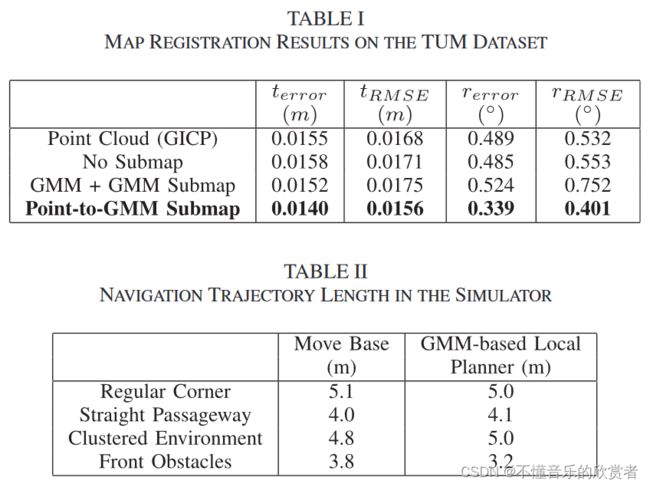  表一给出了轨迹位姿的平均误差和均方根误差(RMSE)的结果。我们使用TUM数据集[39]提供的评估工具包来计算这些结果。结果表明，点到GMM子映射的配准效果优于GMM+GMM子地图。我们认为这是因为在GMM帧积分和权值归一化之后，环境的总体概率描述被破坏了。这影响了精度，特别是那些旋转角度大的子地图。虽然逐帧地图配准(无子地图)的精度与点云到GMM子地图配准相比仅略有下降，但这使得多机器人系统之间大量的数据传输是不可行的。

C. 基于GMM的局部规划（GMM-Based Local Planner）

  我们比较了基于GMM的局部规划器和ROS Move Base40在四个不同模拟场景中的轨迹长度：规则角落(场景1)、直线通道(场景2)、集群环境(场景3)和前方障碍(场景4)。我们基于GMM的局部规划器和Move Base规划长度相似的路径。在机器人需要大角度转弯的场景中，如场景1和场景4，我们的方法的轨迹长度小于Move Base的。我们相信这是因为我们基于GMM的本地规划更倾向于走最短的路径，而Move Base使用Costmaps保证机器人的安全。基于GMM的本地规划器对移动方向上的障碍非常敏感。通过实时路径重新规划，使机器人远离障碍物。而当机器人在移动的方向上没有发现障碍物时，它不考虑障碍物的距离，直接沿着最短路径向局部目标移动。

  在这项工作中，我们使用GMM地图来实现局部规划，而不是将它们转换为栅格地图，并在一些简单的场景中进行验证。实验显示了GMM直接用于局部导航的潜力，扩展了GMM地图的应用场景。

D. 多机器人系统中的数据传输（Data Transmission in Multi-Robot System）

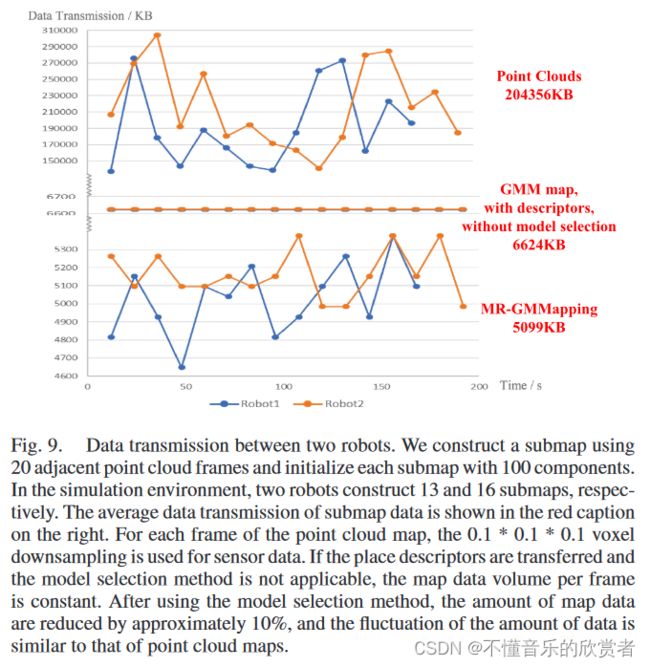  图9显示了在我们的仿真环境中两个机器人的子地图的数据传输。经过向下采样和新信息检查，在子图中添加新点云的速度约为每帧0.6秒。我们使用20帧点云确定GMM生成的子图，以确保每个子图包含足够的位置识别环境信息。在200秒的探索中，两个机器人分别构建了13帧和16帧的子地图。机器人传输点云时，平均子图数据量为204356 KB。如果机器人传输带有100个高斯分量和1024 KB场景描述符的GMM子地图用于位置识别，则平均子地图数据量为6624 KB。而在MR-GMMapping中，机器人在模型选择后不带描述符地传输GMM子映射，使平均数据传输减少到5099 KB。此外，我们可以看到MR-GMMapping中点云与GMM子图之间的数据量变化趋势是相似的，证明我们的模型选择方法可以根据环境的尺度有效地减少冗余信息。

  总之，与点云图相比，MR-GMMapping减少了约98%的数据传输。与带有描述符的GMM映射相比，MR-GMMapping减少了约23%的数据传输。一方面，我们消除了机器人之间的描述符传输，减少了15% (1024 KB)的数据传输。另一方面，我们的模型选择方法可以提高GMM元素的表达能力，减少约8%(约500 KB)的数据传输。我们通过合并冗余的组件来为环境选择最优的组件数量。这两种技术可用于不同环境下的多机器人GMM SLAM，减少数据传输。

VII. 结论与未来工作（CONCLUSION AND FUTURE WORK）

  这篇论文提出了一个通信高效的多机器人GMM地图系统，具有三个基于子地图的机器人应用：地点识别、地图注册和本地规划器。子图提取完成后，机器人可以完成以上三个应用。通过使用我们的组件级模型选择方法，机器人可以消除子图内部和子图之间的冗余高斯分量。MR-GMMapping中的机器人只传输GMM子图，这不仅使数据传输总量减少了98%，而且使RelPose的平均平移误差降低了11%，平均旋转误差降低了30%。

  由于协同探测是多机器人系统的基本任务，我们计划在未来提出新的多机器人探测方法，可以集成到GMMapping方法中。此外，我们还计划将MR-GMMapping扩展到利用3D地图的无人机(UAV)应用。

工程配置

  论文配套代码链接如下gmm_map_python。代码适配环境为Ubuntu 18.04（ROS melodic）、python2.7，但是在我自己配置的过程中，发现部分库不支持python2.x，配置起来比较麻烦，所以就直接基于Ubuntu 20.04（ROS noetic）、python3.x 进行配置，具体配置如下：

依赖

1. Pytorch for Place Recognition

   pip3 install torch torchvision
   

2. Python-PCL

   sudo apt-get install python3-pcl
   

3. GTSAM

   pip3 install gtsam
   

4. Other

   sudo apt install ros-noetic-tf2-ros
   sudo apt install ros-noetic-octomap-rviz-plugin
   sudo apt-get install ros-noetic-tf2-sensor-msgs
   pip3 install autolab_core
   pip3 install sklearn
   pip3 install future
   pip3 install transforms3d
   pip3 install pygraph
   

5. 修改pygraph：
   pygraph库只支持python2.x，不支持python3.x，因此需要修改pygraph库：

   gedit ~/.local/lib/python3.8/site-packages/pygraph/functions/planarity/kocay_algorithm.py
   

   将其中其中1061、1070行的except Exception, e:修改为except Exception as e:。

6. 修改.py文件权限

   cd src/gmm_map_python/gmm_map_python/script/
   chmod +x *.py
   

7. 修改.py文件适配python3.x
   github上代码是适用于python2.x的，但是如果要在python3.x下运行的话，需要将各文件中的print xxx修改为print(xxx)，注意print >>这种格式不变。

8. 编译工程

   catkin_make
   

   之后就可以按照官方的介绍运行launch脚本。

使用案例

download the repo and then put it in your ros package

catkin_make
source <repo_path>/devel/setup.bash

Single Robot Map Building

roslaunch gmm_map_python visualgmm_realsence.launch

Multi-robot Relative Pose Estimation

roslaunch gmm_map_python visualgmm_realsence_2robot.launch

原文：

• Dong, Haolin, et al. “MR-GMMapping: Communication Efficient Multi-Robot Mapping System via Gaussian Mixture Model.” IEEE Robotics and Automation Letters 7.2 (2022): 3294-3301.