Fisher线性判别算法原理及实现 MATLAB

Fisher线性判别算法原理及实现 MATLAB

一、Fisher判别器原理

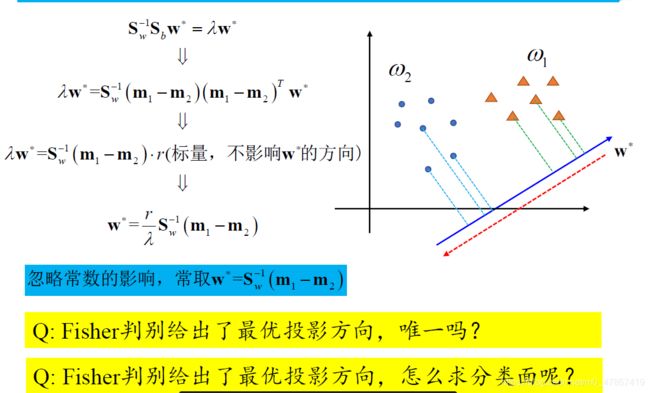
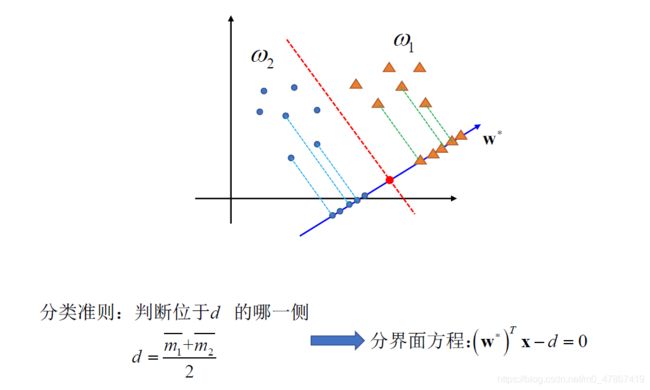
二、代码实现

clc;
close all;
clear;
%% 生成数据
rng(2020);   %指定一个种子
mu1 = [0 3];
sigma1 = [0.5 0; 
         0 0.5];
data1 = mvnrnd(mu1,sigma1,300); %生成一个300*2的矩阵，每一列的数据分别以0，3为均值，标准差都为0.5

rng(2021);  %指定一个种子
mu2 = [6 7];
sigma2 = [0.5 0; 
         0 0.5];
data2 = mvnrnd(mu2,sigma2,300); %生成一个300*2的矩阵，每一列的数据分别以6，7为均值，标准差都为0.5

% rng(2022);  %指定一个种子
% mu3 = [5 -5];
% sigma3 = [0.5 0; 
%          0 0.5];
% data3 = mvnrnd(mu3,sigma3,300); %生成一个300*2的矩阵，每一列的数据分别以5，-5为均值，标准差都为0.5

%% 
figure(1),plot(data1(:,1),data1(:,2),'r+');hold on;
plot(data2(:,1),data2(:,2),'b*');hold on;
% figure(3),plot(data3(:,1),data3(:,2),'m^');hold on;

%%
mu_1=mean(data1,1);  %求data1数据集的均值 mean是求每一列的均值
mu_2=mean(data2,1);  %求data2数据集的均值 mean是求每一列的均值
tmp=data1-repmat(mu_1,[size(data1,1),1]); %size(data1,1)返回data1第一维的大小 repmat将mu_1矩阵当成一个数，然后按后面的向量排列
S1=tmp'*tmp;   %计算出S1 下面的操作是一样的
tmp=data2-repmat(mu_2,[size(data2,1),1]);
S2=tmp'*tmp;
Sw=S1+S2;
w_star=Sw\(mu_1-mu_2)';  %这边直接用结论 注意这里的mu_1 mu_2是行向量，而PPT上的为列向量，所以多了个转置，实际上是一样的

%% Plot w_star
Data=[data1;data2]; %将两个数据集合并成一个数据集
[xmin,ymin]=min(Data,[],1); %返回每一列的最小值
[xmax,ymax]=max(Data,[],1); %返回每一列的最大值
X=xmin:0.1:xmax; %采样
k=w_star(2)/(w_star(1)+eps);%求出判别函数的斜率
plot(X,k*X-4,'k--'); %画出判别函数，-4只是上下平移，并不会影响到判别函数的方向，这里只是为了不让它穿过样本

%%
w_star=-w_star;  %反向
y1=data1*w_star; %计算data1中每一个样本的投影
y2=data2*w_star; %计算data2中每一个样本的投影
figure(2),plot(y1,zeros(length(y1)),'r+');hold on;
plot(y2,zeros(length(y2)),'b*');hold on; %横坐标是它们的投影，纵坐标取零是便于在一维中比较，可以发现两类样本分开了

%% Sw-1Sb特征值分解
Sb=(mu_1-mu_2)'*(mu_1-mu_2); %注意这里的mu_1 mu_2是行向量，而PPT上的为列向量，所以多了个转置，实际上是一样的
Tmp=Sw\Sb; % Jf矩阵
[V,D]=eig(Tmp); %V储存特征向量，D储存特征值，D是个对角阵，特征值储存在对角线上
D=diag(D); %提取出特征值行向量
[~,ind]=max(D);%最大特征值的序号
v=V(:,ind); %提取出与最大特征值对应的特征向量
k1=v(2)/(v(1)+eps);
figure(3),plot(data1(:,1),data1(:,2),'r+');hold on;
plot(data2(:,1),data2(:,2),'b*');hold on;
plot(X,k*X-4,'k--');hold on;
plot(X,k1*X-6,'m--'); %可以发现与第一种方法得到的结果是一样的

%% G(x)=w'x+w0
mu_y1=mean(y1); %计算data1数据投影的平均值
mu_y2=mean(y2); %计算data2数据投影的平均值
d=(mu_y1+mu_y2)/2; %d就是阈值
w0=-d;
figure(4),plot(data1(:,1),data1(:,2),'r+');hold on;
plot(data2(:,1),data2(:,2),'b*');hold on;
plot(X,k*X-4,'k--');hold on;
Y=(-w_star(1)*X-w0)/(w_star(2));%令G(x)=0解出y即可 注意x向量的第一个元素是横坐标，第二个元素是纵坐标
plot(X,Y,'m-');
axis equal;

三、实验结果

Figure 1:

Figure 2:

Figure 3:

Figure 4: