周志华 《机器学习初步》模型评估与选择
周志华 《机器学习初步》模型评估与选择
Datawhale2022年12月组队学习 ✌
文章目录
- 周志华 《机器学习初步》模型评估与选择
- 一.泛化能力
- 二.过拟合和欠拟合
-
- 泛化误差 VS 经验误差
- 过拟合 VS 欠拟合
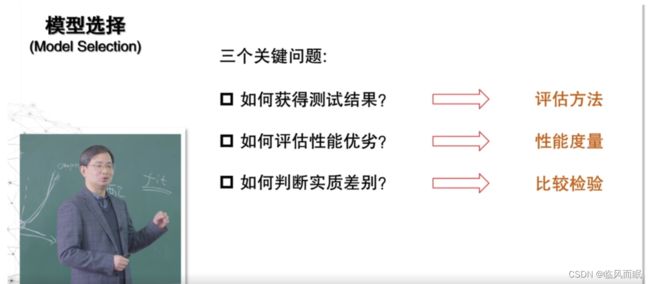
- 三.模型选择的三大问题
-
- 如何获得测试结果:评估方法
- 如何评估性能优劣:性能度量
- 如何判断实质差别:比较检验
- 四.评估方法
-
- 怎么样得到测试结果?
- 流出法
- k-折交叉验证法
- 自助法
- 五.调参与验证集
-
- 参数和超参数
- 验证集(validation set)
- 六.性能度量
-
- 回归(regression)任务常用均方误差
- 错误率
- 精度
- 查准率 vs 查全率
-
- 查准率 Precision
- 查全率 Recall
- F1度量
-
- 若对P/R有不同偏好
- 七.比较检验
-
- 常用方法
- 参考资料
一.泛化能力
-
我们当然是要学一个好的模型,但是什么模型好?这个问题不易回答。可以希望这个模型能够很好的适用于我们没有见过的样本,很好的适用于 unseen instance。
-
但是问题是什么叫”好“?可能有一些基本理解,比如错误率低,精度高,做 100 次如果能做对 99 次,这比做对 80 次要好。但这还是不易说出来。
-
比如我们考虑做推荐。一个淘宝上的电商,希望有一个机器学习的系统能把推荐做好。
- 比如说我手机上只看到 5 个东西,这 5 个东西推荐的都是我想要的,至于你第6个开始是不是好的,我不关心。
- 但是对另外一个人来说,在电脑上看,一下能看 15 个。要前 15 个都好才行。
- 这两个是完全不同的结果。
-
我们最希望的结果是一个东西对所有的标准都好,但这不太现实,太困难。所以我们要做的是搞清楚你要的到底是什么,我把你要的给你就好了,我不用关心对别人来说好不好。其实这和我们刚才说的 no free lunch 是同一个思想。
-
如果只关心前 5 个推荐是正确的,就不用去关心第 6 个开始推荐正不正确。
-
这实际上是做机器学习的人在看待问题的一个世界观或者方法论 O(∩_∩)O
很多做机器学习的人,会认为给你数据你就去跑,跑个算法,跑个结果,回来把结果给我,我说结果不好,你再给我一个新结果。其实不是这样的。
我们通常会要搞清楚你到底要什么,只有我把你到底要什么搞清楚了,我才知道我要给你什么。
-
模型评估和选择要解决这个问题,一方面我们要知道你到底要什么,另一方面我还要知道我给你的是不是你要的?这就是我们要解决的关键的背后的这两个问题。而这两个问题从技术上表现来看,它的表现形式可能又要拆解为具体的进几步要讨论的技术问题。
-
-
总的来说,一个模型的泛化能力强,就是对新的没有见过的数据的处理能力强。
-
但是问题是,就算我知道你想要的是什么,我手上没有没见过的数据,我怎么知道我给你的东西恰恰是在没见过的数据上表现的特别好,真的是你想要的呢?
-
要引进几个概念
嘶,不知道这里课程是不是连续的,听视频有种戛然而止的感觉…
-
二.过拟合和欠拟合
泛化误差 VS 经验误差

-
泛化误差:在”未来“样本上的误差
- 我们需要的是模型在未来的东西上表现的好叫泛化能力(generalization ability)。这是我们机器学习所考虑的核心。
- 绝对不是只在你给我的训练数据上表现的好。如果只要这样,我什么都不用做,我把数据全存起来就好了。一定是要在新的、没见过的东西上表现的好,叫泛化性能,刻画它的误差叫泛化误差。
- 我们需要的是模型在未来的东西上表现的好叫泛化能力(generalization ability)。这是我们机器学习所考虑的核心。
-
经验误差(训练误差):在训练集上的误差
- 已经给我的数据,可以叫训练数据,也可以叫经验数据。
-
比如我拿到这么一个数据集,有 4 条样本,全做对了,我的训练误差就是0,训练集精度百分之百。但是这时候泛化误差是多少并我不知道。
-
我们能控制的是训练集上的结果。但是我们想要的是未来的结果。**我们一定要在这两者之间找到某种联系。**如果彻底没有联系,机器学习学科就不用存在了。因为你做出来的结果和未来完全不发生关系,你根本什么都不用做了。
-
其实也就是未来的数据和现在的数据符合同样的规律。这时候才能指望做一个好的机器学习模型。
- 我们必须在这个假设下工作,新数据和已有数据符合同一个规律。
-
我怎么知道我根据已有数据找出来模型是真正的把规律发掘出来了?
-
我们能控制经验误差,那么是不是在训练数据上误差最小了,我就真正的把隐含的规律找出来了?
To put it another way,经验误差(训练误差)是不是越小越好?答案是NO!
为什么?这是我们在机器学习中会出现的一个问题,叫 overfitting,过拟合,有的地方把它翻译成过配
-
过拟合 VS 欠拟合
-
现在假设有这么一个训练数据集:上图这两片树叶。现在给一个算法,让它学一个模型,这个模型要做到今后再给一个东西,它判断是不是树叶。
-
现在训练出一个模型,这个模型能力特别强,它甚至发现有锯齿。然后给它一个新样本,它说这不是树叶,因为没有锯齿。 但是我们看图显然知道这是树叶, 这就是发生了overfitting,它把训练数据里面的特性学出来了,而这个特性恰好还不是一般规律。
-
比如我们现在拿到这两片训练树叶,正好都有锯齿,这是训练集所满足的一个特性,特有的性质。而这个特有的性质不是一般规律。但是我们这个模型错误的把它当成一般规律了,认为所有的树叶都要有锯齿,他就做错了,这就叫过拟合。
-
那么欠拟合是啥,重要的东西没学出来。比如它发现这两个树叶都是绿色的,以后,我们拿一个绿色的东西,它认为这就是树叶,这就叫欠拟合,underfitting。
-
一个事情,一开始我们还什么都没学到,这就是 underfitting,你会犯错误。
但有时候你学到了太多,学到了你不该学的东西,这就是overfitting。感觉老师讲的好清楚 orz
-
老师提到了那个曲线
周老师画的这个应该是对应下图的total error和bias
想到了之前看过的这个图
-
一开始我们还没学到什么东西,误差会非常大,左端是underfitting。随着学习的进步,我们性能会逐渐变好,误差逐渐下降,但是当我们学到一定程度之后,再继续学下去的时候,就有可能是把训练数据里面的特性不该学的东西学出来了,这时候模型就会变坏。到右端发生的就是 overfitting。这是在未来的数据上的表现
-
而在训练数据上表现是什么?很可能是训练误差一直在下降。
- 训练误差一直在下降,但是在测试,考虑未来的时候,一开始是在下降,到了后来上升了。**这告诉我们训练误差并不是越小越好。**当训练误差太小的时候,可能已经把不该学的东西学进去了。
-
我们真正应该学出来的是什么?是一个理想的平衡点。
wow,从计算理论的角度来解释好棒诶!
-
但是没有完美的解决方案,也不指望有完美的解决方案。如果有完美的解决方案,也就意味着这个问题我能把确定最好的模型给你了。
这个其实就是把一个甚至比 NP 问题还困难的问题。在多项式时间里面,我这个算法跑出一个结果是能够把最好的结果给你。其实你已经构造性地证明了 p 等于NP,甚至更难的问题。所以只要我们相信 p 和n p 是不等的,就不要指望有完美的解决方案。
-
所以机器学习始终在和这件事做斗争。不同的算法在用不同的机制跟这件事做斗争。
-
-
换一个角度来想,如果 overfitting 这个现象不存在,机器学习学科也不需要存在了。你有一个训练集,你就找一个模型,在训练集上做到 0 误差就 OK 了,这是最好的。这件事情非常简单,你不需要再专门有一个学问要来研究怎么去做到这件事。所以overfitting 是机器学习里面的核心内容。从这个角度来看,可以认为所有的算法,所有的技术都是在缓解,而不是解决overfitting。
-
学习具体算法的时候,就应该思考几个问题
- 这个算法靠什么来缓解overfitting?
- 它缓解 overfitting 的策略在什么时候会失效?
如果把这个两个问题搞明白。就能明白这个算法应该在什么时候用,什么时候不该用

三.模型选择的三大问题
如何获得测试结果:评估方法
-
我们拿到一个模型之后,怎么评估出它在未来可能会怎么样?
如何评估性能优劣:性能度量
感觉这些除了对机器学习本身,对整个人思维也很有启发哈哈哈
- 做100次,有99次做对是不是就很好了?不一定
- 比如信用卡欺诈检测问题,100万次交易里面可能只有 10 次是欺诈。现在做一个模型,任给一个东西,你都说不是欺诈,它的精度已经99.9%。
- 但是这个模型是你要的吗?绝对不是你要的,因为它一个欺诈都检测不出来
- 我们必须理解我们对一个任务可能有哪些刻画的标准
如何判断实质差别:比较检验
为了说明模型在统计意义上表现好,我们最需要考虑**比较检验**
- 我们在机器学习里面做的是概率近似,我得到的模型都是概率意义上好。
- 但是,存在这种情况:它这一次做的特别好,大多数情况它很糟糕。但是我们就因为这次做的很好就很信任它,结果真正用起来恰好是大多数情况,那就很糟糕。所以我们还要引入一些比较检验来说在统计意义上这个模型是不是好的。
- 整个第二章我们要解决的就是上面这三个具体技术问题。而这三个技术具体技术问题解决之后,就知道了”我们要知道你到底想要什么样的结果。我要知道我怎么样给你这个结果“。
- 上面这三个技术是”有什么“(比如书上有10种度量),绝对不是包含所有的 可能有什么 ,而在未来要面临的是”可能有什么“,很可能你要发明出一些东西来,而发明这些东西它的思路是什么就可以从这些作为原始的套路把衍生出来。
四.评估方法
怎么样得到测试结果?
![]()
-
我们只有用户给我们的训练数据,但是我们现在要判断模型在未来会怎么样,怎么做? 关键就是怎样获得”测试集“
-
测试集是代表了未来我们没见过的东西,训练的时候没见过的东西。
-
首先要知道测试集应该和训练集互斥。
我训练的时候给了你 30 道题,测试的时候从里面挑 10 道题,你测试出来的结果一定是个对你的能力的过高估计,这不是个恰当的估计,所以一定是和你应该是完全不一样,这时候我才真正能客观的估计你的结果。
-
但是问题来了,我手上只有一个数据集,我怎么办?常见的方法有这 3 种。
- 流出法,hold-out
- 交叉验证,cross validation,简称叫cv
- 自助法,bootstrap。
流出法
![]()
假设这是 100 个样本,割成两部分,左边这一部分用来训练,右边那部分用来测试。比如给我 100 个数据,我拿 80 个训练模型,我拿 20 个来测试模型表现的怎么样。这就是最简单的流出法。
-
流出法的注意点
-
保证数据分布的一致性(例如:分层采样)
- 比如做两类分类 yes or no,好瓜和坏瓜, 50 个好瓜 50 和坏瓜。
- 训练的时候,80 个瓜,应该有 40 个好的,40个坏的,另外 20 个测试的,应该有 10 个好的,10个坏的。
- 不能这样:训练集 80 个, 50 个好的, 30 个坏的。测试集20 个全是坏的,测出来的也不对了。
- 这样一种根据类别的均匀的分布的采样,这个叫分层采样, stratified sampling
- 比如做两类分类 yes or no,好瓜和坏瓜, 50 个好瓜 50 和坏瓜。
-
多次重复划分(例如:100次随即划分)
- 拿 100 个样本,切一刀,拿 20 个来测试,每次到底怎么切的,会有很大影响
- 比如取最前面20个,取最后面20个?信谁?谁都不要信。做 100 次,求个平均值。
- 所以通常我们做这种 hold out 的测试,一定是要做 100 次的,这样才能保证随机的样本的切分导致造成的影响被平均掉。否则性能可能是由于切分造成的。
- 这部分训练和另一部分部分训练,得到的模型本来就不一样,更不要说拿这个测试和另一个个测试也会导致不一样。
- 我们要把数据切分造成的影响去掉。
-
测试集不能太大,也不能太小。(比如五分之一到三分之一)

-
要理解这种 hold out 测试的缺陷
- 假设这 100 个样本是完整的数据。把训练出来的模型叫做 M 100 M_{100} M100,我们希望判断它未来的性能怎么样,我们把它叫做 e r r 100 err_{100} err100, M 100 M_{100} M100能得到,但是 e r r 100 err_{100} err100是得不到的
- 现在把它一切,假设训练是80,测试是20,我们做的 M 80 M_{80} M80你要注意,已经不是 M 100 M_{100} M100了。用20对80的测试来对 e r r 80 err_{80} err80 做一个估计,并用 e r r 80 err_{80} err80来近似 e r r 100 err_{100} err100
- 可以发现问题了!如果测试数据用的太多,其实你测的这个模型已经不是我最后真正用的模型了。我最后用的应该是拿着 100 个样本训练出来的模型,结果你弄了个 80 个样本训练出来的模型。算法在80个训练出来的模型好了,但是有可能 80 个它好了,90个另外一个算法更好。所以我们是在用模型在近似,它近似能力肯定是随着训练集变小,近似能力差。所以训练集不能太小,越小对他的逼近能力就越差。
- 另一方面,我们要测出这个东西来。这个东西测的准不准,其实和测试数据有关系,测试数据越少,测的越不准,多一点才能测得准一点。但是训练集和测试集都想更大,这是个不可调和的矛盾。所以一般来说,我们只能用经验上的做法,用 20% 或者 1/3 的数据来做测试集,其他的用来做训练集。
-
-
![]()
- 此时,假设我们现在有两个算法L1和L2,在这上面做了之后,我们发现 e r r ~ 80 ( L 1 ) \widetilde{err}_{80}(L1) err 80(L1) 小于 e r r ~ 80 ( L 2 ) \widetilde{err}_{80}(L2) err 80(L2),这时候我们怎么办?
- 我们就 take 了 L1 算法,我们认为 L1 算法在这上面是好的,是不是直接把这个模型给用户就算了?非也
- 确定后,应该把所有的数据合起来,再来用 L1 训练一下,把这时候得到的模型给用户。
- 所以我们划分数据,训练测试的过程,实际上只是在选起到一个选择的作用。选定了之后,应该把整个数据合起来,再训练一下模型,再提交给用户。这是 hold out 测试,比较简单。
k-折交叉验证法
-
hold out 测试还有一个问题。
-
有数据,可能训练的时候永远没用上,或者测试的时候永远没用上。因为每次都是随机挑20%,假设 1/5 来做测试集,就算挑 100 次,也有可能有数据漏掉。也有可能数据永远没出现在测试数据集里面。而我未来处理的问题里面,这样的问题其实挺重要的。而这样的问题没有测过,有可能未来会很糟糕。
这就好比我们这门课上有 100 个知识点,有 2 个知识点其实挺重要的,以后你们经常用。但是我每次随机猜 10 个,每次猜随机猜 20 个,那两个知识点总归没有考过你们,没考过你们,所以你们在那两个知识点上可能性能非常糟糕,最后得到的是一个过于乐观的估计,最后解决实际问题的时候,发现那两个知识点,原来你们一塌糊涂就有问题了。我们最理想的应该是什么?所有的知识点我都已经全面的检查过你们。希望训练集里面的所有数据,实际上模型性能怎么样都考察过。
-
k-折交叉验证法则可以把上面的问题解决掉
- 折在英文里面是fold,有时fold 翻译为倍
- 假设现在有 100 个数据,们把它分成完全一样大的 10 个子集。第一个就是数据1-10,后面是11-20,21-30,最后这是第91-100。
- 做 10 次测试,每次测试把其中的一个子集拿出来做测试集,剩下的 9 个做训练集。
- 这样轮转一次正好要做 10 次,这样做了之后,整个数据集里面的每一个数据都在测试集里面用过了
- 这叫10-折交叉验证或者 ten fold cross validation。这样做的结果,我们把它平均一下就返回结果了。
-
但是这里面还有一个问题,划分这 10 个子集,不同的切分可能也会导致数据有变化,而这个变化可能会影响估计的性能。
- 所以我们把切分再随机做 10 次,这样做下来就叫 10*10 的交叉验证。所以其实也是做 100 次实验。和刚才 100 次 hold out 流出法一样,也是做 100 次实验。
- 用刚才的说法,假设 100 个样本,现在是用 M90 来逼近M100,肯定比刚才的M80 逼近 M100 要准一点。
- 如果做到极致,每次就留一个样本来测试,也是所有样本都测试过一遍,假设有 100 个。其实就是在用 M99 的估计来逼近 M100 的估计。
- 这样的做法是有的,这种做法就叫留一法,简称 Loo, leave-one-out
- 所有的数据我们每次留一个来测试,剩下 99 个训练,这样训练的模型和最后用所有数据得到的模型应该是高度相似。这样做是不是就更准?不是的。
- 永远记住 no free lunch 。这样做了之后,每次测试的时候只有一个样本,虽然训练的模型和真正要得到模型很近似的,但是测试可能会有偏差
- 没有任何一个评估测试的方法是最好的,它都有它合适的时候,有它不合适的时候
- 所有的数据我们每次留一个来测试,剩下 99 个训练,这样训练的模型和最后用所有数据得到的模型应该是高度相似。这样做是不是就更准?不是的。
自助法
![]()
-
有没有办法在训练的时候就能训练出一个 M100 来,同时还留出一些样本,在未来能够做测试?这种办法就来解决这个问题。
-
自助法的基础是依赖于有放回采样(可重复采样)
-
我们想象一个盒子,放了 10 个球,每次摸一个球,再把这个球放回去,下次再取一个球,有的球会多次出现,有的球根本没取到。
-
但是不管怎么说,原来有 10 个球,现在还可以取 10 个球出来。只不过有的是重复的,有的样本出现了好几次。但是以这种方式,原来假设是 100 个数据做模型,现在就能采样出一个数据集来用 100 个样本做模型,同时里面没有出现的数据,就可以留出来做测试。
-
没有出现的数据大概会有多少?
- 我们可以做这么一个估计,非常简单的估计。
- m 个样本,取 m 次,它不出现的可能性是1-1/m 。
- 取了m次,就是m次幂, 非常大的时候,就是1/e,也就是大概有 36.8% 的数据在取出来的集合里面没有出现。现在我们就能用没有出现的这部分来做测试集。
- 这样一个测试叫 out-of-bag estimation(包外估计)。
- 原来的 100 个,闭着眼睛可重复采样取 100 个,训练了 100 个做的模型,用原来的没取到的这些来测试。
-
这样一种技术它的缺陷是什么?
-
最重大的缺陷就是它改变了训练数据的分布
-
我们应该是用这样的一个训练数据的分布结果(slide左图)。结果它用这样来做训练数据了(slide右图)。本来我们这 10 个样本,这 10 个球应该同等重要,结果做的模型可能认为某球更重要。模型在这上面可能得到了一个高估
-
但是有时候如果我们认为训练分布它稍微变一点,不太重要的时候,这种技术很好。而且有时候数据量不够的时候用也挺好。所以一定要考虑使用场景
-
-
-
嘶,低级错误
五.调参与验证集

参数和超参数
- 我们有时候把算法本身的参数叫超参数
- 模型的参数,我们把它叫参数。这个参数是要算法去学的,超参数是人去设的。
- 比如我们有一个算法是用多项式函数去逼近数据,比如二次的 a x 2 + b x + c a x^2+ b x + c ax2+bx+c,三次的 a x 3 + . . . ax^3+... ax3+...
- 我现在有一个参数说你的次数是多少,我现在请用户来提供,你说 2 我就用2,你说 3 我就用3。这个次数就是一个超参数(super parameter),由用户来提供。这个提供之后,如果是用2,我就用二次曲线。
- 拟合数据过程中算法要确定的是a、b、c,这就是算法要确定模型的参数,我们直接就把它叫参数(parameter)
- 超参数和参数,其实本质上它都是一种参数。调参数本身就是在做一个模型选择,可以认为每一个模型就是参数对算法,对数据的一种实例化。
- 在学习过程中, a 是100, b 是10, c 是1,这就是一个模型了,这其实就是确定了参数了。而这个模型不好,最后学到的a 是2, b 是3, c 是0 才好。其实就是很多种参数实例化的模型,在对模型在做选择,而在做模型选择的时候,其实就是通过调参数,每次调参数,就在做一种评估,现在模型好不好,可以把评估方法用上。
- 比如训练神经网络的时候,训练到多少轮停,其实每一轮也都在评估当前神经网络性能是怎么样,下面一轮和现在性能差不多,就不往下训练了。其实每一轮都在产生一个模型。
- 所以调参数就是在进行模型选择,选不同的算法也是在进行模型选择。
- 我们用模型选择这个词,其实是覆盖了机器学习中很多的变量确定的过程。
- 算法本身也可以认为是一个变量(用 A 算法还是 B 算法)
- 算法的参数也是一种变量。
- 模型选择很广泛。任何机器学习中的这种变的东西,我们在确定确定它们的过程,其实都是模型选择的过程。
验证集(validation set)
- 验证集专门用来调参数,它是训练集中专门留出来用来调参数的部分。
- 其实这个集合也是一种测试集,只不过这个测试的结果是为了看我们参数怎么样测评才是好的
- 最后我们如果参数选定之后,我们要把训练集+验证集 合起来,这个模型再放到测试集上去测试,才得到它的性能。
- 初学者容易犯的错误:直接把最后用来评估性能的集合来调参数。测试集一定要是在训练过程中没有用到的,而调参数的过程也是训练的一部分,所以调参数的数据应该从训练数据中来,而不是从测试数据中来。
六.性能度量
同一个算法对同一个数据得出来的模型,对 a 好,可能对 b 不一定好,因为目标可能不一样。
回归(regression)任务常用均方误差
E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f ; D)=\frac{1}{m} \sum_{i=1}^{m}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2} E(f;D)=m1i=1∑m(f(xi)−yi)2
-
f(x)是hypothesis, y 是我们的 ground truth,它们的差取一个平方,对所有样本 m 取一个均值,这就叫均方误差(有时也叫二次误差,平方误差),有时候也把它叫做,都是一回事,甚至有时候我们前面加个 1/2 都是一样的
-
前面加上1/2方便求导计算

错误率
- 分类这样的任务,最简单的就是错误率
- 有 m 个样本,有多少次做的ground-truth 不一样,每做一次,做错一次就扣 1 分
E ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i ) \begin{aligned} E(f ; D)= & \frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) \\ \end{aligned} E(f;D)=m1i=1∑mI(f(xi)=yi)
精度
- 精度是1减错误率
acc ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i ) = 1 − E ( f ; D ) . \begin{aligned} \operatorname{acc}(f ; D) & =\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right)=y_{i}\right) \\ & =1-E(f ; D) .\end{aligned} acc(f;D)=m1i=1∑mI(f(xi)=yi)=1−E(f;D).
查准率 vs 查全率
- 对分类结果,我们可以得到一个混淆矩阵。大家看一看表。我们这个方向是叫预测结果,这个方向是真实情况。
- true positive 是真正例:预测结果认为它是正例,真实结果也是正例,用 TP 表示。
- false positive 是假正例:预测结果是是正例,实际上你是反例,用FP表示
- false negative 是假反例:预测是反例,真实结果上是正例,用FN表示
- true negative 是真反例:真实结果是反例,预测出来也是反例,用TN表示
- 矩阵的正对角线是正确预测,副对角线是错误预测
查准率 Precision
P = T P T P + F P P=\frac{T P}{T P+F P} P=TP+FPTP
- 它是在所有预测出来的 positive 里面true positive 的占比
- 回到,预测出来 10 个是好瓜,这 10 个好瓜里面,真正的好瓜有多少,这个叫查准率(Precision),
- 有的地方会翻译成精度,但是这里为了和前面acc区分,翻译为查准率
查全率 Recall
P = T P T P + F N P=\frac{T P}{T P+F N} P=TP+FNTP
-
在所有的正样本里面,有多少被找出来了?你看出 positive 是正样本里面你预测为正的。
-
可以这样理解 precision和recall
-
有 100 个西瓜,现在预测出有 10 个是好的
- 这 10 个里面有多少个真正是好的?这就是查准率
- 原来 100 个里面有 20 个是好的,只预测给出了我 10 个,查全率就只有50%
-
如果第一个算法在 p 上更好,第二个算法在 r 上更好。到底谁好?我们把这两个东西合在一起,可以得到一些指标
F1度量
F 1 = 2 × P × R P + R = 2 × T P 样例总数 + T P − T N \begin{aligned} F 1 & =\frac{2 \times P \times R}{P+R} \quad \\ & =\frac{2 \times T P}{\text { 样例总数 }+T P-T N}\end{aligned} F1=P+R2×P×R= 样例总数 +TP−TN2×TP
1 F 1 = 1 2 ⋅ ( 1 P + 1 R ) \frac{1}{F 1}=\frac{1}{2} \cdot\left(\frac{1}{P}+\frac{1}{R}\right) F11=21⋅(P1+R1)
- 实际上是 P 和 R 的一个调和平均。(这个比几何平均和算术平均好,调和平均能使得较小的值不那么容易被忽视)
若对P/R有不同偏好
- 如果我对查准率,查全率还有不同的偏好,可以引入权重
F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R β > 1 时 查 全 率 有 更 大 影 响 ; β < 1 时 查 准 率 有 更 大 影 响 F_{\beta}=\frac{\left(1+\beta^{2}\right) \times P \times R}{\left(\beta^{2} \times P\right)+R} \quad \\\beta>1 时查全率有更大影响; \beta<1 时查准率有更大影响 Fβ=(β2×P)+R(1+β2)×P×Rβ>1时查全率有更大影响;β<1时查准率有更大影响
1 F β = 1 1 + β 2 ⋅ ( 1 P + β 2 R ) \frac{1}{F_{\beta}}=\frac{1}{1+\beta^{2}} \cdot\left(\frac{1}{P}+\frac{\beta^{2}}{R}\right)\\ Fβ1=1+β21⋅(P1+Rβ2)
- 这样有助于做取舍。
- 比如查准率更重要,但是查准率比查询率重要性不超过它的两倍,大概 1.5 倍那么重要。那可以设一个 β \beta β,用这个来做一个balance,这是一种把这两者考虑在一起的一种均衡的办法。
七.比较检验

- 我们在某种度量之后得到评估结果了。能不能把评估结果值直接用来判断 ? 通常是不行的。
- 因为测试性能不等于泛化性能
- 泛化指的是未来,但是未来的数据我没有,我只是拿给定的集合里面判断,这个是测试性能,这两者本来就不一样。
- 测试性能会随着测试集的变化而变化。
- 同样是 100 个样本,这次拿这 10 个测试 90 个训练,和下次拿这 10 个测试这 90 个训练,它结果可能是不一样的。到底信哪个?这又是一个问题。
- 很多机器学习算法本身就有一定的随机性
- 比如现在最流行的深度神经网络,初始化结果不一样,性能可能就非常的不一样。
- 因为测试性能不等于泛化性能
- 所以有这么多原因都导致我们不能简单的通过一个值来判断。
- 机器学习一定不是在找确定的最优的,机器学习找的都是概率近似正确,以很大的可能性得到一个很可能很好的模型。既然都是概率并且是可能,就不能说一次确定性的比较就决定一切。所以在这个时候我们通常要依赖于数理统计提供的假设检验的办法
常用方法
![]()
-
我们通常要做一个假设, 说A 算法和 B 算法性能是不是一样,我们来看他们的实验结果。这就是我们的观察。我们来判断能不能把刚才的假设拒绝掉。如果拒绝了,那就说明不一样,如果没拒绝,那就说明性能是一样的。
下面老师举的例子这里没有记录
参考资料
-
西瓜书
-
MOOC