机器学习:房价预测项目实战

        作为机器学习刚入门门都没入的小白，学了理论总有一种有力使不出的赶脚，就想拿一些项目去练练手，而房价预测作为kaggle入门级别的项目，又是最经典的项目，于是就拿来试试啦。

 注：本文的数据集链接来源于kaggle

https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques/data

参照的是这位大佬的思路

Comprehensive data exploration with Python | Kaggle

分割线

---

目录

目录

开局：读取文件与可视化

可视化

相关性分析

散点图

箱型图

直方图

缺失值处理

离群点(异常值)

统计学分析

划分数据集和训练

---

开局：读取文件与可视化

可视化

相关性分析

散点图

直方图

缺失值处理

离群点(异常值)

统计学分析

---

开局：读取文件与可视化

既然面对大量的数据，那么第一步自然是导入数据并可视化了

# 训练数据
data=pd.read_csv(train_path)
# 提交结果的数据
test_data=pd.read_csv(test_path)

        这是将数据的信息打印出来后的结果，可以看到RangeIndex共有1460条，也就是说明共有1460条数据，数据量看起来还听小的(比起商业数据或者真正项目的数据来说)

        不过看到有81列数据，这就让我们头疼了，需要把81维的数据全部提取出来作为特征吗？其实并不需要。

        因为许多维度表示的信息是重复的，也有些信息是非必要的，就像一般人买房时会考虑到家里泳池的大小或者买未交付的房子吗，显然不会喽，所以我们仅仅需要关注那些我们需要关注的信息就好了，这样能够大大降低特征表示的难度和计算机的计算量。

可视化

         怎么找到我们需要关注的特征？这时候就需要可视化登场了。首先，我先提取了那些数值化(numerical)的列，这些才能够在图上显示。

# 数值化的列名
columns_numerical={i:data[i].dtype for i in data.columns if data[i].dtype!=object}

        既然是要预测房价，首先想到的是看看那些变量与房价有较高的相关性，在这里我们不妨采用plot绘图，当然，因为数值化的列实在太多了，子图形式呈现的化根本看不清，所以只能一张一张图来展示了。

for j in columns_numerical:
    plt.scatter(data[j],data['SalePrice'],label=j)
    plt.xlabel(j)
    plt.ylabel('SalePrice')
    plt.legend()
    plt.show()

因为数量太多，就不一个个展示了，部分可视化的图片如下：

        从这里可以看到一些变量和房价还是有相关性的，太好了！至少我们知道哪些变量可以称之为我们需要关注的变量的，但是这样一个一个去看图，看到下个图就把上个图的样子给忘了，根本记不住谁和房价相关性强，还是不利于分析，怎么办？

相关性分析

        不要忘记了，我们还有相关系数这一法宝呢，对数值列的特征进行相关系数分析：

corr=data.corr()
plt.figure(figsize=(12,8))
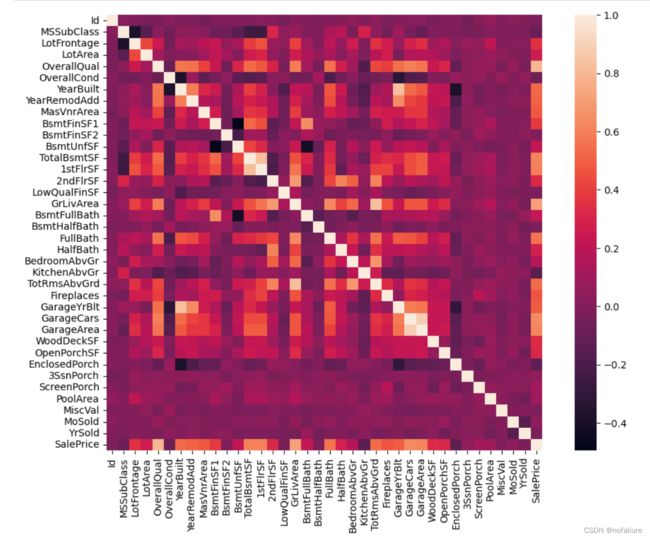
sns.heatmap(corr,square=True,annot=False)
plt.show()

显示的效果：

        好像我们可以看到一些相关系数高的变量了，像‘YearBuilt’和'Garagecars'，但一个个去看有点太反人类了(如果在每个小块上都标注相关系数的值更看不清了)，看来数据的维度还是太高了。

但是我们最关心的还是房价和其他变量之间的关系，例如车库面积和房子类型，是商品房还是合租房这个我们并不关心，这就需要我们选出与房价相关性最高的几个变量：

#saleprice correlation matrix
k = 10 #number of variables for heatmap
cols = corr.nlargest(k, 'SalePrice')['SalePrice'].index
corr_10=corr.loc[cols,cols]

        在这里我们选择十个就好，当然你也可以不选择十个，十五个也可以，但要考虑是否一张图表可以显示完，也可以少一点，比如七个八个，但是也不能太少，否则有可能忽略掉‘重要’变量。

plt.figure(figsize=(12,8))
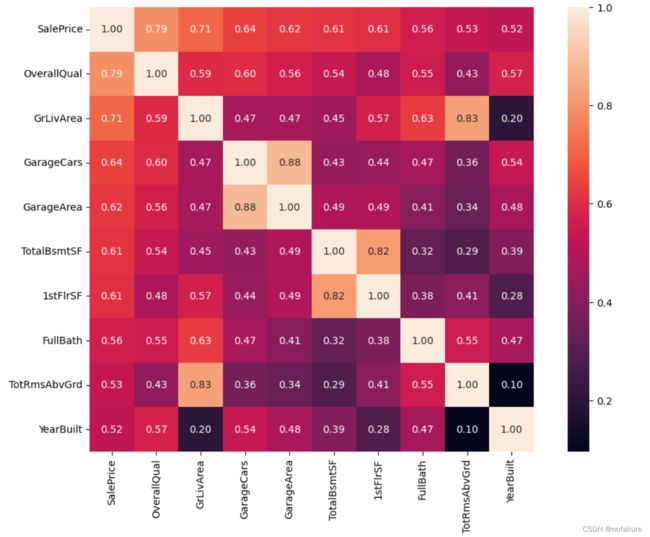
sns.heatmap(corr_10,annot=True,square=True,fmt='.2f', annot_kws={'size': 10},yticklabels=cols.values, xticklabels=cols.values)
plt.show()

         嗯，这个时候的热图就好看多了嘛，是不是有点降维打击的感觉了，话说最近三体动画也开播了，作为科技爱好者死肥宅的我当然要去看了，三体文明就是从比人类更高维的世界企图毁灭人类，殖民地球，其中的智子，以纳米级的能力居然干涉了地球粒子对撞实验，阻止了地球在微观世界科技的进步.....，扯远了，废话少说，开始分析！

        其中有一些变量其实是重复的，'1stFlrSF'(一层面积)和房屋面积其实表示信息差不多，'GarageArea'和'GarageCar'表示重复,类似...，所以我们把这几个变量当中主要的部分留下来，次要或者重复的部分去除，留下的我们可以称为'主要变量'。

        那么，我们留下来的主要变量主要是以下几个，其中房价是我们需要关注的因变量的值，所以在这里选择留下。

散点图

 绘制房价和主要变量之间的散点图：

data_copy=data[main_factor]
plt.figure(figsize=(12,8))
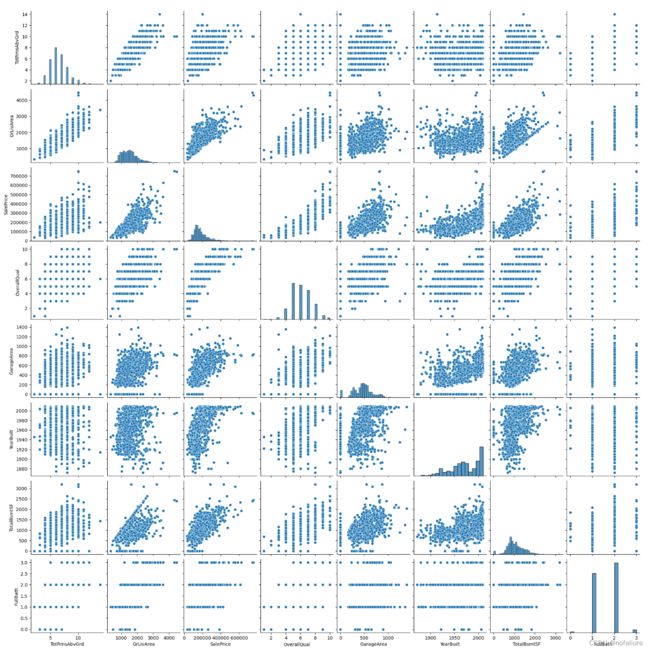
sns.pairplot(data_copy, size = 2.5)
plt.show()

        这样子图就好看多了嘛，可以看到房价和居住面积有着很大的线性相关性，其他的变量或多或少也有相关性，与‘YearBuilt’(建造年份)有着稍微不明显的指数关系，与'TotalBsmtSF'(地下室面积)有着类似指数关系。我们可以从这几个变量入手分析。

箱型图

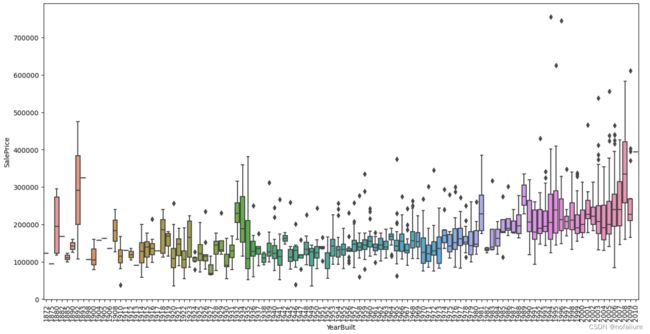
 销售价格和建造年的相关性

 销售价格和‘OverallQual’的相关性

直方图

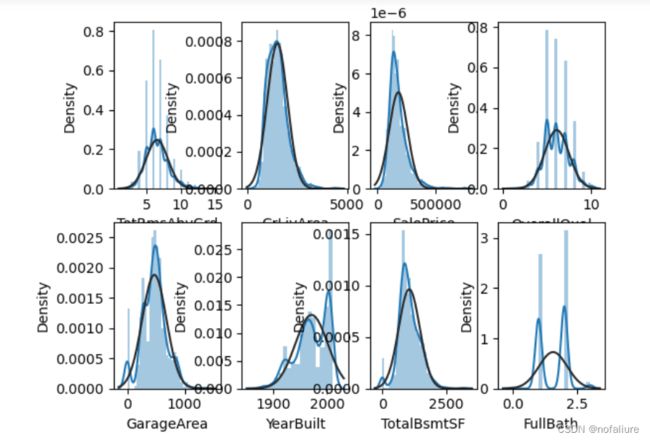
        不过既然要分析数据间的统计关系，那么散点图肯定是不够的，这个时候就需要我们拿出统计学的大杀器——直方图，直方图可以很好地观察到数据的分布情况。部分的可视化情况如下所示：

for index,column in enumerate(main_factor):
    ax=plt.subplot(2,4,index+1)
    # 以正态分布作基准
    sns.distplot(data[column], fit=norm)
plt.figure(figsize=(12,4))
plt.show()

        可以看到变量大部分还是符合正态分布的，只不过有的变量存在尖峰和倾斜度，需要调整使其符合正态分布。Comprehensive data exploration with Python | Kaggle该文中提到了调整的方法，在这里就不赘述了。

缺失值处理

total=data.isnull().sum().sort_values(ascending=False)
percentage=data.isnull().sum().sort_values(ascending=False)/data.isnull().count()
percentage.sort_values(ascending=False,inplace=True)
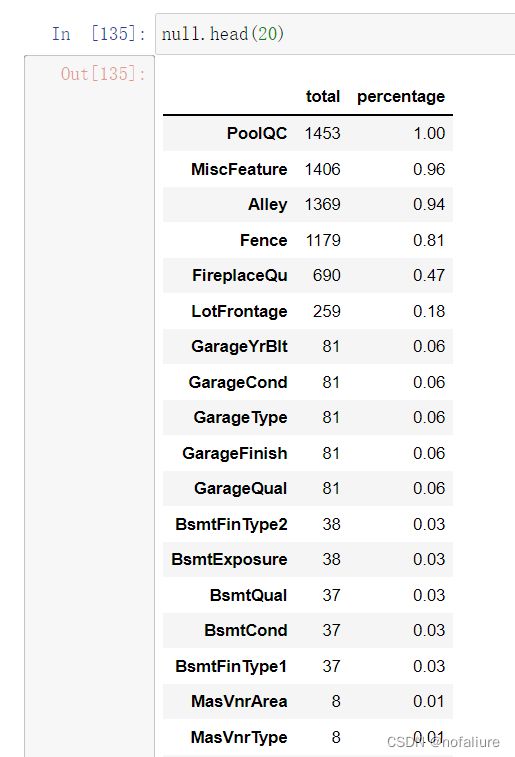
null=pd.concat([total,percentage],axis=1,keys=['total','percentage'])

        可以看到其中的缺失值还是很多的，甚至有一项都达到了100%,所以这些数据大多是属于无意义的数据，大多数情况下认为缺失值达到15%时就可以drop掉。那么那些缺失值并不是很多的数据一般来说是不删除而采取补全缺失值措施的，但在这里由于Garagexxx系列的数据和GarageCar等信息重复，可以剔除。类似，Bsmtxxx系列数据亦可以剔除。

# 剔除缺失值
data.drop(null[null['total']>1].index,axis=1,inplace=True)
data.drop(data[data['Electrical'].isnull()].index,inplace=True)
data.isnull().sum().sum()

out:0

离群点(异常值)

        我们知道，有时候离群点对于数据分布的影响很大，甚至可以以一己之力拉动数据的平均值和标准差，这些离群点明显是不符合两个变量之间的关系的，所以对数据的分布会带来较大的影响，这就需要我们去除离群点。

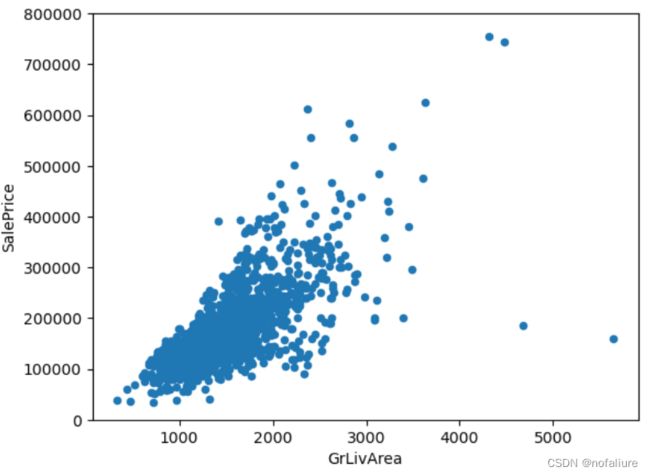
先看这张图

        可以看出GrLivArea和SalePrice成一种扇状分布，那么明显可以看到GrLivArea偏大时但房价却不变，这就好似你买了一个农村里面200平米的房子(有可能是通过亲戚间的关系拿到的)和上海城市里面30平米的房子花了差不多的价格，但这种情况却是应该排除的，因为在图上看来这样的例子太少了，对数据的分布不具有代表性，反而会扰乱数据的分布。

# 去除掉不合理的'GrLivArea'
data.drop(data['GrLivArea'].sort_values(ascending=False)[:2].index,inplace=True)
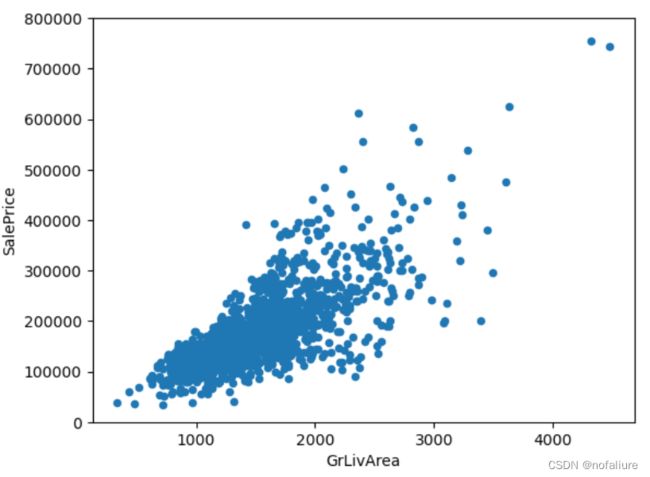
data[['SalePrice','GrLivArea']].plot.scatter(x='GrLivArea', y='SalePrice', ylim=(0,800000))
plt.show()

 这张图看起来就好多了，至少大家都是分布在一个扇状区域内。

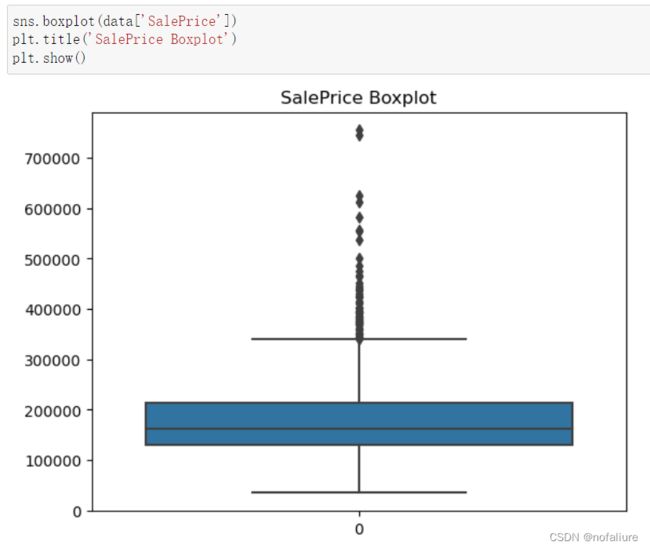
其实上面提到的箱型图也能够反映出数据是否存在离群点

        就像这张图反映了价格当中存在很高的价格，也就是价格当中的异常值，但是其实这只是对于数据分布来说异常，大多数的房价还是处于320000以下的，但是上面的离群点是不能排除的，就像你不能否定有富豪一手买下几亿别墅一样。所以说在这里我们不删除这些价格较高的‘离群点’。

        对于每个项目来说，不同的异常值处理也是不一样的，异常值是否需要排除是需要我们根据项目的需要和实际数据的分布情况来排除的。就像股票的涨跌，有可能一下子暴涨或者暴跌，对一个比较稳定的股票来说，这种情况是很少的，即便我们分析的时候碰到了也可以将其去除，但是如果说这支股票可能本身就不稳定，一直出现暴涨暴跌的情况，这下是不是排除掉这些‘异常值’就不合理了。

统计学分析

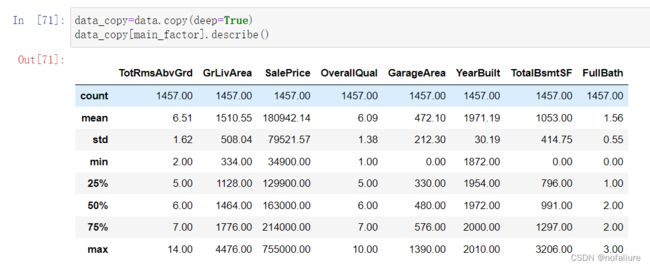
对上文我们分析留下的那些主要变量先describe一下：

        有些信息还是有用的，像价格、居住面积的均值和标准差，一定程度上反应大家更喜欢多大的房子和大多数人买房时可以接受的价格。

        上文提到了这些主要变量的分布情况，可以看到大多数的变量时近似服从正态分布的，但也有不服从正态分布的，不过我们先大致近似认为他们服从正态分布。

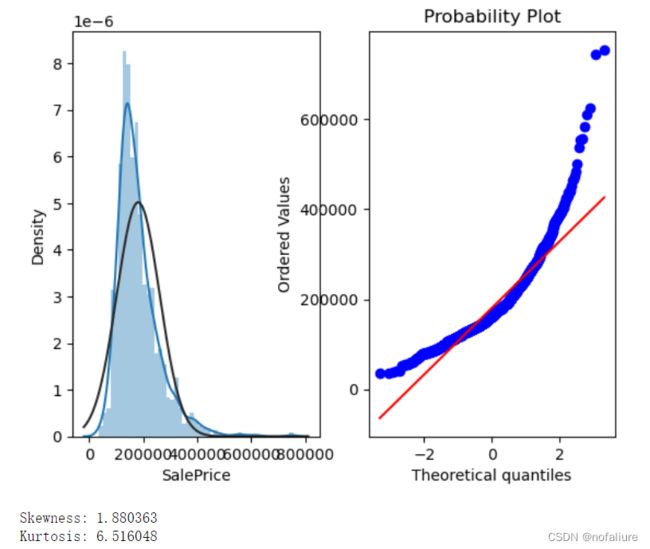
        对于价格，我们对其分析，看到价格存在正的尖峰值和倾斜度，可以通过取对数的方法使其服从正态分布。

plt.subplot(121)
sns.distplot(data['SalePrice'], fit=norm);
# qq图
# 有点像卡方分布
plt.subplot(122)
res = stats.probplot(data['SalePrice'], plot=plt)
plt.show()
print("Skewness: %f" % data['SalePrice'].skew())
print("Kurtosis: %f" % data['SalePrice'].kurt())

# 对数转换对于正偏态很有作用
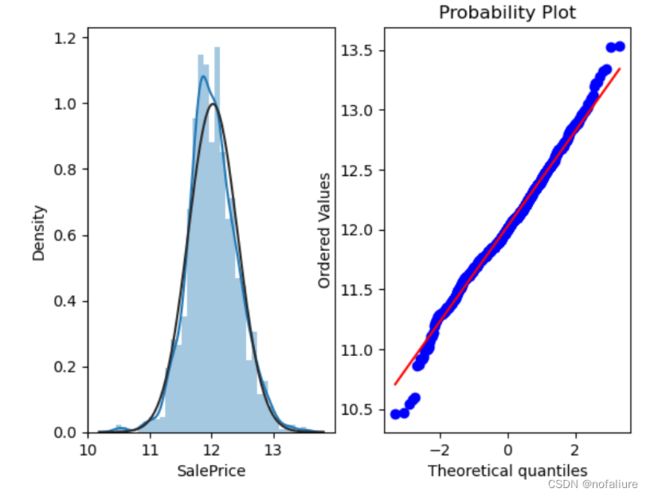
data_copy['SalePrice'] = np.log(data['SalePrice'])
# 再次作图
plt.subplot(121)
sns.distplot(data_copy['SalePrice'], fit=norm);
# qq图
plt.subplot(122)
res = stats.probplot(data_copy['SalePrice'], plot=plt)
plt.show()

        细心的同学可能看到了TotalBsmtS同样存在尖峰和倾斜度，是不是也可以通过这种方法去校正呢？但是大家要注意到这个变量是存在0值的，也就是说理论上对数是无穷大，在高等数学中是定义为不存在的，怎么分析呢？详见Comprehensive data exploration with Python | Kaggle

划分数据集和训练

        在划分数据集之前记得要对数据集进行标准化处理，以减小计算量，并且能够很大程度上减小不同量纲之间对于预测结果的影响。代码如下：

train_data=data_copy[main_factor]
# 数据集标准化
sc_x=StandardScaler()
sc_y=StandardScaler()
X=train_data[main_factor-set({'SalePrice'})]
y=train_data['SalePrice']
X,y=sc_x.fit_transform(X),sc_y.fit_transform(y.values.reshape((-1,1)))

# 20%作为测试集
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.2)

看一下各个预测器的得分

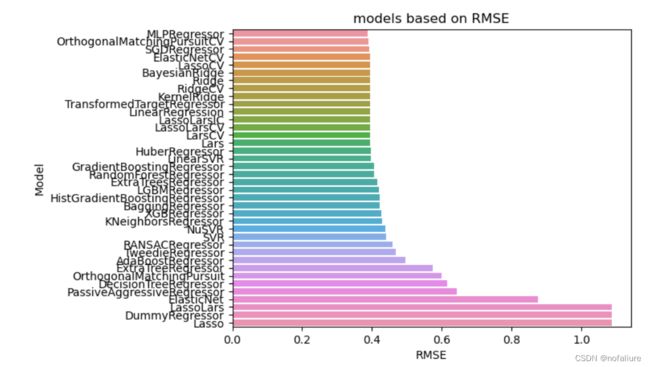
temp_df = model.sort_values('RMSE', ascending = True)[:-2]
sns.barplot(x = temp_df['RMSE'], y = temp_df.index).set_title('models based on RMSE')
plt.show()

         得分是根据均方误差来排名的，自然越小越好。之后就可以根据得分最高的回归器进行回归预测了。此外，我采用的是懒人预测办法，没有去调参，使用的都是默认参数，有兴趣的小伙伴可以自己去采用不同的模型去调节一下参数，看看哪个能得到最好的效果。 

The end