NLP(二)：n元模型
一. 语言建模(Language Modeling)
s1 = 我 刚 吃 过 早饭
s2 = 刚 我 过 早饭 吃
对于上面这两句话，很明显，s1读起来要比s2通顺的多，也就是说P(s1) > P(s2)；对于由n个词构成的不同句子(每个句子的基本组成词相同，只是顺序不同)，那么它们出现的概率是大大不同的，而这就引出了一个问题——对给定句子如何分配概率？我们需要建立一个模型来完成这件事！
对于给定的自然语言L，P(s)未知；利用给定的语言样本估计P(s)的过程被称作语言建模。
二. 语言模型(Language Model)
根据语料库中的样本估计出的概率分布P称为语言L的语言模型。通俗来讲语言模型就是用来计算句子概率的模型，那么如何对给定句子 s = w1w2…wl，如何计算P(s)？
可以应用链式规则，分解P(s):
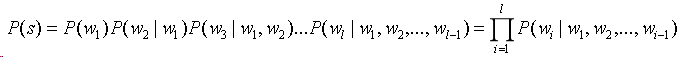其中P(w1)表示第一个出现的概率，P(w2|w1)表示已知第一个词w1的前提下第二词出现的概率，依此类推…，不难看出，词wl出现的概率取决于它前面所有词，这样的话，随着前面出现的词l的增长，参数的规模成指数增长，难以估算。
1. 马尔可夫假设
针对上面难以估算的问题，引入马尔可夫假设——任意一个词wi的出现只与其之前的n-1个词有关，即：
只需要考虑n个词组成的片段，即n元组(n-gram)
那么得到n元模型如下：
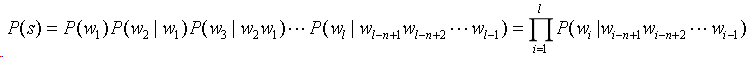
当n=1时，有一元模型(unigram):
当n=2时，有二元模型(bigram):
当n=3时，有三元模型(trigram):
（1）n元模型的参数
（2）n的选择
从（1）表中可以看出来，n越大，模型需要的参数越多，参数数量指数增长。而另一个方面，n越大，历史信息越多，模型就越准确。
A. n越大时
- 提供了更多的语境信息，语境更具有区别性；
- 参数个数多、计算代价大、训练语料需要多、参数估计不可靠；
B. n较小时
- 语境信息少，不具区别性；
- 但是，参数个数少、计算代价小、训练语料无需太多、参数估计可靠。
n元模型等价于n-1阶马尔可夫过程，即n元模型把句子看出是马尔可夫过程的产物；为此，为了 将出现在不同位置的同一个词区分开，并且保证n元模型对于句子中前n-1个词也有意义，我们需要加入标记bos来标志句子开始；为了保证词组合的句子出现的概率和为1，需要在句末加入eos来标志句子结束。
比如有一句话 s = “John read a book”，利用二元模型计算该句出现的概率：
2. 如何建立一个n元模型
数据准备：
- 确定训练语料库
- 对语料进行词例化或切分
- 句子边界标记，增加两个特殊的词和
参数估计：利用训练语料，估计模型参数。
（1）相对频率法
令c(w1,w2,…wn)表示n元组w1w2…wn在训练语料库中出现的次数，则：
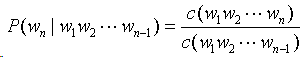
举个例子，我们有训练语料：
John read Moby Dick
Mary read a different book
She read a book by Cher
（2）最大似然估计
原则：选择使得训练样本似然值(概率)最大的参数
其中，theta 代表所有参数，即那些未知的条件的概率；P(T;theta)是训练语料的概率
我们在这里假设句子和句子之间是互相独立的，那么有：
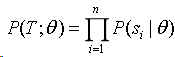
该优化问题具有解析解，让P(T;theta)达到最大的theta值可以用相对频率的估计值来近似，即
继续计算句子 John read a book 的概率：
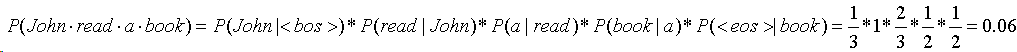由于语料库中的例很多，即使高频词组出现的频度也是很低的，而一个句子的频率是多个条件概率的乘积，这个值就更小了，而计算机表示浮点数时在某个位数之后就不准确了，这种现象称为计算下溢；因此为了避免这种情况发生，我们通常都是计算对数概率。
（3）数据稀疏(Data Sparseness)
考虑计算句子 Cher read a book 的概率，由于c(Cher read) = 0，会导致P(read | Cher) = 0，进而 P(Cher read a book) = 0，这显然是有问题的，我们知识换了个人名就导致这种现象概率为0，由此引出了一个问题——最大似然估计法(MLE)给训练样本中未观察到的事件赋0概率。这种由于训练样本不足而导致所估计的分布不可靠的问题称为数据稀疏问题。
如何解决上述问题呢？扩大训练语料的规模吗？有研究表明，语言中只有很少的常用词，大部分词都是低频词。将语料库的规模扩大，主要是高频词词例的增加，大多数词(n元组)在语料中的出现是稀疏的，因此扩大语料规模不能从根本上解决稀疏问题。
解决方法： 平滑(smoothing)
- 把在训练样本中出现过的事件的概率适当减小；
- 把减小得到的概率质量分配给训练语料中没有出现过的事件；
- 这个过程有时候也称为减值法(discounting)。
（4）Add-one 平滑
不同的减值策略导致不同的平滑方法，最简单的方法就是 Add-one 平滑。
Add-one 平滑：规定n元组比真实出现次数多一次，new_count(n-gram) = old_count(n-gram) + 1；没有出现过的n元组的概率不再是0，而是一个较小的概率值，实现了概率质量的重新分配。
先介绍一下词型(type)和词例(token)的区别："型"表示语料库中不同单词的数目，也就是词典容量的大小；"例"表示使用中的单词数目。
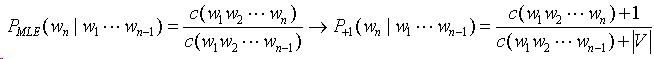
V代表词表，|V|代词表中词的数量。
A. 未使用平滑之前
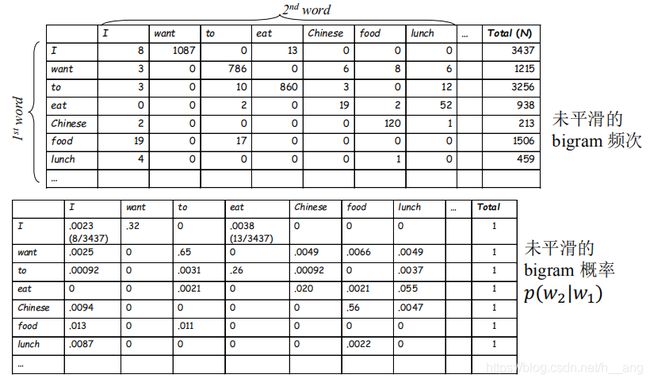上表是在Berkeley Restaurant Project语料库(容量约10000个句子)中，从1616个单词的"型"中选出7个单词进行二元计数；3437、1215、3256、938、213、1506、459分别表示I、want、to、eat、Chinese、food、lunch在语料库中出现的次数。
B. 使用平滑之后
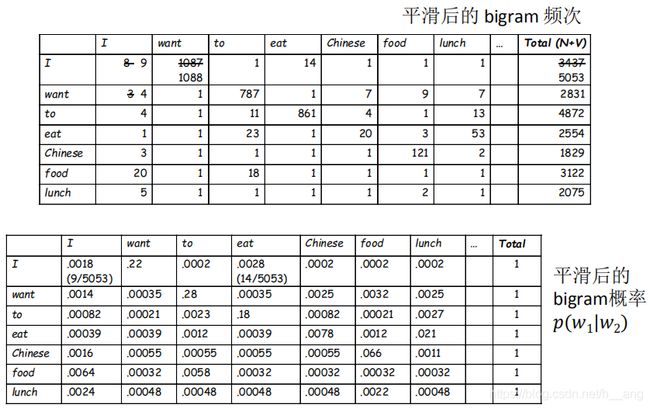
把 |V| = 1616分别加到每一个单元语法上面，分别得到5053、2831、4872、2554、1829、3122、2075。
Add-one 平滑的问题：由于训练语料中未出现n元组数量太多，平滑后，所有未出现的n元组占据了整个概率分布中的一个很大的比例。因此，在NLP中，Add-one给训练语料中没有出现过的n元组分配了太多的概率空间。并且给出现在训练预料中的那些n元组，都增加了同样的频度值，认为所有未出现的n元组概率相等，这是不合理的。
三. 语言模型的评价
1. 熵
（1）什么是熵？
设X是取有限个值的随机变量，若其概率分布为p(x)，且x属于X，则X的熵可以定义为：
通常a=2，此时熵的单位为bit（比特）；从确定性的角度来讲，熵表述了随机变量的不确定性；从信息量角度来讲，概率越小的事件蕴含越大的信息量，熵越大信息量越大，熵描述随机变量的平均信息量。
熵的基本性质 ：
A. H(X) >= 0，等号表示确定场（无随机性）的熵最小；
B. H(X) <= log |X|，等号表明等概场的熵最大。
（2）联合熵和条件熵
设X和Y是两个离散型随机变量，它们的联合分布为p(x,y)，则X、Y的联合熵定义为：
设X和Y是两个离散型随机变量，它们的联合分布为p(x,y)，则X、Y的条件熵定义为：
从信息量的角度考虑，联合熵H(X,Y)表示的是随机变量X和Y的信息量之和；条件熵H(Y|X)表示的是已知X的情况下Y的信息量；条件熵H(X|Y)表示的是已知Y的情况下X的信息量。
链式规则：H(X,Y) = H(X) + H(Y|X)
关于各种熵的实际意义以及它们之间的关系我之前的博客中有提及过：https://blog.csdn.net/h__ang/article/details/83870334
（3）相对熵
设p(x)是随机变量X的真实分布密度，q(x)是通过统计手段得到的X的近似分布，则二者之间的相对熵定义为：
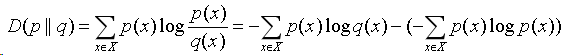
相对熵也称作KL发散度、KL距离，它提供了一种度量同一个随机变量在不同分布下差异的方法。从信息论的角度看，如果一个随机变量X的分布密度是p(x)，而人们却错误的使用了分布密度q(x)，相对熵描述了因为错用分布密度而增加的信息量。
（4）交叉熵
设p(x)是随机变量X的真实分布密度，q(x)是通过统计手段得到的X的近似分布，则二者之间的交叉熵定义为：
与相对熵的关系为： D(p || q) = H(X, q) - H(X)；
若存在X的两个近似分布q1(x)、q2(x)，H(X,q1) < H(X, q2)，则q1是更好的分布。
2. 语言模型的评价——交叉熵
令T为测试语料,有：
w在T中的经验分布为：
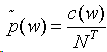
交叉熵衡量一元模型与测试语料经验分布之间的差异：
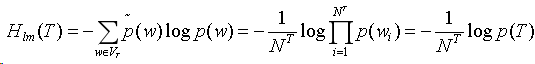
w1w2…wn在T中的经验分布为：
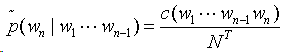
交叉熵衡量n元模型与测试语料经验分布的差异：
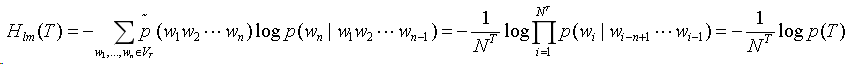由于交叉熵算出来的评价指标值比较小，因此语言模型的评价也可以使用困惑度：
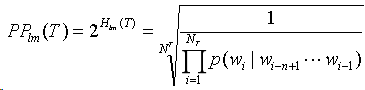
困惑度这个指标表示的是根据n元模型，正确采样wi的平均采样次数。