计算机视觉：朗伯光度立体法（Lambertian Photometric Stereo）

光度立体法简介

光度立体法，即Photometric Stereo, 最早是由当时在MIT的人工智能实验室的Robert J. Woodham教授在1978年左右提出。他在1979年的论文《Photometric stereo: A reflectance map technique for determining surface orientation from image intensity》，以及1980年的论文《Photometric Method for Determining Surface Orientation from Multiple Images》中比较系统的阐述了整套理论框架。光度立体法可以根据二维纹理信息提取出三维模型，其典型应用是检测物体表面微小变化。

朗伯光度立体法基于Woodham算法，Woodham在论文中提出三个基本假设。在这三个基本假设下完成整套理论框架的推演。这三个基本假设分别是：

1. 假定相机是无畸变成像，也就是说必须使用远心镜头或者长焦镜头。
2. 假定每一个光源发射的光束都是平行且均匀的，也就是说必须使用具有均匀强度的远心照明光源，或者使用远距离的点光源代替。
3. 物体必须具有朗伯（lambertian）反射特性，即它必须以漫反射的方式反射入射光。

朗伯光度立体法的大致思路是：
当相机和目标物体相对位置固定不变时，使用不同方向的光源照射同一目标物体，相机可以拍摄到目标物体带有不同明暗分布的图像（至少需要三张图），再通过求解基于朗伯反射原理的反射方程组，求解目标表面的法向分布或者albedo图。

带有远心镜头的相机必须与被测物体表面垂直安装，在采集多幅图像时，一定要保证相机和物体不被移动。相反，对于采集至少三张的灰度图像，其每次取像的照明方向必须改变（相对于相机）。对于采集的多张图像中的每一幅图，照明方向必须指定Slants和Tilts两个参数角度，其描述了相对于当前场景的光照角度。为了更好的理解这两个参数含义，我们假定光源射出的光束是平行光，镜头是远心镜头，相机垂直于物体表面。

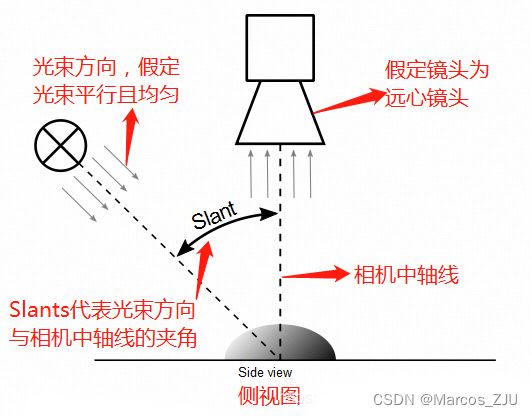
朗伯光度立体法算法原理

根据Lambert模型：
$$\text{I}=\rho \text{L}\cdot \text{N}$$
式中，$\rho$ 为表面反射率（albedo），其值介于0 - 1之间，反映了物体表面特性；$\text{N}$ 为表面法线（normal）；$\text{L}$ 为照明方向。将 $\rho$ 和 $\text{N}$ 合并起来用$\text{G}$来表示，则有：
$$\text{I}={\text{L}}^T\text{G}.$$
每个像素位置对应的$\text{G}$是三维向量（方向为normal，模长为albedo），因此单个光源无法求解该方程，至少需要三个不同位置的光源，求解得到三个未知量。
由最小二乘法：
$$\underset{\text{G}}{\min }||\text{I}-{\text{L}}^T\text{G}|{|}^2$$
可以求得：
$$\text{G}=(\text{L}{\text{L}}^T{)}^{-1}\text{L}\text{I}$$
我们求得 $\text{G}$ 的模长就是albedo:
$$\rho =||\text{G}||$$
$\text{G}$ 归一化后的单位向量矩阵就是normal:
$$\text{N}=\frac{\text{G}}{||\text{G}||}$$

朗伯光度立体法matlab程序

注：此代码只涉及核心算法，不包含数据的读入，与结果的输出。

function [Albedo, Normal, Re_rendered] = Photometric_Stereo(data)

assert(size(data.imgs, 1)==size(data.s, 1), 'Size mismatched!');
num = size(data.imgs, 1);

% Get image dimensions
im = data.imgs{1};
[im_h, im_w, ~] = size(im);
% Initialize T, a im_h-by-im_w-by-num matrix, whose (h, w, :) holds 
% the intensities at (h, w) for all p different lightings
im_T = zeros(im_h, im_w, num);
% Initialize im_R, a im_h-by-im_w-by-num matrix
im_R = zeros(im_h, im_w, num);
% Initialize im_G, a im_h-by-im_w-by-num matrix
im_G = zeros(im_h, im_w, num);
% Initialize im_B, a im_h-by-im_w-by-num matrix
im_B = zeros(im_h, im_w, num);

% For each image
for idx = 1:num
    im = data.imgs{idx};
    imGray = rgb2gray(im);
    % Loop thru each pixel
    for h = 1:im_h
        for w = 1:im_w
            % If in the mask
            if data.mask(h, w)
                im_R(h, w, idx) = im(h, w, 1);
                im_G(h, w, idx) = im(h, w, 2);
                im_B(h, w, idx) = im(h, w, 3);
                im_T(h, w, idx) = imGray(h,w);
            end
        end
    end
end

% Initialize Normal, a im_h-by-im_w-by-3 matrix
Normal = zeros(im_h, im_w, 3);
% Initialize Albedo, a im_h-by-im_w-by-1 matrix
Albedo = zeros(im_h, im_w, 3);
% Initialize Re_rendered, a im_h-by-im_w-by-3 matrix
Re_rendered = zeros(im_h, im_w, 3);

% Loop thru each location
for h = 1:im_h
    for w = 1:im_w
        % If in the mask
        if data.mask(h, w)
           %% Normal 
            % Lightings
            L = data.s;
            % Intensities
            I = reshape(im_T(h, w, :), [num, 1]);
            % Dealing with shadows and highlights
            for k = 1:10
                max_index = find(I==max(I));
                I(max_index) = [];
                L(max_index,:) = [];
                min_index = find(I==min(I));
                I(min_index) = [];
                L(min_index,:) = [];
            end
            % Solve surface normals and albedo
            G = (L.'*L)\(L.'*I);
            if norm(G) ~= 0
                % Normalize n
                n = G./norm(G);
            else
                n = [0; 0; 0];
            end
            % Save
            Normal(h, w, :) = n;
           %% Albedo
            % a_R
            L = data.s;
            I_R = reshape(im_R(h, w, :), [num, 1]);
            for k = 1:10
                max_index = find(I_R==max(I_R));
                I_R(max_index) = [];
                L(max_index,:) = [];
                min_index = find(I_R==min(I_R));
                I_R(min_index) = [];
                L(min_index,:) = [];
            end
            G_R = (L.'*L)\(L.'*I_R);
            a_R = norm(G_R);
            Albedo(h, w, 1) = a_R;
            % a_G
            L = data.s;
            I_G = reshape(im_G(h, w, :), [num, 1]);
            for k = 1:10
                max_index = find(I_G==max(I_G));
                I_G(max_index) = [];
                L(max_index,:) = [];
                min_index = find(I_G==min(I_G));
                I_G(min_index) = [];
                L(min_index,:) = [];
            end
            G_G = (L.'*L)\(L.'*I_G);
            a_G = norm(G_G);
            Albedo(h, w, 2) = a_G;
            % a_B
            L = data.s;
            I_B = reshape(im_B(h, w, :), [num, 1]);
            for k = 1:10
                max_index = find(I_B==max(I_B));
                I_B(max_index) = [];
                L(max_index,:) = [];
                min_index = find(I_B==min(I_B));
                I_B(min_index) = [];
                L(min_index,:) = [];
            end
            G_B = (L.'*L)\(L.'*I_B);
            a_B = norm(G_B);
            Albedo(h, w, 3) = a_B;
            %% Re_rendered
            Re_rendered(h, w, :) = [a_R;a_G;a_B]*dot(n,[0;0;1]);
        end
    end
end

示例

Albedo图

反照率图：

Normal图

以RGB线性编码的法线贴图：

Re_rendered图

在照明方向和观察方向一致时，利用normal和albedo图重新渲染的图片：

参考文献

光度立体简介
Halcon 光度立体法（photometric_stereo）详解z