Deep Convolutional Networks on Graph-Structured Data 汉译与理解

Deep Convolutional Networks on Graph-Structured Data 汉译与理解

Abstract

Deep Learning’s recent successes have mostly relied on Convolutional Networks, which exploit fundamental statistical properties of images, sounds and video data: the local stationarity and multi-scale compositional structure, that allows expressing long range interactions in terms of shorter, localized interactions. However, there exist other important examples, such as text documents or bioinformatic data, that may lack some or all of these strong statistical regularities. In this paper we consider the general question of how to construct deep architectures with small learning complexity on general non-Euclidean domains, which are typically unknown and need to be estimated from the data. In particular, we develop an extension of Spectral Networks which incorporates a Graph Estimation procedure, that we test on large-scale classification problems, matching or improving over Dropout Networks with far less parameters to estimate.

深度学习最近的成功主要依赖于卷积网络，它开发基础数据统计特性图像、声音和视频数据：局部平稳性和多尺度合成结构，允许用较短的局部交互来表达远程交互。然而，还有其他一些重要的例子，如文本文档或生物信息学数据，可能缺乏部分或全部这些强大的统计规律性。

**在本文中，我们考虑如何在一般的非欧几里德域上构造具有较小学习复杂度的深层体系结构，这些领域通常是未知的，需要从数据中进行估计。**特别是，我们开发了一个光谱网络的扩展，它包含了一个图估计程序，我们在大规模分类问题上进行测试，匹配或改进要估计的参数少得多的over-Dropout网络。

1 Introduction

In recent times,Deep Learning models have proven extremely successful on a wide variety of tasks, from computer vision and acoustic modeling to natural language processing[9]. At the core of their success lies an important assumption on the statistical properties of the data,namely the stationarity and the compositionality through local statistics, which are present in natural images, video, and speech. These properties are exploited efficiently by ConvNets [8,7],which are designed to extract local features that are shared across the signal domain. Thanks to this, they are able to greatly reduce the number of parameters in the network with respect to generic deep architectures, without sacrificing the capacity to extract informative statistics from the data. Similarly, Recurrent Neural Nets (RNNs) trained on temporal data implicitly assume a stationary distribution.

近年来，深度学习模型已经被证明在许多任务上都是非常成功的，从计算机视觉和声学建模到自然语言处理[9]。**其成功的核心在于对数据的统计特性的一个重要假设，即通过局部统计实现的平稳性和合成性，这些特性存在于自然图像、视频和语音中。**ConvNets[8,7]有效地利用了这些特性，**这些特性旨在提取信号域中共享的局部特征。由于这一点，它们能够在不损害从数据中提取信息统计信息的能力的情况下，相对于一般的深层架构，它们能够大大减少网络中的参数数量。**类似地，基于时间数据训练的递归神经网络（RNN）隐含地假设一个平稳分布。

One can think of such data examples as being signals defined on a low-dimensional grid. In this case stationarity is well defined via the natural translation operator on the grid, locality is defined via the metric of the grid, and compositionality is obtained from down-sampling, or equivalently thanks to the multi-resolution property of the grid. However, there exist many examples of data that lack the underlying low-dimensional grid structure. For example, text documents represented as bags of words can be thought of as signals defined on a graph whose nodes are vocabulary terms and whose weights represent some similarity measure between terms,such as co-occurrence statistics. In medicine, a patient’s gene expression data can be viewed as a signal defined on the graph imposed by the regulatory network. In fact, computer vision and audio, which are the main focus of research efforts in deep learning, only represent a special case of data defined on an extremely simple low dimensional graph. Complex graphs arising in other domains might be of higher dimension, and the statistical properties of data defined on such graphs might not satisfy the stationarity, locality and compositionality assumptions previously described. For such type of data of dimension N, deep learning strategies are reduced to learning with fully-connected layers, which have O(N^2) parameters, and regularization is carried out via weight decay and dropout [17].

我们可以把这样的数据示例看作是在低维网格上定义的信号。在这种情况下，平稳性是通过网格上的自然平移算子来定义的，局部性是通过网格的度量来定义的，而组成性是通过下采样获得的，或者由于网格的多分辨率特性而等价地获得的。然而，存在许多缺乏底层低维网格结构的数据示例。例如，以单词包表示的文本文档可以看作是在图上定义的信号，其节点是词汇术语，其权重表示术语之间的某种相似性度量，例如共现统计。在医学上，患者的基因表达数据可以看作是由调控网络施加在图形上的信号。事实上，作为深度学习研究重点的计算机视觉和音频，只代表了一个非常简单的低维图形数据的特例。在其他领域中产生的复杂图可能具有更高的维数，并且在这些图上定义的数据的统计特性可能不满足前面描述的平稳性、局部性和组合性假设。对于这类维数为N的数据，深度学习策略被简化为具有O(N^2)参数的全连通层的学习，并通过权重衰减和丢失进行正则化[17]。

When the graph structure of the input is known,[2] introduced a model to generalize ConvNets using low learning complexity similar to that of a ConvNet, and which was demonstrated on simple low dimensional graphs. In this work, we are interested in generalizing ConvNets to high-dimensional, general datasets,and, most importantly, to the setting where the graph structure is not known a priori. In this context, learning the graph structure amounts to estimating the similarity matrix, which has complexity O(N^2). One may therefore wonder whether the graph estimation followed by graph convolutions offers advantages with respect to learning directly from the data with fully connected layers. We attempt to answer this question experimentally and to establish baselines for future work.

在已知输入的图结构的情况下，[2]引入了一个与ConvNet相似的低学习复杂度的模型来推广ConvNet，并在简单的低维图上进行了证明。在这项工作中，**我们感兴趣的是将ConvNet推广到高维的、一般的数据集，并且，最重要的是，将其推广到图结构未知的情况下。在这种情况下，学习图的结构相当于估计相似矩阵，其复杂度为O（N^2）。因此，人们可能想知道，在直接从具有完全连接层的数据学习方面，图估计之后的图卷积是否具有优势。**我们试图通过实验来回答这个问题，并为将来的工作建立基础。

We explore these approaches in two areas of application for which it has not been possible to apply convolutional networks before: text categorization and bioinformatics. Our results show that our method is capable of matching or outperforming large, fully-connected networks trained with dropout using fewer parameters. Our main contributions can be summarized as follows:

​ • We extend the ideas from [2] to large-scale classification problems, specifically ImageNet Object Recognition, text categorization and bioinformatics.

​ • We consider the most general setting where no prior information on the graph structure is available, and propose unsupervised and new supervised graph estimation strategies in combination with the supervised graph convolutions.

我们在两个以前不可能应用卷积网络的应用领域探索这些方法：文本分类和生物信息学。**我们的结果表明，我们的方法可以匹配或优于大的，通过dropout方法训练的全连接网络且我们的方法只使用了较少的参数。**我们的主要贡献可以总结如下：

​ •我们将[2]的思想扩展到大规模分类问题，特别是ImageNet对象识别、文本分类和生物信息学。

​ •我们考虑在没有关于图结构的先验信息的最一般的情况下，结合有监督图卷积，提出了无监督和新的有监督图估计策略。

The rest of the paper is structured as follows. Section 2 reviews similar works in the literature. Section 3 discusses generalizations of convolutions on graphs, and Section 4 addresses the question of graph estimation. Finally, Section 5 shows numerical experiments on large scale object recognition, text categorization and bioinformatics.

论文的其余部分结构如下。第2节回顾了文献中类似的作品。第3节讨论图上卷积的推广，第4节讨论图估计的问题。最后，第5节给出了大规模目标识别、文本分类和生物信息学的数值实验。

2 Related Work

There have been several works which have explored architectures using the so-called local receptive fields [6, 4, 14], mostly with applications to image recognition. In particular, [4] proposes a scheme to learn how to group together features based upon a measure of similarity that is obtained in an unsupervised fashion. However, it does not attempt to exploit any weight-sharing strategy.

已经有一些工作探索了使用所谓的局部接收域的体系结构[6,4,14]，主要应用于图像识别。特别是，[4]提出了一个方案，学习如何根据以无监督方式获得的相似性度量将特征组合在一起。然而，它并没有试图利用任何权重分担策略。

Recently, [2] proposed a generalization of convolutions to graphs via the Graph Laplacian. By identifying a linear,translation-invariant operator in the grid (the Laplacian operator), with its counterpart in a general graph (the Graph Laplacian), one can view convolutions as the family of linear transforms commuting with the Laplacian. By combining this commutation property with a rule to find localized filters, the model requires only O(1) parameters per “feature map”. However, this construction requires prior knowledge of the graph structure, and was shown only on simple, low-dimensional graphs. More recently, [12] introduced ShapeNet, another generalization of convolutions on non-Euclidean domains based on geodesic polar coordinates, which was successfully applied to shape analysis, and allows comparison across different manifolds. However, it also requires prior knowledge of the manifolds.

最近，[2]提出了一种通过图拉普拉斯将卷积推广到图的方法。通过在网格中识别一个线性的、平移不变的算子（拉普拉斯算子）和它在一般图中的对应算子（拉普拉斯算子），**我们可以把卷积看作是与拉普拉斯算子交换的线性变换族。**通过将这种交换特性与查找局部滤波器的规则相结合，该模型只需要每个“特征映射”O（1）个参数。然而，这种构造需要对图结构的先验知识，并且只在简单的低维图上显示。最近，[12]引入了ShapeNet，这是基于测地极坐标的非欧几里德域卷积的另一种推广，它被成功地应用于形状分析，并允许在不同流形之间进行比较。然而，它也需要事先知道流形。

The graph or similarity estimation aspects have also been extensively studied in the past. For instance, [15] studies the estimation of the graph from a statistical point of view, through the identification of a certain graphical model using L1-penalized logistic regression. Also, [3] considers the problem of learning a deep architecture through a series of Haar contractions, which are learned using an unsupervised pairing criteria over the features.

在过去，图或相似性估计方面也得到了广泛的研究。例如，[15]**通过使用L1惩罚logistic回归识别某个图形模型，从统计学的角度研究图形的估计。**另外，[3]还考虑了通过一系列Haar收缩来学习深层架构的问题，这些收缩是通过使用特征上的无监督配对准则来学习的。

3 Generalizing Convolutions to Graphs

3.1 Spectral Networks

Our work builds upon [2] which introduced spectral networks. We recall the definition here and its main properties. A spectral network generalizes a convolutional network through the Graph Fourier Transform, which is in turn defined via a generalization of the Laplacian operator on the grid to the graph Laplacian. An input vector x ∈R^N is seen as a a signal defined on a graph G with N nodes.

我们的工作建立在[2]引入光谱网络的基础上。我们记得这里的定义及其主要特性。谱网络通过图Fourier变换将卷积网络泛化，然后通过将网格上的拉普拉斯算子推广到图Laplacian来定义卷积网络。一个输入向量x∈R^N被看作是一个在有N个节点的图G上定义的a信号。

Definition 1. Let W be a N × N similarity matrix representing an undirected graph G, and let
$$L=I-D^{-1/2}W{D}^{-1/2}$$
be its graph Laplacian with D = W ·1 eigenvectors U = (u_1,…,u_N). Then a graph convolution of input signals x with filters g on G is defined by
$$x{\ast }_{G}g=U^T(U_x\odot U_g),$$
where ⊙ represents a point-wise product.

定义1: 设W是表示无向图G的N×N相似矩阵，且令
$$L=I-D^{-1/2}W{D}^{-1/2}$$
为W的拉普拉斯图，D= W·1 特征向量U = (u_1,…,u_N)。然后输入信号x与滤波器g对g的卷积图定义为
$$x{\ast }_{G}g=U^T(U_x\odot U_g),$$
其中⊙表示点乘

Here, the unitary matrix U plays the role of the Fourier Transform in R^d. There are several ways of computing the graph Laplacian L [1]. In this paper, we choose the normalized version
$$L=I-D^{-1/2}W{D}^{-1/2}$$
,where D is a diagonal matrix with entries
$$D_{ii}={\Sigma }_j{W}_{ij}$$
. Note that in the case where W represents the lattice, from the definition of L we recover the discrete Laplacian operator ∆. Also note that the Laplacian commutes with the translation operator, which is diagonalized in the Fourier basis. It follows that the eigenvectors of ∆ are given by the Discrete Fourier Transform (DFT) matrix. We then recover a classical convolution operator by noting that convolutions are by definition linear operators that diagonalize in the Fourier domain (also known as the Convolution Theorem [11]).

在这里，酉矩阵U在R^d中起到Fourier变换的作用，有几种计算图Laplacian L的方法[1]。在本文中，我们选择了规范化版本:
$$L=I-D^{-1/2}W{D}^{-1/2}$$
其中，D是一个对角矩阵:
$$D_{ii}={\Sigma }_j{W}_{ij}$$
注意，在W代表格点的情况下，我们从L的定义中恢复离散拉普拉斯算子∆。还要注意的是，拉普拉斯算子与平移算符相乘，后者在傅立叶基中对角化。因此，∆的特征向量由离散傅立叶变换（DFT）矩阵给出。然后，我们通过定义在Fourier域中对角化的线性算子（也称为卷积定理[11]），恢复经典卷积算子。

Learning filters on a graph thus amounts to learning spectral multipliers w_g = (w_1,…,w_N)
$$x{\ast }_{G}g:=U^T(diag(w_g)Ux).$$
Extending the convolution to inputs x with multiple input channels is straightforward. If x is a signal with M input channels and N locations, we apply the transformation U on each channel, and then use multipliers
$$w_g=(w_{i,j};i\le N,j\le M).$$
However,for each feature map g we need convolutional kernels are typically restricted to have small spatial support, independent of the number of input pixels N, which enables the model to learn a number of parameters independent of N. In order to recover a similar learning complexity in the spectral domain,it is thus necessary to restrict the class of spectral multipliers to those corresponding to localized filters.

因此，在图上学习滤波器等于学习谱乘子w_g=（w_1，…，w N）
$$x{\ast }_{G}g:=U^T(diag(w_g)Ux).$$
将卷积扩展到具有多个输入通道的输入x非常简单。如果x是一个有M个输入通道和N个位置的信号，我们在每个通道上应用变换U，然后使用乘法器
$$w_g=(w_{i,j};i\le N,j\le M).$$
然而，对于每个特征映射g，我们需要卷积核具有较小的空间支持，与输入像素数N无关，这使得模型能够学习与N无关的多个参数。为了恢复谱域中类似的学习复杂度，因此，有必要将光谱倍增器的类别限制为与局部滤波器相对应的类别。

For that purpose, we seek to express spatial localization of filters in terms of their spectral multipliers. In the grid, smoothness in the frequency domain corresponds to the spatial decay, since
$$|\frac{{\partial }^k\hat{x}(\xi )}{\partial {\xi }^k}|\le C\int |u{|}^k|x(u)|du$$
where ˆ x(ξ) is the Fourier transform of x. In [2] it was suggested to use the same principle in a general graph, by considering a smoothing kernel K ∈ R^(N×N_0), such as splines, and searching for spectral multipliers of the form
$$w_g=K{\tilde{w}}_g$$
The algorithm which implements the graph convolution is described in Algorithm 1.

为此，我们寻求用光谱倍增器来表达滤波器的空间局部化。在网格中，频域中的平滑度对应于空间衰减，因为
$$|\frac{{\partial }^k\hat{x}(\xi )}{\partial {\xi }^k}|\le C\int |u{|}^k|x(u)|du$$
式中，ˆx(ξ)是x的Fourier变换，在[2]中建议在一般图中使用相同的原理，通过考虑光滑核K∈R^(N×N_0)，如样条，并搜索形式的谱乘子
$$w_g=K{\tilde{w}}_g$$
算法1描述了实现图卷积的算法。

3.2 Pooling with Hierarchical Graph Clustering

In image and speech applications, and in order to reduce the complexity of the model, it is often useful to trade off spatial resolution for feature resolution as the representation becomes deeper. For that purpose, pooling layers compute statistics in local neighborhoods, such as the average amplitude, energy or maximum activation.

The same layers can be defined in a graph by providing the equivalent notion of neighborhood. In this work, we construct such neighborhoods at different scales using multi-resolution spectral clustering [20], and consider both average and max-pooling as in standard convolutional network architectures.

在图像和语音应用中，为了降低模型的复杂度，随着表示的加深，在空间分辨率和特征分辨率之间进行权衡是非常有用的。为此，汇聚层计算局部邻域的统计信息，例如平均振幅、能量或最大激活。

通过提供等效的邻域概念，可以在图中定义相同的层。在这项工作中，我们使用多分辨率谱聚类[20]在不同的尺度上构造这样的邻域，并考虑在标准卷积网络体系结构中的平均和最大池。

4 Graph Construction

Whereas some recognition tasks in non-Euclidean domains, such as those considered in [2] or [12], might have a prior knowledge of the graph structure of the input data, many other real-world applications do not have such knowledge. It is thus necessary to estimate a similarity matrix W from the data before constructing the spectral network. In this paper we consider two possible graph constructions, one unsupervised by measuring joint feature statistics, and another one supervised using an initial network as a proxy for the estimation.

虽然非欧几里德域中的一些识别任务，如[2]或[12]中考虑的任务，可能事先知道输入数据的图形结构，但许多其他实际应用程序不具备这种知识。因此，在构造光谱网络之前，需要从数据中估计相似矩阵W。在本文中，我们考虑两种可能的图构造，一种是通过测量联合特征统计量进行监督的，另一种是使用初始网络作为估计的代理来监督的。

4.1 Unsupervised Graph Estimation

Given data X ∈ R^L×N, where L is the number of samples and N the number of features, the simplest approach to estimating a graph structure from the data is to consider a distance between features i and j given by
$$d(i,j)=||X_i-X_j|{|}^2$$
, where X_i is the i-th column of X. While correlations are typically sufficient to reveal the intrinsic geometrical structure of images[16], the effects of higher-order statistics might be non-negligible in other contexts, especially in presence of sparsity. Indeed, in many situations the pairwise Euclidean distances might suffer from unnormalized measurements. Several strategies and variants exist to gain some robustness, for instance replacing the Euclidean distance by the Z-score (thus renormalizing each feature by its standard deviation), the “square-correlation” (computing the correlation of squares of previously whitened features), or the mutual information.

给定数据X∈R^L×N，其中L是样本数，N是特征数，根据数据估计图结构的最简单方法是考虑下式给出的特征i和j之间的距离
$$d(i,j)=||X_i-X_j|{|}^2$$
其中X_i是X的第i列。虽然相关性通常足以揭示图像的内在几何结构[16]，但在其他情况下，高阶统计的影响可能是不可忽略的，尤其是在稀疏的情况下。实际上，在许多情况下，成对欧几里德距离可能会受到非规范化测量的影响。存在几种策略和变体来获得一些鲁棒性，例如用Z分数代替欧几里德距离（从而通过其标准差重新规范化每个特征）、“平方相关”（计算先前白化特征的平方相关性）或互信息。

This distance is then used to build a Gaussian diffusion Kernel [1]
$$w(i,j)=ex{p}^{-\frac{d(i,j)}{{\sigma }^2}}(1)$$
In our experiments, we also consider the variant of self-tuning diffusion kernel [21]
$$w(i,j)=ex{p}^{-\frac{d(i,j)}{{\sigma }_i{\sigma }_j}}$$
where σ_i is computed as the distance d(i,i_k) corresponding to the k-th nearest neighbor i_k of feature i. This defines a kernel whose variance is locally adapted around each feature point, as opposed to (1) where the variance is shared.

然后用这个距离建立高斯扩散核[1]
$$w(i,j)=ex{p}^{-\frac{d(i,j)}{{\sigma }^2}}(1)$$
在我们的实验中，我们还考虑了自校正扩散核的变体[21]
$$w(i,j)=ex{p}^{-\frac{d(i,j)}{{\sigma }_i{\sigma }_j}}$$
式中，σ_i计算为与特征i的第k个最近邻iаk相对应的距离d（i，i_k）。这定义了一个核，其方差在每个特征点附近局部调整，而不是（1）在这里方差是共享的。

4.2 Supervised Graph Estimation

As discussed in the previous section, the notion of feature similarity is not well defined, as it depends on our choice of kernel and criteria. Therefore, in the context of supervised learning, the relevant statistics from the input signals might not correspond to our imposed similarity criteria. It may thus be interesting to ask for the feature similarity that best suits a particular classification task.

如前一节所讨论的，特征相似性的概念并没有很好地定义，因为它取决于我们对内核和标准的选择。因此，在有监督学习的背景下，来自输入信号的相关统计信息可能不符合我们设定的相似性准则。因此，询问最适合特定分类任务的特征相似性可能很有趣。

A particularly simple approach is to use a fully-connected network to determine the feature similarity. Given a training set with normalized 1 features X ∈ R^L×N and labels y ∈ {1,…,C}L, we initially train a fully connected network φ with K layers of weights W_1,…,W_K, using standard ReLU activations and dropout. We then extract the first layer features W_1 ∈ R^N×M_1, where M_1 is the number of first-layer hidden features, and consider the distance
$$d_{sup}(i,j)=||W_{1,i}-W_{1,j}|{|}^2,(2)$$
that is then fed into the Gaussian kernel as in (1). The interpretation is that the supervised criterion will extract through W_1 a collection of linear measurements that best serve the classification task. Thus two features are similar if the network decides to use them similarly within these linear measurements.

一种特别简单的方法是使用完全连通的网络来确定特征相似性。给定一个标准化1特征X∈R^{L×N和标签y∈{1,…，C}L的训练集，利用标准的ReLU激活和丢失训练一个具有K层权值的全连通网络φ。然后提取第一层特征W_1∈R}N×M_1，其中M_1是第一层隐藏特征的数量，并考虑距离
$$d_{sup}(i,j)=||W_{1,i}-W_{1,j}|{|}^2,(2)$$
然后输入高斯核，如（1）所示。解释是，监督标准将通过W_1提取最适合分类任务的线性测量集合。因此，如果网络决定在这些线性测量中相似地使用它们，那么这两个特征是相似的。

This constructions can be seen as “distilling” the information learned by a first network into a kernel. In the general case where no assumptions are made on the dimension of the graph, it amounts to extracting N^2/2 parameters from the first learning stage (which typically involves a much larger number of parameters). If, moreover, we assume a low-dimensional graph structure of dimension m,then mN parameters are extracted by projecting the resulting kernel into its leading m directions.

这种构造可以看作是将第一个网络学习到的信息“提取”到内核中。在一般情况下，没有假设图的维数，这相当于从第一个学习阶段提取N^2/2个参数（这通常涉及更多的参数）。此外，如果我们假设一个低维的m维图结构，则通过将得到的核投影到其前导m方向来提取mN参数。

Finally, observe that one could simply replace the eigen-basis U obtained by diagonalizing the graph Laplacian by an arbitrary unitary matrix, which is then optimized by back-propagation together with the rest of the parameters of the model. We do not report results on this strategy, although we point out that it has the same learning complexity as the Fully Connected network (requiring O(KN^2) parameters, where K is the number of layers and N is the input dimension).

最后，观察到我们可以简单地用任意酉矩阵代替拉普拉斯图对角化得到的特征基U，然后通过反向传播和模型的其他参数一起优化。虽然我们指出该策略与全连通网络具有相同的学习复杂度（需要O（KN^2）参数，其中K是层数，N是输入维），但是我们没有报告这种策略的结果。

5 Experiments

In order to measure the performance of spectral networks on real-world data and to explore the effect of the graph estimation procedure, we conducted experiments on three datasets from text categorization, computational biology and computer vision. All experiments were done using the Torch machine learning environment with a custom CUDA backend.

为了测量光谱网络对真实世界数据的性能，并探讨图估计过程的效果，我们在文本分类、计算生物学和计算机视觉三个数据集上进行了实验。所有的实验都是用一个定制的CUDA 后端的Torch学习环境完成的。

We based the spectral network architecture on that of a classical convolutional network, namely by interleaving graph convolution, ReLU and graph pooling layers, and ending with one or more fully connected layers. As noted above, training a spectral network requires an O(N^2) matrix multiplication for each input and output feature map to perform the Graph Fourier Transform, compared to the efficient O(NlogN) Fast Fourier Transform used in classical ConvNets. We found that training the spectral networks with large numbers of feature maps to be very time-consuming and therefore chose to experiment mostly with architectures with fewer feature maps and smaller pool sizes. We found that performing pooling at the beginning of the network was especially important to reduce the dimensionality in the graph domain and mitigate the cost of the expensive Graph Fourier Transform operation.

我们在经典卷积网络结构的基础上，通过交织图卷积、ReLU和图池层，并以一个或多个完全连接的层结束。如上所述，与经典ConvNets中使用的高效O(NlogN) 快速傅立叶变换相比，训练光谱网络需要对每个输入和输出特征映射进行O(N^2)矩阵乘法来执行图形傅立叶变换。我们发现用大量的特征映射来训练光谱网络是非常耗时的，因此选择使用较少的特征映射和较小的池大小来进行实验。我们发现，在网络开始时执行池对于降低图域的维数和降低昂贵的图傅立叶变换操作的成本特别重要。

In this section we adopt the following notation to describe network architectures: GCk denotes a graph convolution layer with k feature maps, Pk denotes a graph pooling layer with stride k and pool size 2k, and FCk denotes a fully connected layer with k hidden units. In our results we also denote the number of free parameters in the network by P_net and the number of free parameters when estimating the graph by P_graph.

在本节中，我们采用以下符号来描述网络结构：GCk表示具有k个特征映射的图卷积层，Pk表示具有步长k和池大小2k的图池层，FCk表示具有k个隐藏单元的完全连接层。在我们的结果中，我们还用P_net 表示网络中的自由参数个数，以及用P_graph 估计图时的自由参数个数。

5.1 Reuters

We used the Reuters dataset described in [18], which consists of training and test sets each containing 201,369 documents from 50 mutually exclusive classes. Each document is represented as a log-normalized bag of words for 2000 common non-stop words. As a baseline we used the fully connected network of [18] with two hidden layers consisting of 2000 and 1000 hidden units regularized with dropout.

我们使用了[18]中描述的路透社数据集，该数据集由训练集和测试集组成，每个集包含来自50个互斥类的201369个文档。每个文档都表示为一个日志规范化的单词包，其中包含2000个常用的不间断单词。作为基线，我们使用了[18]的全连通网络，其中两个隐藏层分别由2000和1000个隐藏单元组成，使用dropout来正则化。

We chose hyper-parameters by performing initial experiments on a validation set consisting of one tenth of the training data. Specifically,we set the number of sub-sampled weights to k = 60,learning rate to 0.01 and used max pooling rather than average pooling. We also found that using AdaGrad [5] made training faster. All architectures were then trained using the same hyper-parameters. Since the experiments were computationally expensive, we did not train all models until full convergence. This enabled us to explore more model architectures and obtain a clearer under standing of the effects of graph construction.

我们通过在包含十分之一训练数据的验证集上进行初始实验来选择超参数。具体来说，我们将子样本权重的数量设置为k=60，学习率设置为0.01，并使用最大池而不是平均池。我们还发现使用AdaGrad[5]可以加快训练速度。然后使用相同的超参数训练所有的体系结构。由于实验的计算成本很高，我们在完全收敛之前并没有训练所有的模型。这使我们能够探索更多的模型体系结构，并对图构造的效果有一个更清晰的认识。

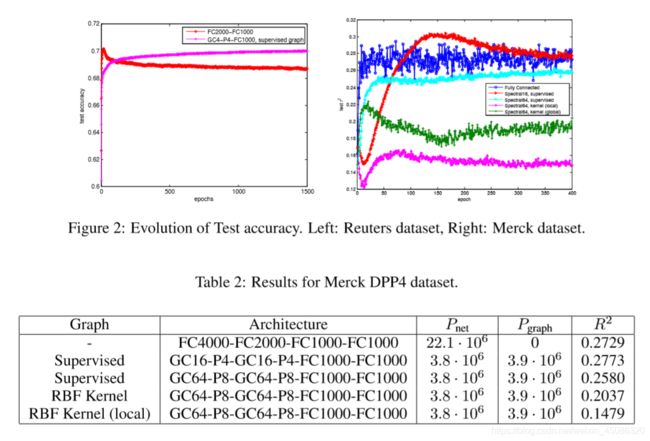
Note that our architectures are designed so that they factor the first hidden layer of the fully connected network across feature maps and a sub-sampled graph, trading off resolution in the graph domain for resolution across feature maps. The number of inputs into the last fully connected layer is always the same as for the fully-connected network. The idea is to reduce the number of parameters in the first layer of the network while avoiding too much compression in the second layer. We note that as we increase the tradeoff between resolution in the graph domain and across features, there reaches a point where performance begins to suffer. This is especially pronounced for the unsupervised graph estimation strategies. When using the supervised method, the network is much more robust to the factorization of the first layer. Table 1 compares the test accuracy of the fully connected network and the GC4-P4-FC1000 network. Figure 5.2-left shows that the factorization of the lower layer has a beneficial regularizing effect.

请注意，我们的体系结构是这样设计的，它们考虑了特征图和子采样图之间完全连接网络的第一个隐藏层，在图域中的分辨率与跨特征图的分辨率进行权衡。最后一个完全连接层的输入数量始终与完全连接的网络相同。这样做的目的是减少网络第一层的参数数量，同时避免第二层的过多压缩。我们注意到，当我们在图域中增加分辨率和跨特性之间的折衷时，性能就会开始受到影响。这对于无监督图估计策略尤为明显。当使用监督方法时，网络对第一层的因子分解更为稳健。表1比较了全连接网络和GC4-P4-FC1000网络的测试精度。图5.2-左图显示，下层的因子分解具有有益的正则化效果。

5.2 Merck Molecular Activity Challenge

The Merck Molecular Activity Challenge is a computational biology benchmark where the task is to predict activity levels for various molecules based on the distances in bonds between different atoms. For our experiments we used the DPP4 dataset which has 8193 samples and 2796 features. We chose this dataset because it was one of the more challenging and was of relatively low dimensionality which made the spectral networks tractable. As a baseline architecture,we used the network of [10] which has 4 hidden layers and is regularized using dropout and weight decay. We used the same hyper-parameter settings and data normalization recommended in the paper.

默克分子活性挑战赛是一个计算生物学基准，其任务是根据不同原子之间的键间距来预测各种分子的活性水平。在我们的实验中，我们使用了 DPP4 数据集，它有8193个样本和2796个特征。我们选择这个数据集是因为它是一个更具挑战性的数据集，并且具有相对较低的维数，这使得光谱网络易于处理。作为一个基线架构，我们使用了[10]的网络，它有4个隐藏层，并使用丢失和权重衰减进行正则化。我们使用了文中推荐的相同的超参数设置和数据规范化。

As before, we used one-tenth of the training set to tune hyper-parameters of the network. For this task we found that k = 40 sub-sampled weights worked best, and that average pooling performed better than max pooling. Since the task is to predict a continuous variable, all networks were trained by minimizing the Root Mean-Squared Error loss. Following [10], we measured performance by computing the squared correlation between predictions and targets.

和以前一样，我们使用十分之一的训练集来调整网络的超参数。对于这个任务，我们发现k=40的子抽样权重效果最好，平均池的性能比max池好。由于任务是预测一个连续变量，所有网络都是通过最小化均方根误差损失来训练的。在[10]之后，我们通过计算预测和目标之间的平方相关来衡量性能。

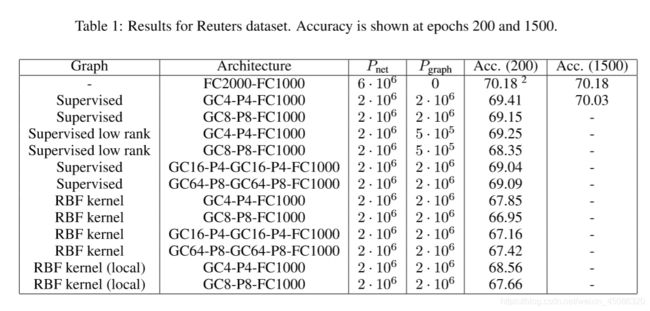
We again designed our architectures to factor the first two hidden layers of the fully-connected network across feature maps and a sub-sampled graph, and left the second two layers unchanged. As before, we see that the unsupervised graph estimation strategies yield a significant drop in performance whereas the supervised strategy enables our network to perform similarly to the fully-connected network with much fewer parameters. This indicates that it is able to factor the lower-level representations in such a way as to retain useful information for the classification task.

我们再次设计了我们的体系结构，将完全连接网络的前两个隐藏层与特征图和子采样图相结合，并保持后两个层不变。如前所述，我们看到，无监督图估计策略会显著降低性能，而有监督策略使我们的网络能够以更少的参数执行与完全连接的网络相似的性能。这表明它能够以这样一种方式考虑较低级别的表示，以便为分类任务保留有用的信息。

Figure 5.2-right shows the test performance as the models are being trained. We note that the Merck datasets have test set samples assayed at a different time than the samples in the training set, and thus the distribution of features is typically different between the training and test sets. Therefore the test performance can be a significantly noisy function of the train performance. However, the effect of the different graph estimation procedures is still clear.

图5.2-右图显示了模型接受培训时的测试性能。我们注意到，默克数据集的测试集样本在不同的时间进行分析，而训练集和测试集的特征分布通常不同。因此，试验性能可能是列车性能的显著噪声函数。然而，不同的图估计程序的效果仍然很明显。

5.3 ImageNet

In the experiments above our graph construction relied on estimation from the data. To measure the influence of the graph construction compared to the filter learning in the graph frequency domain, we performed the same experiments on the ImageNet dataset for which the graph is already known, namely it is the 2-D grid. The spectral network was thus a convolutional network whose weights were defined in the frequency domain using frequency smoothing rather than imposing compactly supported filters. Training was performed exactly as in Figure 1, except that the linear transformation was a Fast Fourier Transform.

在上面的实验中，我们的图的构造依赖于对数据的估计。为了测量图形构建与过滤学习在图形频域中的影响，我们对已知图形的ImageNet数据集（即二维网格）进行了相同的实验。因此，光谱网络是一个卷积网络，其权重在频域中使用频率平滑而不是施加紧支撑滤波器来确定。训练完全如图1所示，只是线性变换是快速傅立叶变换。

Our network consisted of 4 convolution/ReLU/max pooling layers with 48,128,256 and 256 feature maps, followed by 3 fully-connected layers each with 4096 hidden units regularized with dropout. We trained two versions of the network: one classical convolutional network and one as a spectral network where the weights were defined in the frequency domain only and were interpolated using a spline kernel. Both networks were trained for 40 epochs over the ImageNet dataset where input images were scaled down to 128×128 to accelerate training.

我们的网络由4个卷积/ReLU/max池层组成，其中有48128256和256个特征图，然后是3个完全连接的层，每个层有4096个隐藏单元，并通过丢失进行正则化。我们训练了两个版本的网络：一个是经典的卷积网络，另一个是谱网络，其中权值仅在频域中定义，并使用样条核插值。两个网络都在ImageNet数据集上训练了40个时期，输入图像被缩小到128×128以加速训练。

We see that both models yield nearly identical performance. Interestingly, the spectral network learns faster than the ConvNet during the first part of training, although both networks converge around the same time. This requires further investigation.

我们发现两种模型的性能几乎相同。有趣的是，在训练的第一部分，光谱网络的学习速度比ConvNet快，尽管两个网络在同一时间收敛。这需要进一步调查。

6 Discussion

ConvNet architectures base their appeal and success on their ability to produce highly informative local statistics using low learning complexity and avoiding expensive matrix multiplications. This motivated us to consider generalizations on high-dimensional, unstructured data.

**ConvNet体系结构的吸引力和成功的基础是能够使用低学习复杂度和避免昂贵的矩阵乘法来生成高信息量的本地统计数据。**这促使我们考虑对高维、非结构化数据进行泛化。

When the statistical properties of the input satisfy both stationarity and compositionality, spectral networks have a learning complexity of the same order as ConvNets. In the general setting where no prior knowledge of the input graph structure is known, our model requires estimating the similarities, a O(N^2) operation, but making the model deeper does not increase learning complexity as much as the general Fully Connected architectures. Moreover, in contexts where feature similarities can be estimated using unlabeled data (such as word representations), our model has less parameters to learn from labeled data.

However, as our results demonstrate, their extension poses significant challenges:

当输入的统计特性同时满足平稳性和组合性时，谱网络具有与ConvNets相同阶次的学习复杂度。在不知道输入图结构先验知识的一般情况下，我们的模型需要估计相似性，一个O(N^2)操作，但是使模型更深入并不像一般的全连接体系结构那样增加学习复杂度。此外，在可以使用未标记数据（如单词表示）来估计特征相似性的上下文中，我们的模型从标记数据中学习的参数较少。

然而，正如我们的结果所示，它们的扩展带来了巨大的挑战：

​ • Although the learning complexity requires O(1) parameters per feature map, the evaluation,both forward and backward, requires a multiplication by the Graph Fourier Transform, which costs O(N^2) operations. This is a major difference with respect to traditional ConvNets, which require only O(N). Fourier implementations of ConvNets [13, 19] bring the complexity to O(NlogN) thanks again to the specific symmetries of the grid. An open question is whether one can find approximate eigenbasis of general Graph Laplacians using Givens’ decompositions similar to those of the FFT.

​ •尽管学习复杂度要求每个特征图有O(1)个参数，但正向和反向评估都需要乘以图的傅里叶变换，这需要O(N^2)运算。这是与传统ConvNet的一个主要区别，后者只需要O(N)。ConvNets的Fourier实现[13，19]再次由于网格的特殊对称性，给O(NlogN)带来了复杂性。一个悬而未决的问题是，是否可以找到一般图拉普拉斯的近似特征基使用Givens的分解类似于那些FFT。

​ • Our experiments show that when the input graph structure is not known a priori, graph estimation is the statistical bottleneck of the model, requiring O(N^2) for general graphs and O(MN) for M-dimensional graphs. Supervised graph estimation performs significantly better than unsupervised graph estimation based on low-order moments. Furthermore, we have verified that the architecture is quite sensitive to graph estimation errors. In the supervised setting, this step can be viewed in terms of a Bootstrapping mechanism, where an initially unconstrained network is self-adjusted to become more localized and with weight sharing.

•我们的实验表明，当输入图结构未知时，图估计是模型的统计瓶颈，一般图需要O(N^2)，M维图需要O(MN)。有监督图估计的性能明显优于基于低阶矩的无监督图估计。此外，我们还验证了该体系结构对图估计误差非常敏感。在有监督的情况下，这一步可以用自举机制来看待，在这种机制中，一个初始的无约束网络会自我调整，使其变得更加局部化，并且具有权重共享。

• Finally, the statistical assumptions of stationarity and compositionality are not always verified. In those situations, the constraints imposed by the model risk to reduce its capacity for no reason. One possibility for addressing this issue is to insert Fully connected layers between the input and the spectral layers, such that data can be transformed into the appropriate statistical model. Another strategy, that is left for future work, is to relax the notion of weight sharing by introducing instead a commutation error
$$||W_{i}L-L{W}_i||$$
with the graph Laplacian, which puts a soft penalty on transformations that do not commute with the Laplacian, instead of imposing exact commutation as is the case in the spectral net.

•最后，平稳性和组成性的统计假设并不总是得到验证。在这些情况下，模型施加的约束有可能无缘无故地降低其容量。解决这个问题的一种可能性是在输入层和光谱层之间插入完全连接的层，这样数据就可以转换成适当的统计模型。另一个策略，留给未来的工作，是用拉普拉斯图通过引入一个交换误差来放松权重分担的概念:
$$||W_{i}L-L{W}_i||$$
对不与拉普拉斯变换的变换施加一个软惩罚，而不是像在谱网中那样施加精确的交换。

References

[1] Mikhail Belkin and Partha Niyogi. Laplacian eigenmaps and spectral techniques for embedding and clustering. In NIPS, volume 14, pages 585–591, 2001.

[2] Joan Bruna, Wojciech Zaremba, Arthur Szlam, and Yann LeCun. Spectral networks and deep locally connected networks on graphs. In Proceedings of the 2nd International Conference on Learning Representations, 2013.

[3] XuChen,XiuyuanCheng,andSt´ephaneMallat. Unsuperviseddeephaarscatteringongraphs. In Advances in Neural Information Processing Systems, pages 1709–1717, 2014.

[4] Adam Coates and Andrew Y Ng. Selecting receptive fields in deep networks. In Advances in Neural Information Processing Systems, pages 2528–2536, 2011.

[5] JohnDuchi,EladHazan,andYoramSinger. Adaptivesubgradientmethodsforonlinelearning andstochasticoptimization. TheJournalofMachineLearningResearch,12:2121–2159,2011.

[6] Karol Gregor and Yann LeCun. Emergence of complex-like cells in a temporal product network with local receptive fields. arXiv preprint arXiv:1006.0448, 2010.

[7] Geoffrey Hinton, Li Deng, Dong Yu, George Dahl, Abdel rahman Mohamed, Navdeep Jaitly, AndrewSenior,VincentVanhoucke,PatrickNguyen,TaraSainath,andBrianKingsbury. Deep neural networks for acoustic modeling in speech recognition. Signal Processing Magazine, 2012.

[8] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. Imagenet classification with deep convolutional neural networks. In F. Pereira, C.J.C. Burges, L. Bottou, and K.Q. Weinberger, editors, Advances in Neural Information Processing Systems 25, pages 1097–1105. Curran Associates, Inc., 2012.

[9] Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. Nature, 521(7553):436– 444, 05 2015.

[10] JunshuiMa,RobertP.Sheridan,AndyLiaw,GeorgeE.Dahl,andVladimirSvetnik. Deepneural networks as a method for quantitative structure-activity relationships. Journal of Chemical Information and Modeling, 2015.

[11] St´ephane Mallat. A wavelet tour of signal processing. Academic press, 1999.

[12] JonathanMasci,DavideBoscaini,MichaelM.Bronstein,andPierreVandergheynst. Shapenet: Convolutional neural networks on non-euclidean manifolds. CoRR, abs/1501.06297, 2015.

[13] Michael Mathieu, Mikael Henaff, and Yann LeCun. Fast training of convolutional networks through ffts. arXiv preprint arXiv:1312.5851, 2013.

[14] Jiquan Ngiam, Zhenghao Chen, Daniel Chia, Pang W Koh, Quoc V Le, and Andrew Y Ng. Tiled convolutional neural networks. In Advances in Neural Information Processing Systems, pages 1279–1287, 2010.

[15] Pradeep Ravikumar, Martin J Wainwright, John D Lafferty, et al. High-dimensional ising model selection using `1-regularized logistic regression. The Annals of Statistics, 38(3):1287– 1319, 2010.

[16] Nicolas L Roux, Yoshua Bengio, Pascal Lamblin, Marc Joliveau, and Bal´azs K´egl. Learning the 2-d topology of images. In Advances in Neural Information Processing Systems, pages 841–848, 2008.

[17] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1):1929–1958, 2014.

[18] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15:1929–1958, 2014.

[19] Nicolas Vasilache, Jeff Johnson, Micha¨el Mathieu, Soumith Chintala, Serkan Piantino, and Yann LeCun. Fast convolutional nets with fbfft: A GPU performance evaluation. CoRR, abs/1412.7580, 2014.

[20] Ulrike Von Luxburg. A tutorial on spectral clustering. Statistics and computing, 17(4):395– 416, 2007.

[21] Lihi Zelnik-Manor and Pietro Perona. Self-tuning spectral clustering. In Advances in neural information processing systems, pages 1601–1608, 2004.

athieu, Soumith Chintala, Serkan Piantino, and Yann LeCun. Fast convolutional nets with fbfft: A GPU performance evaluation. CoRR, abs/1412.7580, 2014.

[20] Ulrike Von Luxburg. A tutorial on spectral clustering. Statistics and computing, 17(4):395– 416, 2007.

[21] Lihi Zelnik-Manor and Pietro Perona. Self-tuning spectral clustering. In Advances in neural information processing systems, pages 1601–1608, 2004.

施工中……有错请指出