【点云系列】Unsupervised Multi-Task Feature Learning on Point Clouds
1. 概要
题目:Unsupervised Multi-Task Feature Learning on Point Clouds
论文:https://openaccess.thecvf.com/content_ICCV_2019/papers/Hassani_Unsupervised_Multi-Task_Feature_Learning_on_Point_Clouds_ICCV_2019_paper.pdf
2. 动机
传统手工设计特征主要捕获局部或全局统计属性,无法表征语义特性。
是否有一个针对需要语义特性这类任务的通用特征呢?
于是本文 提出了一个可以针对非监督多任务模型的特征表达,基于多尺度图的编码器。可端到端训练。
3. 算法
针对三个非监督学习任务:
- 聚类
- 重构
- 自监督分类
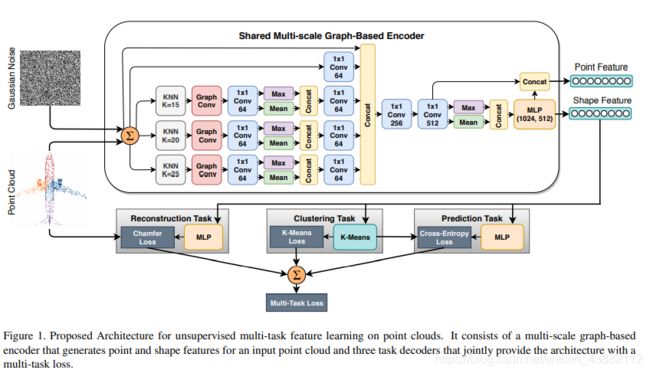
整体框架:
解码器: 多层尺度的(图卷积 + 卷积 + 池化)+ 扰动高斯噪声
本质上适用多任务,也是因为用了这些任务的损失来一起进行训练了,自然有了这个功能。
图卷积定义: 其实就是两个点之间的残差了;
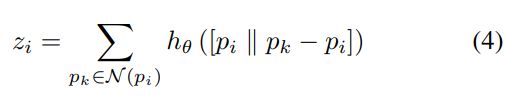
算法描述:
训练集: S = { s 1 , s 2 , . . . , s N } S=\{s_1, s_2, ..., s_N\} S={s1,s2,...,sN},N个点。
一个点: s i = { p 1 i , p 2 i , . . , p M 1 } s_i =\{ p^i_1, p^i_2, .., p^1_M\} si={p1i,p2i,..,pM1}, M个无序点, p j i = ( x j i , y j i , z j i ) p^i_j=(x^i_j, y^i_j, z^i_j) pji=(xji,yji,zji)仅包括坐标
编码器: E θ : S ( R M × d i n ) → Z ( R d z ) E_{\theta}: S (\mathbb{R}^{M\times d_{in}})\rightarrow Z (\mathbb{R}^{d_z}) Eθ:S(RM×din)→Z(Rdz), d z d_z dz 远大于 d i n d_in din
为了学习非监督多任务的 θ \theta θ,设计以下三个参数函数:
聚类函数 T c : Z → y \Tau_c:Z \rightarrow y Tc:Z→y,将隐码归类到 K K K个类别当中,其中 y = [ y 1 , y 2 , . . . , y n ] y=[y_1, y_2, ...,y_n] y=[y1,y2,...,yn], y i ∈ { 0 , 1 } K y_i\in\{0,1\}^K yi∈{0,1}K, 且 y n T 1 k = 1 y^T_n \mathbf{1}_k=1 ynT1k=1。
分类函数 f ψ : Z → y ^ f_\psi: Z \rightarrow \hat{y} fψ:Z→y^, 聚类后的类别预测,换言之,分类函数将隐变量映射到K个预测类 y ^ = [ y 1 ^ , y 2 ^ , . . . , y n ^ ] \hat{y}=[\hat{y_1}, \hat{y_2}, ...,\hat{y_n}] y^=[y1^,y2^,...,yn^],且 y i ^ ∈ { 0 , 1 } K \hat{y_i}\in\{0,1\}^K yi^∈{0,1}K。该函数使用由聚类函数产生的伪标签作为代理训练数据。
解码器函数: g ϕ : Z ( R d z ) → S ^ ( R M × d i n ) g_\phi: Z(\mathbb{R}^{d_z}) \rightarrow \hat{S} (\mathbb{R}^{M\times d_{in}}) gϕ:Z(Rdz)→S^(RM×din),将隐变量重构回点云。如果仅使用聚类损失则会是的特征聚成单类,该函数的设计防止最后聚成了单类。
训练损失:
-
聚类损失: 本质上是在学习聚类中心矩阵: C ∈ R d z × K C\in \mathbb{R}^{d_z \times K} C∈Rdz×K, z n = E θ ( s n ) z_n=E_\theta(sn) zn=Eθ(sn), y n T 1 k = 1 y^T_n\mathbf{1}_k=1 ynT1k=1。其中,初始化 聚类中心矩阵为随机,是epoch更新的。

-
分类损失:交叉熵衡量, y n = T c ( z n ) y_n=\Tau_c(z_n) yn=Tc(zn), y ^ n = f ψ ( z n ) \hat{y}_n=f_\psi(z_n) y^n=fψ(zn)。
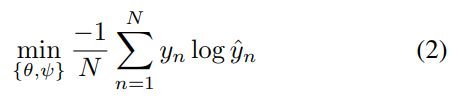
-
重构损失:CD距离。 s ^ n = g ϕ ( z n ) \hat{s}_n=g_\phi (z_n) s^n=gϕ(zn)是重构的点集, s n s_n sn是GT。 N N N:训练集数量; M M M:在每个点集当中的点数量。

最终损失: 上面3个损失的加权求和

4. 实验
模型收敛:88个类,实际55类别。
在分类任务上,非监督与监督方法的比较: 在非监督方法里效果还是不错的;
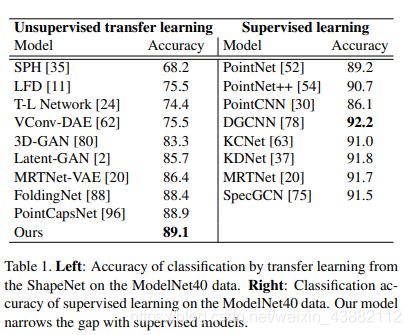
半监督分割任务上的效果: 5%的训练集效果还是挺不错;
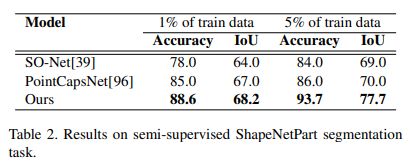
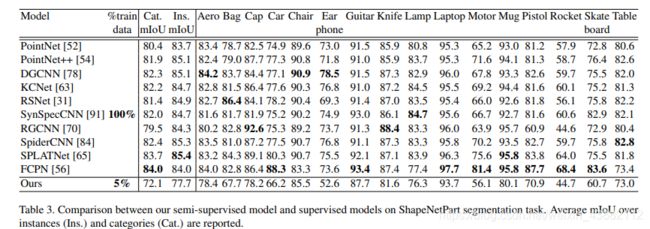
分割任务效果:
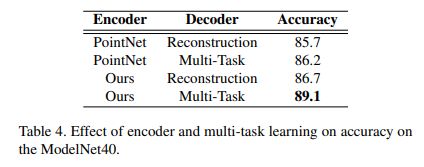
Encoder的作用,在分类任务上进行测试: 其实这里貌似在说,复杂的Encoder对重构后的提升并没有特别大,多类任务的提升是非常大的。
消融实验: 重构任务是关键,加上分类的效果>聚类的效果,因为这里聚类其实也是为了进一步用于分类,实现所谓的非监督。

5.结论及思考
失败案列:
- 适用K-Means来对聚类中心进行初始化,但并没有随机聚类中心方法有所提升;
- 在decoder和分类模型上适用soft共享参数机制,发现效果有所降低,因此将两者分离开来;
- 尝试迭代更多图卷积层,在每一层都重新计算近邻,发现这对分类与分割都不利;

