计算机图形学中需要掌握的数学基础知识有哪些？
计算机图形学中使用了大量数学知识，尤其是矩阵和线性代数。虽然我们倾向于认为3D图形编程是紧跟最新技术的领域之一（它在很多方面确实是），但它用到的很多技术实际上可以追溯到上百年前,其中一些甚至是由文艺复兴时期的伟大哲学家们认识到并记录的。
3D图形学中几乎每个方面、每种效果——移动、缩放、透视、纹理、光照、阴影等，都在很大程度上以数学方式实现。
这里，我们假设读者具备基础的矩阵运算知识。对于基础矩阵代数的完整讲解超出了本书的范围。因此，如果读者在任何时候发现自己不理解特定的矩阵操作，则应当先找一些相关材料阅读，确保完全理解矩阵操作之后再继续学习。
3.1 3D坐标系
3D空间通常用3个坐标轴即x、y和z来表示。这3个坐标轴可以以两种方式布置为左手坐标系或右手坐标系（它们是以坐标轴的朝向来命名的，通过左手或右手大拇指与食指、中指互成直角时各自的指向来进行构造[1]）。3D坐标系如图3.1所示。
图3.1 3D坐标系
知道图形编程环境所使用的坐标系是很重要的。例如，OpenGL中的坐标系大都是右手坐标系，而Direct3D中的坐标系大都是左手坐标系。在本书中，除非特别说明，否则我们都是用右手坐标系。
3.2 点
3D空间中的点可以通过使用形如(2, 8, −3)的符号列出x、y、z的值来表示。不过，如果用齐次坐标—— 一种在19世纪初首次描述的表示法来表示点会更有用。在每个点的齐次坐标有4个值，前3个值表示x、y和z，第四个值w总是非零值，通常为1。因此，我们会将之前的点表示为(2, 8, −3, 1)。正如我们稍后将要看到的，齐次坐标将会使我们的图形计算更高效。
用来存储齐次3D坐标的GLSL数据类型是vec4（“vec”代表向量，同时也可以用来表示点）。GLM库包含适合在C++/OpenGL应用程序中创建和存储含有3个和4个坐标的（齐次）点的类，分别叫作vec3和vec4。
3.3 矩阵
矩阵是矩形的值的阵列，它的元素通常使用下标访问。第一个下标表示行号，第二个下标表示列号，下标从0开始。我们在3D图形计算中要用到的矩阵尺寸常为4×4，如图3.2所示。
图3.2 4×4矩阵
GLSL中的mat4数据类型用来存储4×4矩阵。同样，GLM中的mat4类用以实例化并存储4×4矩阵。
单位矩阵中一条对角线的值为1，其余值全为0：
![\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\\end{matrix} \right]](http://img.e-com-net.com/image/info8/9aa4dc24cd984d3897267f500186b6e1.gif)
任何点或矩阵乘单位矩阵都不会改变。在GLM中，调用构造函数glm::mat4 m(1.0f)可以在变量m中生成单位矩阵。
矩阵转置的计算是通过交换矩阵的行和列完成的。例如：
GLM库和GLSL库都有转置函数，分别是glm::transpose(mat4)和transpose(mat4)。
矩阵加法简单明了：
在GLSL中，“+”运算符在mat4上进行了重载，以支持矩阵加法。
3D图形学中有很多有用的矩阵乘法操作。矩阵乘法一般可以从左向右或从右向左进行（注意，由于左乘和右乘是不同的，所以矩阵乘法不满足交换律）。
在3D图形学中，点与矩阵相乘通常将点视作列向量，并从右向左计算，得到点，如：
注意，我们用齐次坐标将点(X, Y, Z)表示为列数为1的矩阵[2]。
GLSL和GLM都支持点（确切地说是vec4）与矩阵相乘，并使用*操作符表示。
4×4矩阵与4×4矩阵相乘如下：
矩阵相乘也经常叫作合并。稍后我们会看到，它可以用于将一系列矩阵变换合并成一个矩阵。这种合并矩阵变换的能力来自矩阵乘法的结合律。
考虑如下运算序列：
![{\rm NewPoint}={{\bf Matri{{x}}}_{1}}\times \text{ }\!\![\!\!\text{ }{{\bf Matri{{x}}}_{2}}\times ({{{\bf Matri{{x}}}_{3}}}\times {\rm Point})\text{ }\!\!]\!\!\text{ }](http://img.e-com-net.com/image/info8/08ba7efa2f4a4660ba05c56cec7bdcea.gif){kind=small}
我们将点Point与Matrix3相乘，之后将结果与Matrix2相乘，最后将结果与Matrix1相乘，其结果是一个新的点NewPoint。结合律确保了该计算与如下计算结果相同：
我们先将3个矩阵相乘，建立Matrix1、Matrix2、Matrix3的连接。如果我们称其为MatrixC，我们就可以将之前的运算写作：
我们在第4章会看到这么做的好处。我们需要经常将相同的一系列矩阵变换应用到场景中的每个点上。通过预先一次计算好这些矩阵的合并，就可以成倍减少总的矩阵运算量。
GLSL和GLM都支持使用重载后的“*”运算符计算矩阵乘法。
一个4×4矩阵的逆矩阵是另一个4×4矩阵，用M −1表示，在矩阵乘法中有如下性质：
MM-1=M-1M=单位矩阵
在此我们就不展示计算逆矩阵的细节了。但是，需要知道的是计算矩阵的逆矩阵的运算量很大。幸运的是，我们只有很少情况需要用到它。在这些极少的情况下，GLSL和GLM都提供了mat4.inverse()函数。
3.4 变换矩阵
在图形学中，矩阵通常用来进行物体的变换。例如矩阵可以用来将点从一处移动到另一处。在本章中，我们将会学习5个有用的变换矩阵：
- 平移矩阵；
- 缩放矩阵；
- 旋转矩阵；
- 投影矩阵；
- LookAt矩阵。
变换矩阵的重要特性之一就是它们都是4×4矩阵。这是因为我们决定使用齐次坐标系。否则，各变换矩阵可能会有不同的维度并且无法相乘。正如我们所见，确保变换矩阵大小相同并不只是为了方便，同时也为了让它们可以任意组合，预先计算变换矩阵以提升性能。
3.4.1 平移矩阵
平移矩阵A用于将物体从一个位置移至另一位置。它在单位矩阵的基础上，将x、y和z的移动量记录在A03、A13、A23位置。图3.3展示了平移矩阵的形式和它与齐次坐标点相乘的效果。其结果是一个按平移值“移动过”的点。
图3.3 平移矩阵变换
注意，作为与平移矩阵相乘的结果，点(X, Y, Z)平移（或移动）到了位置(X+Tx, Y+Ty, Z+Tz)。同样需要注意的是这个乘法是从右向左计算的。
例如，当我们想要将一组点向上沿y轴正方向移动5个单位，我们可以在单位矩阵的Ty位置放入5来构建平移矩阵。之后我们只需要将我们想要移动的点与矩阵相乘就可以了。
GLM中有一些函数是用于构建与点相乘的平移矩阵的。其中相关的操作有：
- glm::translate(x, y, z)，用于构建位移为(x, y, z)的矩阵；
- mat4*vec4。
3.4.2 缩放矩阵
缩放矩阵用于改变物体的大小或者将点沿朝向或远离原点的方向移动。虽然缩放点这个操作乍一看有点儿奇怪，不过OpenGL中的物体都是用一组或多组点定义的。因此，缩放物体涉及缩放它的点的集合。
缩放矩阵A在单位矩阵的基础上，将位于A00, A11, A22的值替换为x、y、z缩放因子。图3.4中展示了缩放矩阵的形式和它与齐次坐标点相乘的效果，所得的结果是经过缩放的新点。
图3.4 缩放矩阵变换
GLM中有一些函数是用于构建与点相乘的缩放矩阵的。其中相关的操作有：
- glm::scale(x, y, z)，用于构建依照(x, y, z)缩放的矩阵；
- mat4*vec4。
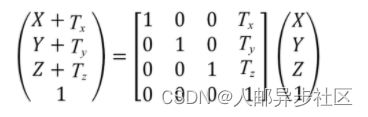
缩放还可以用来切换坐标系。例如，我们可以用缩放来在给定右手坐标系的情况下确定左手坐标系中的坐标。从图3.1中我们可以看到，通过反转z坐标就可以在右手坐标系和左手坐标系中切换，因此，用来切换坐标系的缩放矩阵是：
![\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \\\end{matrix} \right]](http://img.e-com-net.com/image/info8/3871816bf648462083982b3ad28897c6.gif)
3.4.3 旋转矩阵
旋转稍微复杂一些，因为在3D空间中旋转物体需要指定旋转轴和旋转角（以度或弧度为单位）。
在16世纪中叶，数学家莱昂哈德·欧拉表明，围绕任何轴的旋转都可以表示为绕x轴、y轴、z轴旋转的组合[EU76]。围绕这3个轴的旋转角度被称为欧拉角。这个被称为欧拉定理的发现对我们很有用，因为对于每个坐标轴的旋转可以用矩阵变换来表示。
旋转变换有3种，分别是绕x轴、y轴、z轴旋转，如图3.5所示。同时GLM中也有一些用于构建旋转矩阵的函数。其中相关的操作有：
- glm::rotate(mat4, θ, x, y, z)，用于构建绕轴(x, y, z)旋转θ度的矩阵；
- mat4*vec4。
实践中，当在3D空间中旋转轴不穿过原点时，物体使用欧拉角进行旋转需要几个额外的步骤。一般有：
（1）平移旋转轴以使它经过原点；
（2）绕x轴、y轴、z轴旋转适当的欧拉角；
（3）复原步骤（1）中的平移。
图3.5中所示的3个旋转变换都有自己有趣的特性，即反向旋转的矩阵恰等于其转置矩阵。观察这些矩阵，通过cos(−θ) = cos(θ)和sin(−θ) = −sin(θ)即可验证这个特性。后面将会用到这个特性。
图3.5 旋转变换
欧拉角在某些3D图形应用中会导致一些问题。因此，通常在计算旋转时推荐使用四元数。有兴趣探索四元数的读者可以寻求更多已有的资源[KU98]。欧拉角足以满足我们的大部分需求。
3.5 向量
向量表示大小和方向。它们没有特定位置。“平移”向量并不改变它所代表的含义。
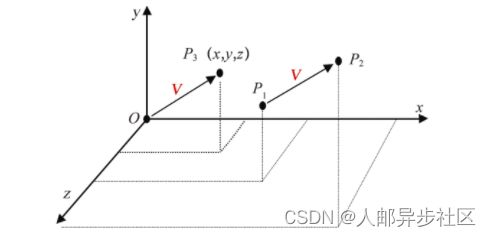
记录向量的方法各式各样，如：一端带箭头的线段、二元组(幅度,方向)，或两点之差。在3D图形学中，向量一般用空间中的单个点表示，向量的大小是原点到该点的距离，方向则是原点到该点的方向。在图3.6中，向量V可以用点P1和P2之间的差表示，也可以等价地用原点到P3来表示。在我们的所有应用中，我们都简单地将V表示为(x, y, z)，即我们用来表示P3的符号。
图3.6 向量V的两种表示
用与表示点相同的方式来表示向量很方便，因为对点和向量可以应用同样的矩阵变换。不过这也会使人困惑。因此，我们有时候会在向量上加一个小箭头（如
）。许多图形系统并不区分点和向量，如GLSL和GLM，它们所提供的vec3和vec4类型既能用来存储点，又能用来存储向量。有的系统（例如本书早期Java版本中所用到的graphicslib3D库）对于点和向量有着不同的类，强制使用适当的类来进行所需的操作。对于点和向量使用同一种类型还是不同的类型哪个更好这件事仍然没有定论。
在GLM和GLSL中有许多3D图形学中经常用到的向量操作。如假设有向量A(u, v, w)和B(x, y, z)，可得如下操作。
加法和减法
A±B = (u±x, v±y, w±z)
GLM: vec3±vec3
GLSL: vec3±vec3
归一化（将长度变为1）
= A/|A| = A/
，其中|A|为向量A的长度
GLM: normalize(vec3) 或normalize(vec4)
GLSL: normalize(vec3) 或normalize(vec4)
点积
A·B = ux + vy + wz
GLM: dot(vec3,vec3) 或dot(vec4,vec4)
GLSL: dot(vec3,vec3) 或dot(vec4,vec4)
叉积
A×B = (vz−wy, wx−uz, uy−vx)
GLM: cross(vec3,vec3)
GLSL: cross(vec3,vec3)
其他有用的向量函数如magnitude()（在GLSL和GLM中是length()）、reflection()和refraction()（在GLSL和GLM中都有）等。
我们现在仔细看一下点积和叉积函数。
3.5.1 点积的应用
本书中的程序大量使用了点积。点积最重要也最基本的应用是求两向量夹角。设向量V和W，计算其夹角θ，则由
有
因此，如果V和W是归一化向量（有着单位长度的向量，这里用“^”标记），则有：
有趣的是，我们后面会看到通常用到的是cos(θ)，而非θ。因此，这两个公式都很有用。
点积同时还有许多其他用途。
- 求向量的大小：
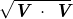。 - 判断两向量是否正交，若正交，则
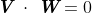。 - 判断两向量是否同向，若同向，则
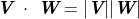。 - 判断两向量是否平行但方向相反，若是，则
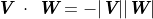。 - 判断两向量夹角是否在−90°～+90°范围内（不包含边界），若是，则
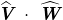>0。 - 求点P=(x, y, z)到平面S=(a, b, c, d)的最小有符号距离。由垂直于S的单位法向量
和从原点到平面的最短距离
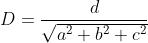，有P到S的最小有符号距离为
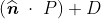，符号由P与S的相对位置决定。
3.5.2 叉积的应用
两向量叉积的一个重要特性是，它会生成一个新的向量，新的向量正交（垂直）于之前两个向量所定义的平面。我们会在本书中大量使用到这一特性。
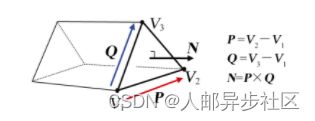
任意两个不共线向量都定义了一个平面。例如，考虑两个任意向量V和W。由于向量可以在不改变含义的情况下进行平移，因此可以将它们移动到起点相交的位置。图3.7展示了V和W定义的平面，以及其叉积所得的该平面的法向量。其所得法向量的方向遵循右手定则，即将右手手指从V向W卷曲会使得大拇指指向法向量R的方向。
图3.7 计算叉积得到法向量
注意，叉积顺序很重要。计算W×V会得到与R方向相反的向量。
通过叉积来获得平面的法向量对我们后面要学习的光照部分非常重要。为了确定光照效果，我们需要知道所渲染模型的外向法向量。图3.8中展示了一个例子，其中有一个由6个点（顶点）构成的简单模型，可使用叉积计算来获得其中一面的外向法向量。
图3.8 计算外向法向量
3.6 局部空间和世界空间
3D图形学（使用OpenGL或其他框架）常见的应用是模拟3D世界、在其中放入物体，并在显示器上观看它。放在3D世界的物体通常用三角形的集合建模。稍后我们会在第6章中详细讲解建模，此处我们可以先了解一下大致的处理过程。
当建立物体的3D模型时，我们通常以最方便的定位方式描述模型。如果模型是球形的，那么我们很可能将球心定位于原点(0,0,0)并赋予它一个易于处理的半径，比如1。模型定义的空间叫作局部空间（local space）或模型空间（model space）。OpenGL官方文档使用的术语是物体空间（object space）。
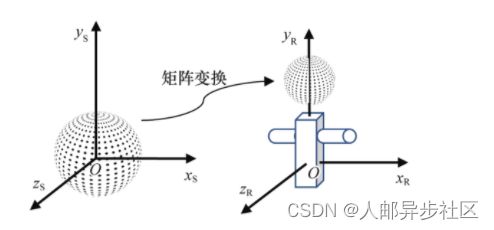
我们刚刚定义的球可能用作一个大模型的一部分，如机器人的头部。这个机器人当然也定义在它自身的局部空间。我们可以用图3.9所示的矩阵变换即通过缩放、旋转和平移，将球放在机器人模型的空间。通过这种方式，可以分层次地构建复杂模型（在4.8节中会进一步通过使用一些矩阵讲解这个主题）。
图3.9 球形和机器人的模型空间
使用同样的方式，通过设定物体在模拟世界中的朝向和大小，可以将物体放在模拟世界的空间中，这个空间叫作世界空间。在世界空间中为对象定位及定向的矩阵称为模型矩阵，通常记为M。
3.7 视觉空间和合成相机
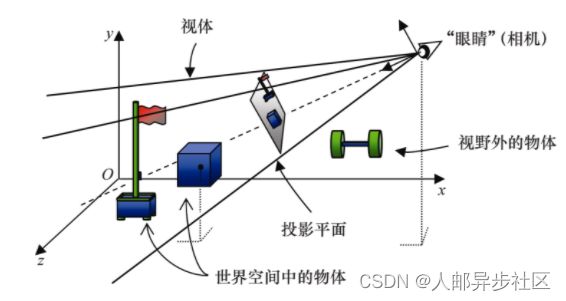
到目前为止，我们所接触的变换矩阵全都可以在3D空间中操作。但是，我们最终需要将3D空间或它的一部分展示在2D显示器上。为了达成这个目标，我们需要找到一个有利点。正如我们在现实世界通过眼睛从一点观察一样，我们也必须找到一点并确立观察方向作为我们观察虚拟世界的窗口。这个点叫作视图或视觉空间，或“合成相机”（简称相机）。
如图3.10和图3.12所示，观察3D世界需要：（a）将相机放入世界的某个位置；（b）调整相机的角度，通常需要一套它自己的直角坐标轴u、v、n（由向量U，V，N构成）；（c）定义一个视体（view volume）；（d）将视体内的对象投影到投影平面（projection plane）上。
图3.10 将相机放入3D世界中
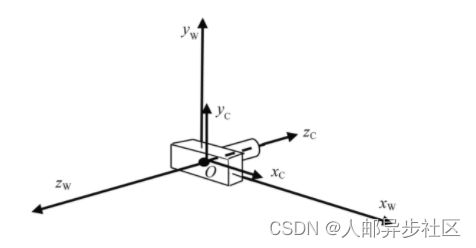
OpenGL有一个固定在原点(0,0,0)并朝向z轴负方向的相机，如图3.11所示。
图3.11 OpenGL固定相机
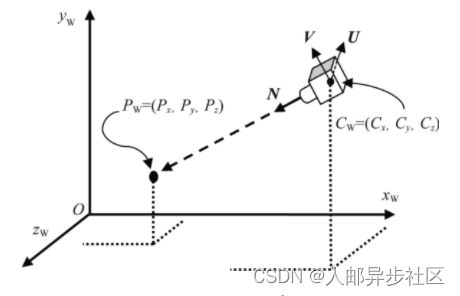
为了应用OpenGL相机，我们需要将它移动到适合的位置和方向。我们需要先找出在世界中的物体与我们期望的相机位置的相对位置（如物体应该在由图3.12所示相机U、V、N向量定义的“相机空间”中的位置）。给定世界空间中的点PW，我们需要通过变换将它转换成相应相机空间中的点，从而让它看起来好像是从我们期望的相机位置CW看到的样子。我们通过计算它在相机空间中的位置PC实现。已知OpenGL相机位置永远固定在点(0,0,0)，那么我们如何变换来实现上述功能？
图3.12 相机方向
需要做的变换如下。
（1）将PW平移，其向量为负的期望相机位置。
（2）将PW旋转，其角度为负的期望相机欧拉角。
我们可以构建一个单一变换矩阵以完成旋转和平移，这个矩阵叫作视图变换（viewing transform）矩阵，记作V。矩阵V合并了矩阵T（包含负相机期望位置的平移矩阵）和R（包含负相机期望欧拉角的旋转矩阵）。在本例中，我们从右向左计算，先平移世界空间中的点PW，之后旋转：
PC = R( TPW )
如前所见，通过结合律我们得到如下运算：
PC = ( RT ) PW
如果我们将合并后的RT存入矩阵V，运算成为：
PC = VPW
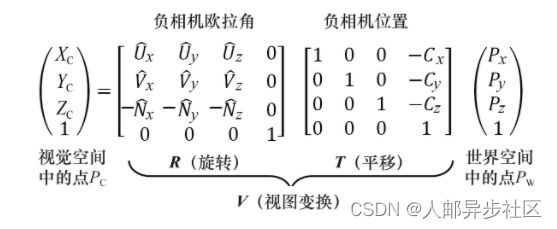
完整的计算以及T和R的具体值在图3.13中（我们忽略了对矩阵R的推导——推导过程见参考资料[FV95]）。
图3.13 推导视图变换矩阵
通常，将V矩阵与模型矩阵M的积定义为模型-视图（Model-View，MV）矩阵，记作MV：
MV = VM
之后，点PM通过如下步骤就可以从自己的模型空间直接转换至相机空间：
PC =MVPM
在复杂场景中，当我们需要对每个顶点，而非一个点做这个变换的时候，这种方法的好处就很明显了。通过预先计算MV，空间中每个点的变换都只需要进行一次矩阵乘法计算。之后，我们会看到，可以将这个过程延伸到更多合并矩阵的计算中，以大量减少点的计算量。
3.8 投影矩阵
当我们设置好相机之后，就可以学习投影矩阵了。我们需要学习的两个重要的投影矩阵：透视投影矩阵和正射投影矩阵。
3.8.1 透视投影矩阵
透视投影通过使用透视概念模仿我们看真实世界的方式，尝试让2D图像看起来像是3D的。物体近大远小，3D空间中有的平行线用透视法画出来就不再平行。
透视法是文艺复兴时期的伟大发现之一，当时的画家借此可以绘制出更加真实的画作。
图3.14所示的画作是一个绝好的例子。它是卡洛·克里韦利在1486年绘制的《圣母领报》（又名《给圣·埃米迪乌斯报喜》，目前收藏于伦敦国家美术馆[CR86]）。这幅画明显强烈地使用了透视法——右侧建筑的左墙的线条戏剧性地向后收束。这种画法让人产生了深度感知和画中有3D空间的错觉。这个过程中，在现实中的一些平行线在画中并不平行。同样，在前景中的人物比在背景中的人物要大。虽然今天我们将这些视为理所当然的，不过算出实现它的变换矩阵还是需要进行一些数学分析的。
图3.14 《圣母领报》（卡洛·克里韦利，1486年）
我们可以通过使用变换矩阵将平行线变为恰当的不平行线来实现这个效果，这个矩阵叫作透视矩阵或者透视变换。可以通过定义4个参数来构建视体：纵横比、视场、近剪裁平面（也称投影平面）、远剪裁平面。
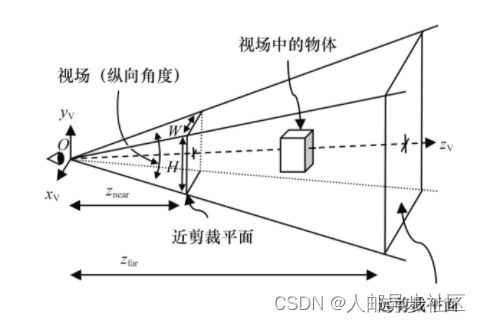
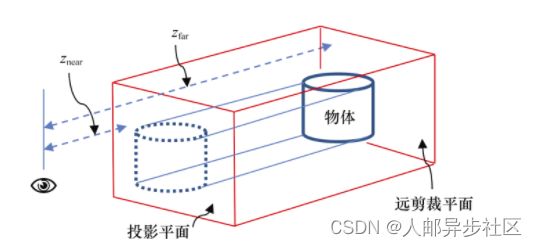
只有在近、远剪裁平面间的物体才会被渲染。近剪裁平面同时也是物体所投影到的平面，通常放在离眼睛或相机较近的位置（如图3.15左侧所示）。我们会在第4章中讨论如何为远（far）剪裁平面选择合适的值。视场（Field Of View，FOV）是可视空间的纵向角度。纵横比（aspect ratio）是远近剪裁平面的宽度与高度之比。由这些参数所决定的形状叫作视体或视锥（view frustum），如图3.15所示。
图3.15 透视视体或视锥
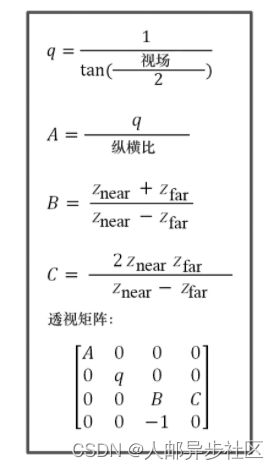
透视矩阵用于将3D空间中的点变换至近剪裁平面上合适的位置。我们需要先计算q、A、B、C的值，之后用这些值来构建透视矩阵，如图3.16所示[FV95]。
图3.16 构建透视矩阵
生成透视矩阵很容易，只需要将所描述的公式插入一个4×4矩阵。GLM库也包含一个用于构建透视矩阵的函数glm::perspective()。
3.8.2 正射投影矩阵
在正射投影中，平行线仍然是平行的，即不使用透视，如图3.17所示。正射与透视相反，在视体中的物体不因其与相机的距离而改变，可以直接投影。
图3.17 正射投影
正射投影是一种平行投影，其中所有的投影过程都沿与投影平面垂直的方向进行。正射矩阵通过指定如下参数构建：（a）从相机到投影平面的距离znear；（b）从相机到远剪裁平面的距离zfar；（c）L、R、T和B的值，其中L和R分别是投影平面左、右边界的x坐标，T和B分别是投影平面上、下边界的y坐标。正射投影矩阵如图3.18所示[WB15]。
图3.18 正射投影矩阵
并非所有平行投影都是正射投影，但是其他平行投影的介绍不在本书范围内。
平行投影的结果与我们眼睛所见到的真实世界不同。但是它在很多情况下都有其用处，比如计算和生成阴影、进行3D剪裁以及计算机辅助设计（Computer Aided Design，CAD）——平行投影用在CAD中是因为无论物体如何摆放，其投影的尺寸都不变。即便如此，本书中绝大多数例子依然使用透视投影。
3.9 LookAt矩阵
我们最后要学习的变换矩阵是LookAt矩阵。当你想要把相机放在某处并看向一个特定的位置时，就需要用到它了，LookAt矩阵的元素如图3.19所示。当然，用我们已经学到的方法也可以实现LookAt变换，但是这个操作非常频繁，因此为它专门构建一个矩阵通常比较有用。
图3.19 LookAt的元素
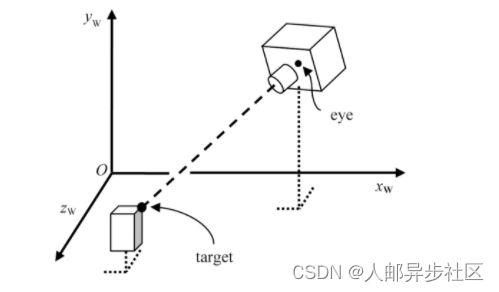
LookAt变换依然由相机旋转决定。我们通过指定大致旋转朝向的向量（如世界y轴）。通常，可以通过一系列叉积获得一组向量，代表相机的正面（向量fwd）、侧面（向量side），以及上面（向量up）。图3.20展示了计算过程，由相机位置（点eye）、目标位置（点target）、初始向上向量Y构建LookAt矩阵[FV95]。
图3.20 LookAt矩阵
我们可以自行将这个过程构建为C++/OpenGL实用函数，但GLM中已经有一个用来构建LookAt矩阵的函数glm::lookAt()，因此我们用它就可以了。稍后在本书第8章生成阴影的时候会用到这个函数。
3.10 用来构建矩阵变换的GLSL函数
虽然GLM包含许多预定义的3D变换函数，本章也已经涵盖了其中的平移、旋转和缩放等函数，但GLSL只包含基础的矩阵运算，如加法、合并等。因此，有时我们需要自己为GLSL编写一些实用函数来构建3D变换矩阵，以在着色器中进行特定3D运算。用于存储这些矩阵的GLSL数据类型是mat4。
GLSL中用于初始化mat4矩阵的语法以列为单位读入值。其前4个参数会放入第一列，接下来4个参数放入下一列，直到第四列，如下所示：
mat4 translationMatrix =
mat4(1.0, 0.0, 0.0, 0.0, // 注意，这是最左列，而非第一行
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
tx, ty, tz, 1.0 );该段代码构建如图3.3所示的平移矩阵。
程序3.1中包含5个用于构建4×4平移、旋转和缩放矩阵的GLSL函数，每个函数对应一个本章之前给出的公式。我们稍后在书中将会用到这些函数。
程序3.1 在GLSL中构建变换矩阵
// 构建并返回平移矩阵
mat4 buildTranslate(float x, float y, float z)
{ mat4 trans = mat4(1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
x, y, z, 1.0 );
return trans;
}
// 构建并返回绕x轴的旋转矩阵
mat4 buildRotateX(float rad)
{ mat4 xrot = mat4(1.0, 0.0, 0.0, 0.0,
0.0, cos(rad), -sin(rad), 0.0,
0.0, sin(rad), cos(rad), 0.0,
0.0, 0.0, 0.0, 1.0 );
return xrot;
}
// 构建并返回绕y轴的旋转矩阵
mat4 buildRotateY(float rad)
{ mat4 yrot = mat4(cos(rad), 0.0, sin(rad), 0.0,
0.0, 1.0, 0.0, 0.0,
-sin(rad), 0.0, cos(rad), 0.0,
0.0, 0.0, 0.0, 1.0 );
return yrot;
}
// 构建并返回绕z轴的旋转矩阵
mat4 buildRotateZ(float rad)
{ mat4 zrot = mat4(cos(rad), -sin(rad), 0.0, 0.0,
sin(rad), cos(rad), 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0 );
return zrot;
}
// 构建并返回缩放矩阵
mat4 buildScale(float x, float y, float z)
{ mat4 scale = mat4(x, 0.0, 0.0, 0.0,
0.0, y, 0.0, 0.0,
0.0, 0.0, z, 0.0,
0.0, 0.0, 0.0, 1.0 );
return scale;
}补充说明
在本章中我们看到了使用矩阵对点进行变换的例子。稍后，我们会将同样的变换应用于向量。要对向量V使用变换矩阵M进行与对点相同的变换，一般需要计算M的逆转置矩阵，记为(M −1)T，并用所得矩阵乘V。在某些情况下，M=(M −1)T，在这些情况下只要用M就可以了。例如，本章中我们所见到的基础旋转矩阵与它们的逆转置矩阵相等，我们可以直接将它们应用于向量（同样也可以应用于点）。因此本书中有时候使用(M −1)T对向量进行变换，有时候仅使用M。
本章中仍未讨论的一种技术是在空间中平滑地移动相机。这是一种很有用的技术，常用于制作游戏和动画电影，同时也适用于可视化、VR和3D建模过程。移动相机的代码叫作相机控制器，关于这个话题在网上有很多资源[TR15]。
我们也没有讲解所有给出的矩阵变换的推导过程[FV95]。相反，我们努力做到简明地总结了基础3D图形学变换中必备的点、向量和矩阵运算。随着本书的推进，我们将会看到本章中方法的许多实际应用。
本文摘自《计算机图形学编程（使用OpenGL和C++）（第2版》中的第3章
使用C++和OpenGL编写图形渲染方法，图形学初级教材，提供模型、图像文件、纹理文件、贴图文件、图表等配套资源，从头实现属于你自己的景色。
本书以OpenGL和C++作为工具，介绍计算机图形学编程的相关内容。全书从图形编程的基础和准备工作讲起，介绍了OpenGL图像管线、3D模型、纹理贴图、光照、阴影、天空和背景、增强表面细节、曲面细分、几何着色器、水面模拟、光线追踪等计算机图形学编程技术。本书各章配备了不同形式的习题，供读者巩固所学知识。
本书适合作为高等院校计算机科学专业的计算机图形编程课程的教材或辅导书，也适合对计算机图形编程感兴趣的读者自学。