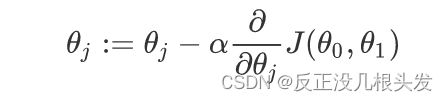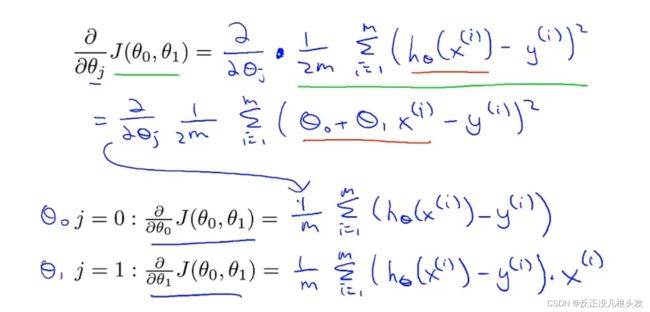吴恩达机器学习视频课笔记【第1-3章】
目录
- 1 机器学习的一些概念
-
- 1.1 基础概念
- 1.2 监督学习
- 1.3 无监督学习
- 1.4 模型的泛化能力
- 1.5 假设空间
- 2 模型相关知识点
-
- 2.1 模型描述
- 2.2 代价函数(cost function)
- 2.3 梯度下降(Gradient descent)
- 2.4 线性回归算法(Linear regression)
- 3 矩阵和向量
- typora使用数学公式(部分)
1 机器学习的一些概念
1.1 基础概念
数据集 data set D={x1,x2,x3,…,xm} 表示含m个示例的数据集
示例 instance 样本 sample
xi={xi1;xi2;xi3;...xid} 指d维样本空间中的一个示例 d称为样本xi的维数(dimensionality)
属性 attribute 特征 feature
属性值 attribute value xij
属性空间 attribute space 样本空间 sample space 输入空间
一个示例对应一个坐标向量--->特征向量(feature vector)
从数据中学得模型的过程(通过学习算法完成):学习(learning) 训练(training)
训练过程使用的数据:训练数据(training data)
每个样本(training sample) 组成的集合(training set)
学得模型:假设(hypothesis) 潜在规律:真相/真实(ground-truth)
模型的实例化:学习器(learner)
标记(label):示例的结果信息
样例(example):拥有标记信息的示例 —>(xi,yi) 第i个样例
yi属于Y Y是所有标记的集合 —> 标记空间(label space) 输出空间
测试样本(testing sample):被预测的样本
1.2 监督学习
(supervised learning):有标记
分类(classification) 预测的是离散值
二分类(binary classification):涉及两个分类 正类(positive class) + 反类/负类(negative class)
多分类(multi-class classification):涉及多个分类
回归(regression) 预测的是连续值
eg:根据已有数据预测房价
测试(testing):学得模型后,使其进行预测的过程 y=f(x)
1.3 无监督学习
(unsupervised learning):无标记
聚类(clustering) 将训练集中的示例分组,每组称为一个“簇”,eg:谷歌新闻
鸡尾酒酒会算法:分离音频
[w,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x’);
SVD函数:singular value decomposition,线性代数常规函数
1.4 模型的泛化能力
泛化能力(generalization):学得模型适用于新样本的能力
分布(distribution)D:样本空间中全体样本服从该分布,每个样本都是独立地从这个分布上采样—>独立同分布
1.5 假设空间
科学推理两大手段:
归纳(induction):泛化(generalization)过程,特殊--->一般 一般性规律
从样例中学习(归纳学习:inductive learning)
概念学习:eg:布尔概念学习(是/不是)
学习过程:在所有假设(hypothesis)组成的空间中进行搜索的过程
(假设空间可能很大,但学习过程一定是基于有限样本训练集进行的,
存在与训练集一致的假设集合--->版本空间(version space))
搜索目标:找到与training set匹配(fit)的hypothesis
搜索策略:
自顶向下:一般--->特殊
自底向上:特殊--->一般
演绎(deduction):特化(specialization)过程,一般--->特殊 基础原理--->具体情况
公理、推导规则--->定理
2 模型相关知识点
2.1 模型描述
Linear regression 线性回归
Hypothesis:hθ(x) = θ0 + θ1*x
θi:模型参数
一些符号:
m:Number of training examples
x:"input" variable / features
y:"output" variable / "target" variable
(x,y) 一个训练样本 one training example
(xi,yi) a specific training example 第i个训练样本
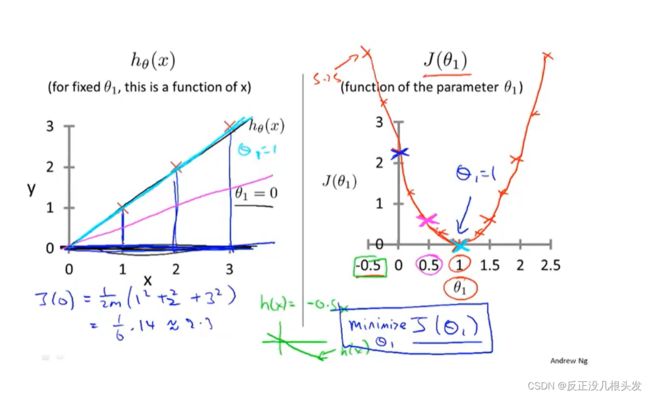
2.2 代价函数(cost function)
选择合适的θ0 、θ1 使得(hθ(x) - y)2 最小minimize:
使得代价函数 (cost function)— 平方误差函数、平方误差代价函数
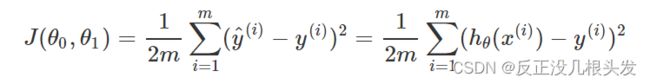
最小
该公式是解决回归问题最常用的手段
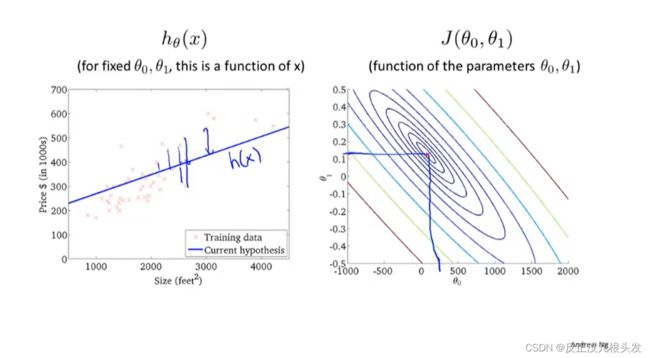
2.3 梯度下降(Gradient descent)
目的:使代价函数 J 最小化
a := b 把b的值赋给a
a = b 判定a和b相等
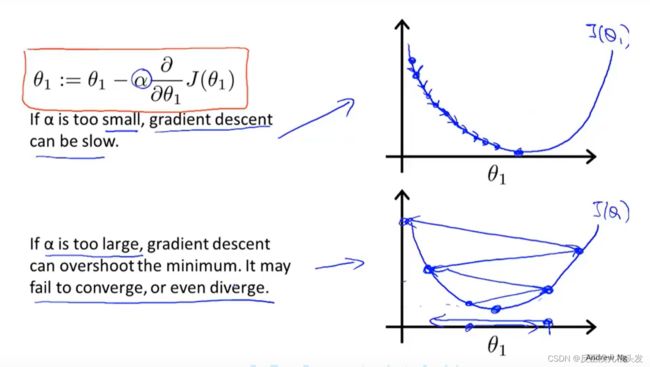
α :学习率(learning rate)梯度下降时,迈多大的步子
α很大时,梯度下降就很迅速
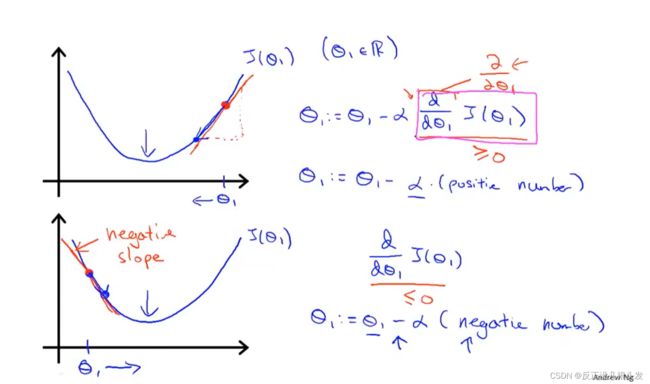
关于学习率 \alpha 的解释:
不能太小,否则拟合得慢
不能太大,否则可能发散
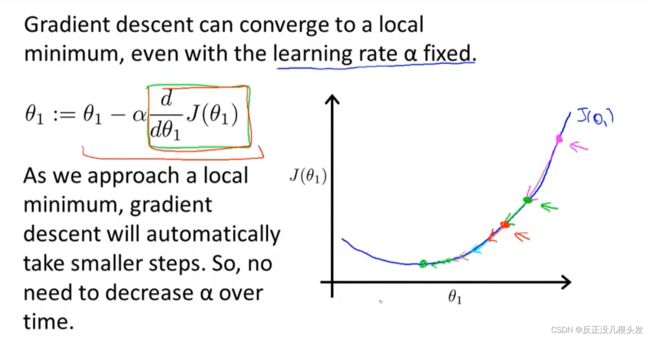
导数部分在接近所要的minimum时也会越来越小,即移动得越来越慢
2.4 线性回归算法(Linear regression)
结合了代价函数 和 梯度下降
计算偏导
带入梯度下降算法
问题:容易陷入局部最优解
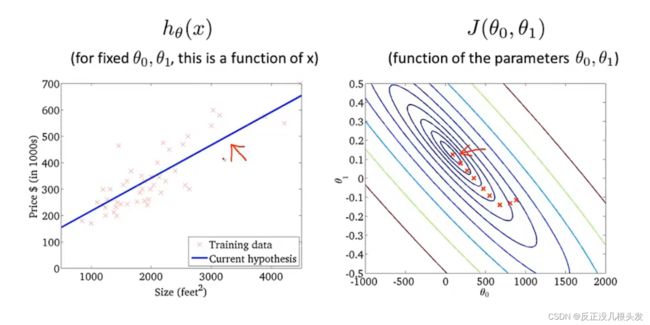
拟合过程
以上:“Batch” Gradient Descent
Batch梯度下降算法:每一步梯度下降,都遍历了整个训练集的样本
后续:正规方程组
3 矩阵和向量
矩阵matrix:大写字母表示
向量vector:小写字母表示,默认下标从1开始,也可以指定从0开始
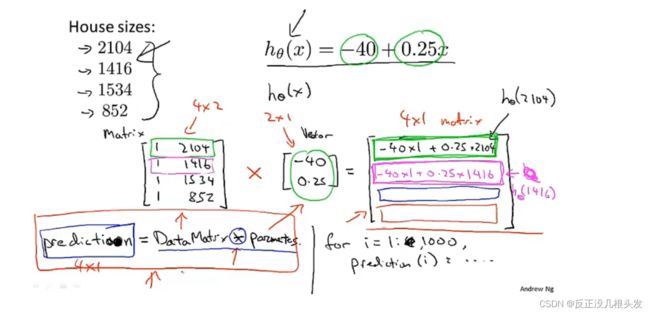
矩阵*向量 实例:预测房价
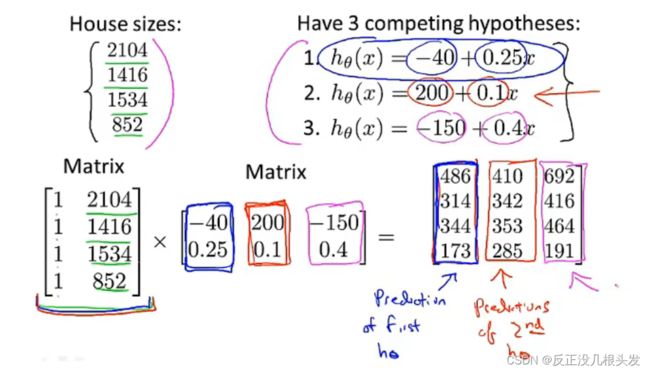
矩阵*矩阵 实例:多种假设下的房价预测
使用python进行矩阵运算
import numpy as np
A = np.array([[3,4],
[2,16]])
B = np.linalg.inv(A) #求A的逆矩阵B
E = np.dot(A,B) #求矩阵A乘矩阵B
奇异矩阵 / 退化矩阵(singular / degenerate):不存在逆矩阵的矩阵
typora使用数学公式(部分)
\frac 分数
\sum 求和
\partial 求偏导
_ 下标
^ 上标