PyTorch自动求导

Autograd模块

PyTorch的Autograd模块是应用所有神经网络的核心内容，在张量（Tensor）上的所有操作，Autograd都能为他们自动提供微分，也就是自动求导的方法，从而简化了手动计算导数的复杂过程。

在0.4之前的版本中，PyTorch通过使用Variable类来自动计算所有的梯度，该类主要包含三个属性：

data：保存Variable所包含的Tensor。
grad：保存data对应的梯度，类型为Variable，形状与data一致。
grad_fn：指向一个Function对象，我们可以通过它使用反向传播计算输入的梯度。
而从0.4版本开始，为了简化使用，PyTorch就将Variable类合并到Tensor中去了，因此我们现在可以直接通过Tensor来使用Autograd模块提供的功能。要使用Autograd，我们只需在创建Tensor时设置属性requries_grad为True即可。一旦我们将requries_grad属性设置为True，就表明我们需要对该Tensor进行自动求导，PyTorch会记录该Tensor的每一步操作历史并自动计算。

requries_grad属性

当我们将requries_grad属性设置为True时，PyTorch会自动追踪和记录对张量Tensor的所有操作，当计算完成后调用backward( )方法自动计算梯度并且将计算结果保存到grad属性中。Tensor进行相关操作后，grad_fn已经被赋予了一个新的函数，这个函数引用了Tensor类的Function对象。Tensor和Function互相连接生成了一个非循环图，它记录并且编码了完整的计算历史。每个张量都有一个grad_fn属性，如果这个张量是用户手动创建的，那么这个张量的grad_fn是None。

自动求导

自动求导使用backward( )函数进行反向传播来计算指定Tensor的梯度，在调用backward( )函数前，Tensor的grad属性为None。

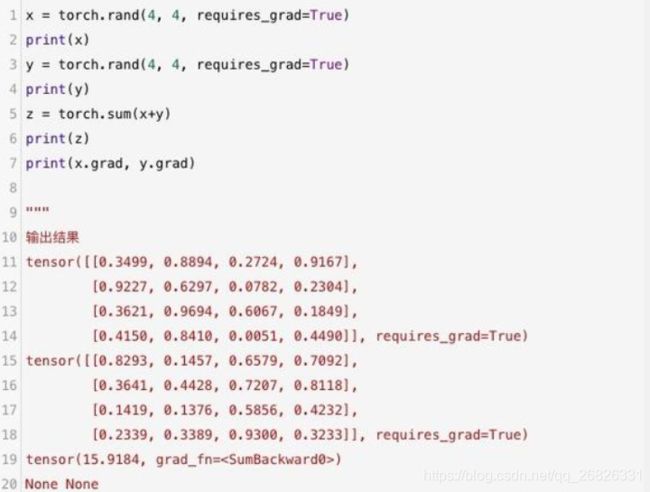
简单的自动求导

如果Tensor表示的是一个标量（只有一个元素的Tensor），则不需要为backward( )指定任何参数，但是如果它有更多的元素，则需要指定一个gradient参数，它是形状匹配的张量。

上述代码中的张量z只有一个元素，因此使用backward( )函数不需要传任何参数。

简单自动求导

以上的z.backward( )相当于是z.backward(torch.tensor(1.))的简写。这种参数常出现在图像分类中的单标签分类，输出一个标量代表图像的标签。

复杂的自动求导

当返回值不是一个标量时，我们在调用backward( )函数时需要传入一个与待自动求导的Tensor大小相同的Tensor作为backward( )函数的参数。

复杂自动求导

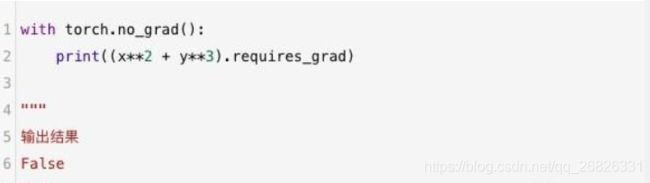
我们可以使用with torch.no_grad()上下文管理器临时禁止对已设置requires_grad=True的张量进行自动求导。这个方法在测试集计算准确率的时候会经常用到，例如：

禁止自动求导

在使用with torch.no_grad()进行嵌套后，PyTorch就不会再跟踪历史记录了，从而释放内存的使用量，同时会加快少许的运算速度。

自动求导原理

要明白自动求导的原理，首先需要知道计算图的概念。

计算图

计算图是现代深度学习框架的核心，为高效自动求导算法——反向传播提供了理论支持。计算图具有如下两个优势：

使用一个简单函数就可以组合成一个极其复杂的模型。
可以实现自动微分（自动求导）。
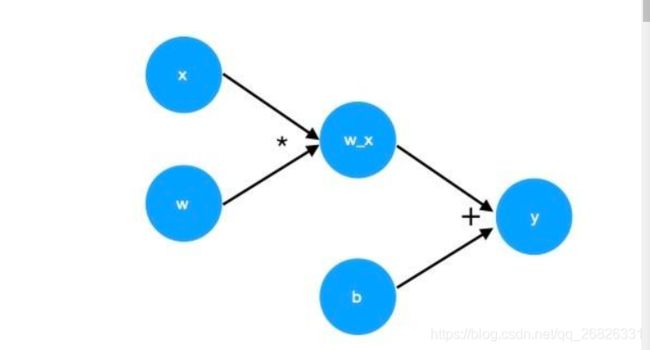
例如对于某个表达式y=wx+b，其中，w、x、b是变量，*、+、=是算子。PyTorch通过记录算子与变量之间的关系可以生成如下图所示的计算图。

自动求导
前向计算图

其中，我们称w、x、b是叶子节点，这些通常是手动创建的、而非运算得到的变量，因此也叫做创建变量。y为根节点，是计算图的最终目标，也就是通过计算后得到的结果，因此也称为结果变量。

判断一个变量是创建变量还是结果变量可以通过Tensor的is_leaf属性获取。例如对于上述代码中的三个张量Tensor：x、y、z，通过访问各自的is_leaf属性可以获取它们的变量属性。

is_leaf属性

x、y为创建变量，z为结果变量。

backward( )实质
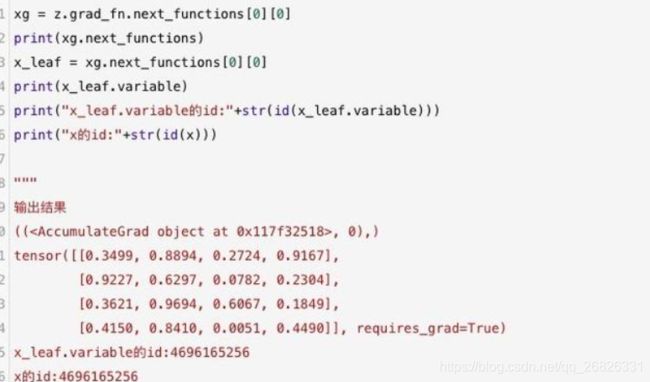
通过上述代码，我们知道执行z.backward( )方法会更新x.grad和y.grad的值，这一点我们可以从grad_fn属性中进行探索，grad_fn记录并编码了整个计算历史。对于z=x2+y3来说，计算结果z的grad_fn为AddBackward0类型的变量，AddBackward0里面有一个next_functions，这个next_functions就是整个grad_fn的精华。

next_functions

打印next_functions可以看到，它是包含两个元素的元组tuple。其中，第一个元素表示x相关的操作记录，第二个元素表示y相关的操作记录。AddBackward0表示的是相加，而这个tuple中的PowBackward0则分别表示x2与y3的操作记录。以x为例，我们继续使用next_functions属性最终得到一个AccumulateGrad。在PyTorch的反向图计算中，AccumulateGrad类型代表的就是叶子节点类型。AccumulateGrad类中有一个variable属性指向叶子节点，这个variable属性就是我们最初的创建变量x。

PyTorch（三）——自动求导
backward( )实质

总结整个backward( )函数的执行过程（以上述代码中的z.backward( )为例）如下：

调用z中的grad_fn属性。
遍历grad_fn的next_functions属性，分别取出其中的Function(AccumulateGrad)，执行求导操作。这个操作是一个递归的过程直到最后类型为叶子节点为止。
将计算结果保存到对应的variable所引用的对象（x和y）的grad属性里。
更新对应变量的grad属性。

backward()对于向量，需要一个参数，这个参数和输出的形状一致。
原因，主要是因为只允许标量对向量求导，才可以得到和输入变量形状相同的导数。
**

详细原因：

参考：https://zhuanlan.zhihu.com/p/29923090

**
variables 和 grad_variables 都可以是 sequence，不过平常也不太有一串变量对另一串变量求导这种需求：如果有这种需求的话，自己写个循环就行了；像 PyTorch 的这个接口，以及 TensorFlow 里提供的求导接口，虽然可以传一堆 x 和一堆 y 进去，但是返回的都是一堆 y 的和对各个 x 的导数，这样一来这个接口的用法就显得很奇怪。反倒不如定义这一堆 y 的和为 z，然后求 z 对各个 x 的导数更加自然。

事实上，TF 和 PyTorch 这么设计不是没有原因的。原因就是： Tensor 没法对 Tensor 求导！举一个简单的例子，如果要求一个 Tensor 对另一个 Tensor 的导数，先考虑矩阵对矩阵这种情形：假设 mn 的矩阵 x 经过运算得到了 pq 的矩阵 y，y 又经过运算得到了 st 的矩阵 z，那么：dz/dy 是啥？假设可以求导，那么得到的应该是四阶张量吧，形状是 stpq？好的，dy/dx 再算一下，得到一个四阶张量 pqm*n。然后怎么反向传播？dz/dx = dz/dy * dy/dx = 两个四阶张量相乘？？？这要怎么乘？？？当然，也不是说绝对不行，仔细思考一下可以把这个问题解决掉，在长度为 p 和 q 的那两个维度上求个和就行，但是想一想无穷无尽的运算组合方式，怎么写一个足够 robust 的反向传播？就算你能解决两个四维 Tensor 怎么乘的问题，Tensor 对标量 Scalar 的导数又是啥？四维和三维的 Tensor 又怎么乘？导数的导数又怎么求，搞一个六阶还是八阶张量做中间结果？这一连串的问题，感觉要疯掉……

一个简单的解决方案就是：

1、不允许 Tensor 对 Tensor 求导，只允许标量 Scalar 对张量 Tensor 求导，求导结果是和自变量同型的 Tensor。

2、在求 dl/dx 的时候（l 是标量，x 是张量），假设有一个中间结果为张量 y，即 x->y->l，那么先求 dl/dy（结果是良定义的、和 y 同型的 Tensor），然后根据 x 和 dl/dy 想办法直接算出 dl/dx，跳过 dy/dx 是啥这种玄学问题！（这种问题在推 MLP 的反向传播时也能遇到，解决办法就是跳过它！）

然后再回到 PyTorch 的设计上来， backward() 为啥还需要一个额外的参数？就是为了避免 Tensor 对 Tensor 求导结果是啥这种玄学问题！torch.autograd.backward(y, w), 或者说 y.backward(w) 的含义是：先计算 l = torch.sum(y * w)，然后求 l 对（能够影响到 y 的）所有变量 x 的导数。这里，y 和 w 是同型 Tensor。也就是说，可以理解成先按照 w 对 y 的各个分量加权，加权求和之后得到真正的 loss，再计算这个 loss 对于所有相关变量的导数。

这么设计有什么好处呢？如前所述，这样一来，所有求导操作都是求 Scalar 关于 Tensor 的导数，统一了起来，不存在 Tensor 对 Tensor 求导了。再回顾一下 PyTorch 自己的文档，它说 torch.autograd.backward 的第二个参数 grad_variables 应该是第一个参数 variables 的对应的导数。

嗯？？这是什么情况？？其实我上面的解释是一致的。假设 y 和 w 是同型 Tensor，那么 l = torch.sum(yw) 对 y 的导数 dl/dy 就是 w。所以把这里的 w 理解成 y 的各项的权重也好，或者理解成某个高高在上的虚拟 loss 对 y 的导数也好，其实是一样的。事实上，l = torch.sum(yw) 这个形式不正好是导数的定义么？数学分析一上来就学，微分是函数增量的线性主部，而在 l = torch.sum(y*w) 这个形式里，只有线性的项，因此 w 就是 dl/dy。

那为什么标量就不需要这个参数呢？假设 y 是标量，然后取 w=1.0，那么 l=torch.sum(y*w) 其实就是 y 本身。所以这时候，dl/dx = dy/dx，可以直接把 loss 和 y 混同，这也就是通常直接把损失函数 loss 当成 y 传进去的原因。