减小模型训练成本的视频动作识别 Efficient Video Transformers with Spatial-Temporal Token Selection 论文精读笔记

写在前面

  好久没写博文了，抽空看了一篇，在准备开题报告相关的事。本文主要来自 VALSE 的一个短视频：20220914【视频理解研究进展与未来】吴祖煊：基于Transformer的视频内容理解，感觉很有意思，遂找到这篇论文来精读下。

• 论文地址：Efficient Video Transformers with Spatial-Temporal Token Selection
• 代码地址：https://github.com/wangjk666/STTS
• 收录于：ECCV 2022

（PS: 关注一下，点个赞呗，主页更多关于多模态视觉问答、实例分割、目标检测，以及如何配置深度学习训练环境，pytorch使用tricks等精彩博文噢！）

一、Abstract

  正常第一段点题：视频 Transformer 计算成本太大了(，图像也大啊)。本文提出基于输入的视频样本动态地选择少量的关键信息 token（源自于时间和空间维度），这个选择依赖于排序得分，其具体实现是一个轻量化的打分网络。针对视频的两个维度，时间维度：和其他方法一样，在空间维度：识别出最具有区分性的区域，而不影响空间位置上下文。由于选择 token 的方式不可微，因此利用一个基于 Top-K 的微分操作：扰动最大值 来进行端到端的训练。

二、引言

  上来讲下视频识别的意义、应用以及现有的方法及其缺陷：训练成本昂贵。点名其来源，Trasformer 结构中的自注意力成本随输入的 tokens 数量成平方项增长，而 tokens 数量又随着输入视频片段中的帧数量线性增长。那么直接抛弃部分tokens不就可以了吗？no，虽然 transformer 对这种丢掉 patch 块的行为不太感冒，但在视频中，简单的扔掉可能会导致空间和时间上 tokens 的不连续，也就破坏了原本的结构化信息。
  之前的方法采用级联的方式来保护空间和时序上的上下文信息。本文认为应该采用 sequential 序列化的方式，即首先关注整个时间轴上的关键帧，然后在这些帧里面查找最重要的空间区域(将图像划分为若干个规则的锚框，进而选出一个锚框)。于是提出了一种轻量化、即插即用的 Spatial-Temporal Token Selection (STTS) 空间时序 Token 选择的方法。
  STTS 主要由一个时序 tokens 选择和一个空间 tokens选择网络组成，每一个网络都是一个多层感知机来预测每个token 的得分。由于这种方法不可微分，因此引入了可微分 Top-K 选择算法并利用扰动最大值方法使得模型能够端到端训练。实验在 Kinetics-400、Something-Something-v2 数据集上进行，Backbone 分别选择 MViT 和 VideoSwim，表现很好。

三、相关工作

3.1 Vision Transformers

  描述一些和 Transformer 的相关工作，主要讲解了 TimeSformer、MViT、VideoSwim 的方法，但这些方法训练成本昂贵。

3.2 Efficient Video Recognition

  指出之前工作的缺点，表明自己的工作第一能打。

3.3 Differentiable Token Selection

  说明一些微分操作是如何进行的，如 Gumbel-Softmax trick。本文应用一种扰动最大值的方法。

四、Spatial-Temporal Token Selection

4.1 回顾 Video Transformers

  和 Image Transformer 差不多，只是输入多加了个 T 维图片帧。

4.2 动态 Token 选择

  将动态 Token 选择视为排序问题：首先采用一个轻量化的打分网络估计出每个输入 token 的分数，然后选择前 $K$ 个得分最高的 token 送入下游预处理。

打分网络

  输入的序列为 $q\in {\mathbb{R}}^{L\times C}$，$L$ 为序列长度，$C$ 为 embedding 维度，采用两个全连接层来输出得分。因此首先将 $q$ 映射到局部表示 ${\text{f}}^1$：
$${\mathbf{f}}^1=\mathrm{FC}\left(\mathbf{q};{\theta }_1\right)\in {\mathbb{R}}^{L\times C^{\prime }}$$其中 ${\theta }_1$ 为网络权重，$C^{\prime }=C/2$。
  接下来在 ${\text{f}}^1$ 基础上得到全局特征表示 ${\text{f}}^g$（这一块没有仔细说明，看代码估计才知道啥情况吧，估摸着是个全局平均池化）。之后在通道维度上拼接 ${\text{f}}^1$ 和 ${\text{f}}^g$：$${\mathbf{f}}_{\mathbf{i}}=\left[{\mathbf{f}}_{\mathbf{i}}^{\mathrm{l}},{\mathbf{f}}^{\mathbf{g}}\right]\in {\mathbb{R}}^{2C^{\prime }}(1\le i\le L)$$
  将 ${\mathbf{f}}_{\mathbf{i}}$ 送入第二个全连接层：
$$\begin{array}{rl}{\mathrm{s}}^{\prime }& =\mathrm{FC}\left(\mathrm{f};{\theta }_2\right)\in {\mathbb{R}}^{L\times 1}\\ \mathrm{s}& =\frac{{\mathrm{s}}^{\prime }-\min \left({\mathrm{s}}^{\prime }\right)}{\max \left({\mathrm{s}}^{\prime }\right)-\min \left({\mathrm{s}}^{\prime }\right)}\end{array}$$其中 ${\theta }_2$ 为网络权重，$\mathrm{s}\in {\mathbb{R}}^L$ 为归一化后的得分。

微分 Top-K 的选择

  从 $\mathrm{s}$ 中选择 $\mathrm{K}$ 个最大得分的 tokens：$\mathrm{y}=\mathrm{Top}-\mathrm{K}(\mathrm{s})\in {\mathbb{N}}^K$，其中 $\mathrm{y}$ 是返回的索引。使用矩阵乘法来加快处理速度，将 $\mathrm{y}$ 转化为一个堆叠 $\mathrm{K}$ 次的 One-hot 编码的 $L$ 维度的向量 $\mathbf{Y}={\left[I_{y_1},I_{y_2},\dots ,I{y}_K\right]}_{\mathrm{m}}\in \{0,1{\}}^{L\times K}$,综合在一起可表示为 ${\mathrm{q}}^{\prime }={\mathrm{Y}}^{\mathrm{T}}\mathrm{q}$。但这一操作是不可微分的，因为 Top-K 和 One-hot 编码不可微。
  因此，采用扰动最大值的方法构建可微分的 Top-K 操作。具体来说，以线性程序的形式选择出 Top-K 个 tokens：$\underset{\mathbf{Y}\in \mathcal{C}}{\mathrm{argmax}}⟨\mathbf{Y},\mathrm{s}{1}^T⟩$，其中 $\mathrm{s}{1}^T$ 为复制 $K$ 次的 $\mathrm{s}$， $\mathcal{C}$ 为凸面体约束集(convex polytope constrain set)，其定义如下：
$$\begin{array}{r}\mathcal{C}=\{\mathbf{Y}\in {\mathbb{R}}^{N\times K}:{\mathbf{Y}}_{n,k}\ge 0,1^{\mathrm{T}}\mathbf{Y}=1,\mathbf{Y}1\le 1,\\ {\sum }_{i\in [N]}i{\mathbf{Y}}_{i,k}<{\sum }_{j\in [N]}j{\mathbf{Y}}_{j,k^{\prime }},\forall k<k^{\prime }\}\end{array}$$

前向传播

  依据期望与随机扰动的关系，对于上面的等式，有：
$${\mathbf{Y}}_{\sigma }={\mathbb{E}}_Z\left[\underset{\mathbf{Y}\in \mathcal{C}}{\mathrm{argmax}}⟨\mathbf{Y},{s1}^{\mathrm{T}}+\sigma \mathbf{Z}⟩\right]$$其中 $\mathbf{Z}$ 为从高斯均匀分布中随机采样得到的噪声向量，$\sigma$ 为控制噪声随机变化的超参数。实际上，运行 Top-K 算法 $n$ 次（实验中设为 500），然后计算 $n$ 个独立样本的期望。

反向传播

  采用雅克比矩阵进行：
$$J_{\mathrm{s}}\mathbf{Y}={\mathbb{E}}_Z\left[\underset{\mathbf{Y}\in \mathcal{C}}{\mathrm{argmax}}⟨\mathbf{Y},{\mathbf{s}}^{\mathrm{T}}+\sigma \mathbf{Z}⟩{\mathbf{Z}}^{\mathrm{T}}/\sigma \right]$$
  训练采用 cross-entropy 损失，端到端方式。在推理过程中，利用 Pytorch 自带的硬 Top-K 选择方式来进一步加快速度。但直接采用这种方式会导致训练—测试时产生性能代沟。为了弥补，根据上式，在训练过程中线性衰减 $\sigma$ 直至为 $0$，当 $\sigma =0$ 时，可微分的 Top-K 操作就等于硬的 Top-K 了，而此时流入打分网络的梯度会消失不见。

4.3 在空间和时序上的实例化

  分开处理空间和时间，让他们分别关注重要的帧和图像上显著的区域。

时序选择

  输入的 tokens 表示为 $\mathrm{X}\in {\mathbb{R}}^{M\times N\times C}$，时序选择的目标是从 $M$ 中选出 $K$ 帧。
  首先在 $\mathrm{X}$ 的空间维度上执行平均池化得到一组基于帧的序列 tokens：${\mathbf{x}}^{\mathbf{t}}\in {\mathbb{R}}^{M\times C}$，之后送入打分网络。经过 Top-K 操作之后得到 $K$ 个最高得分的索引矩阵：${\mathbf{Y}}^{\mathrm{t}}\in {\mathbb{R}}^{M\times K}$。之后，将输入的 $\mathrm{X}$ reshpe 为 $\overline{\mathbf{x}}\in {\mathbb{R}}^{K\times (N\times C)}$，然后使用索引矩阵选择出 $K$ 帧：
$$\overline{\mathbf{z}}={\mathbf{Y}}^{{\mathrm{t}}^{\mathrm{T}}}\overline{\mathbf{x}}\in {\mathbb{R}}^{K\times (N\times C)}$$最后选择出的 tokens 被 reshape为 $\mathbf{Z}\in {\mathbb{R}}^{K\times N\times C}$ 送入接下来的处理步骤中。

空间选择

  对每一帧来说，从 $N$ 个 tokens 中选择 $K$ 个。具体来说，首先将第 $m$ 帧图片 ${\mathrm{x}}_m\in {\mathbb{R}}^{N\times C}$ 喂给打分网络产生得分 ${\mathrm{s}}_m\in {\mathbb{R}}^N$（为简单起见，后续没有下标了）。在空间选择这里并不是直接应用 Top-K，因为这会破坏图像原本的空间结构。因此，引入一种新颖的基于锚框设计的结构：
  在获得每一帧的重要性得分 $$\mathrm{s}\in {\mathbb{R}}^N$ 之后，首先将其 reshape 为 2D 得分图 ${\mathbf{s}}^{\mathbf{s}}\in {\mathbb{R}}^{\sqrt{N}\times \sqrt{N}}$，然后将其划分为一个重叠的锚框尺寸为 $K$ 的网格 ${\tilde{\mathrm{s}}}^{\mathrm{s}}\in {\mathbb{R}}^{G\times K}$，其中 $G={\left(\frac{\sqrt{N}-\sqrt{K}}{\alpha }+1\right)}^2$ 为锚框的数量，$\alpha$ 为步长（图1里面有展示）。之后在每一个锚框内部采用平均池化来获得基于锚框的得分 ${\mathbf{s}}^{\mathbf{a}}\in {\mathbb{R}}^G$，于是原始的 Top-K 选择就被映射为 Top-1 选择的问题了。然后就可以利用 Top-K 操作（此时 $K=1$）来获得矩阵的索引并提取最高得分的锚框了。

五、实验

5.1 实验步骤

Dataset 和 Backbone

  数据集：Kinetics-400、Something-Something-V2 (SSV2)，Backbone：MViT-B16、Video Swin Transformer。$\text{ B- }{\mathrm{T}}_R^L\text{-}{\mathrm{S}}_R^L$ 为不同模型统一表示，其中 $T$、$S$，$L$、$R$ 分别表示时间维度、空间维度的 tokens 选择，tokens 模块被嵌入的位置和选择的 tokens 比例。举个：$\text{ B-}{\mathrm{T}}_{0.4}^0\text{-}{\mathrm{S}}_{0.6}^4$ 表示在第 $0$ 层的 self-attention 之前执行时序 tokens 的选择，选择比例为 $0.4$，在第 $4$ 层的 self-attention 之前执行空间 tokens 的选择，选择的比例为 $0.6$，Backbone 选择 MViT-B16。

评估指标

  top-1 精度、FLOPs。

实施细节

   $\sigma$ 设为 $0.1$，学习率设为 $0.01$。选择 16 帧的视频片段，时序步长为 4，空间尺寸为 $224\times 224$，Batch 64, AdamW 优化器，20个 epochs，前 3 个采用 warm-up 策略。然后是针对各个数据集的具体学习率衰减策略，略过。

5.2 主要结果

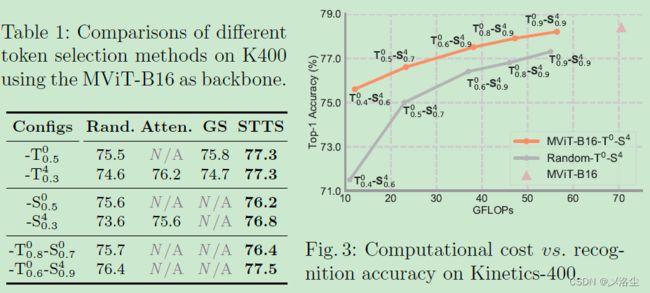
STTS 的效率

与最先进的算法比较

5.3 讨论

在不同位置/步骤上的 Token 选择

基于锚框的空间选择的影响

推理时间

  上表 7，单台 8 卡 3090，(22年10月份估计组装这样一台机器 7W RMB 吧)。

$\sigma$ 的影响

  上表8。

定量分析

结论

本文提出了 STTS，一种动态时序-空间 token 的选择框架，来减小训练数据的冗余。将 tokens 的选择视为一种排序问题，利用 Top-K 操作选出得分最高的前 $\text{K}$ 个 tokens，同时利用扰动最大值的 Top-K 操作使得模型能够端到端训练，实验效果很好。

写在后面

  这篇论文没有给出补充材料哈，不知道作者忘了还是会在下次更新时补上。然后想法也很简单，写作也还可以，值得一看。

  另外，读都读到这里了，麻烦给点个免费赞呗，关注一下，主页更多内容，助力博主持续输出，冲鸭~