模式识别导论大作业(k均值算法,感知器算法,fisher算法,贝叶斯决策,特征提取)
模式识别导论大作业
一、 K均值聚类
1. 功能描述:
利用K-均值算法将150个模式样本分成3类别。分别计算最后算法所用的迭代次数,最终聚类中心以及每个类别中对应模式样本的序号。
2. 带注释的源代码
#include "stdio.h"
#include "math.h"
typedef struct mydata{
float data[4]; //保存原始数据
int index;
}MyData;
MyData myData[150];
float classdata[3][150][4];
int saveindex[3][150]; //保存下表
float center[3][4]; //保存三个聚类中心
float newcenter[3][4];//保存三个新的聚类中心
int findMinCenter(float*temp){//找到当前数据的类别
float dis[3]={0,0,0};
float min = 100000;
int returnk=0;
for(int k=0;k<3;k++){
float mytemp = 0;
for(int m=0;m<4;m++)
mytemp += (temp[m]-center[k][m])*(temp[m]-center[k][m]);
dis[k] = sqrt(mytemp);
//printf("%f\n",dis[k]);
if(dis[k] min = dis[k]; returnk = k; }} return returnk; } void counterNewCenter(floattempdata[][4],int len,int num){ float temp[4] = {0,0,0,0}; //计算新的聚类中心方法 for(int j=0;j for(int i=0;i<4;i++){ temp[i] += tempdata[j][i]; } } for(int k=0;k<4;k++){ newcenter[num][k] = temp[k]/len; printf("k = %f\n",newcenter[num][k]); }} int main(){ int k=0; int kt[3] = {0,0,0}; int i=0,u=0; FILE *fp; if ((fp = fopen("D:\\Iris.txt", "r")) ==NULL){ //打开文件 printf("打开文件失败\n"); return 0; } float numtemp; while (!feof(fp)){ //读取数据 fscanf(fp, "%f", &numtemp); myData[u].data[i++] = numtemp; if(i==4){ u++; i=0;} } fclose(fp);//关闭文件 for(k=0;k<4;k++){ center[0][k] = myData[0].data[k]; center[1][k] = myData[1].data[k]; center[2][k] = myData[2].data[k]; }//设置初始聚类中心 int s=0;int num = 0;i=0;//聚类所用的迭代次数 while(i<150){ i++; k = findMinCenter(myData[i].data); //printf("k = %d\n",k); saveindex[k][kt[k]] = i; for(s=0;s<4;s++){ classdata[k][kt[k]][s] = myData[i].data[s];}//每次将数据分到不同的类中 kt[k]++;if (i == 150){ printf("******************"); for (int m = 0; m<3; m++)//计算新的聚类中心 counterNewCenter(classdata[m],kt[m],m); bool flag = true;//标示前后聚类中心是否相等的布尔类型 for(int n=0;n<3;n++){ for(int t=0;t<4;t++){ if(newcenter[n][t] != center[n][t]){ flag = false; break;}//if if(!flag) break;}//for }//for if(!flag){ i = 0;num++; //如果前后两次的聚类中心不相等,则继续分类 for(int y=0;y<3;y++){ kt[y] = 0; for(int w=0;w<4;w++) center[y][w] = newcenter[y][w];//构建新的聚类中心 }//for }//if(!flag) }//if (i == 150) }//while printf("%d\n",num); //输出聚类所用的迭代次数 if ((fp = fopen("D:\\result.txt", "wr")) ==NULL){ //创建result.txt文件 printf("创建文件失败\n"); return 0; } for(i=0;i<3;i++){ for(u=0;u printf("%d ",saveindex[i][u]);//将3组数据的下标写入文件保存 fprintf(fp,"%d ",saveindex[i][u]); } fprintf(fp,"\n\n\n"); }fclose(fp); return 0; } 聚类所用的迭代次数: 11 第一组: 聚类中心 ( 5.004082 , 3.426531 , 1.463265 , 0.246939 ) 模式样本序号:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 第二组: 聚类中心 (5.883606 , 2.740984 , 4.409837 , 1.434426 ) 模式样本序号:52 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 102 107 114 115 120 122 124 127 128 134 139 143 147 150 第三组: 聚类中心 (6.853845 3.076923 5.715384 2.053846 ) 模式样本序号:51 53 78 101 103 104 105 106 108 109 110 111 112 113 116 117 118 119 121 123 125 126 129 130 131 132 133 135 136 137 138 140 141 142 144 145 146 148 149 文件中共有150个模式样本,要求分成3个模式类别,具体步骤如下: 1. 读取文件中数据,由于样本维数为4。所以建立一个二维组用fscanf格式化读取文件中的样本数据。 2. 选取3个初始样本中心,这里我选择的是样本前三个数据作为初始样本中。用center数据存储。 3. 建立while循环,循环内依次将样本数据按照最短距离原则分类到3个聚类中心中的某一个。这里我用findMinCenter()方法返回当前数据到哪个聚类中心最近的序号。除此之外,用saveindex数组分别记录每个聚类中心中所包含模式样本的序号,方便最后将结果输出。 4. 用counterNewCenter()计算当前类别的新的聚类中心。设置布尔类型的标识flag,初始为true。将3个新的聚类中心,分别和3个原始聚类中心相比较,如有有一个不相同,则设置flag为false,置样本索引i=0,继续循环。否则跳出循环。得到分类结果。 以第一题的分类结果作为样本集,首先选取训练集与测试集(训练集大概是整体样本的2/3),请分别给出三个类别的训练集与测试集包含的样本编号: 第一类训练集样本编号(样本个数26个): 51 53 78 101 103 104 105 106 108 109 110 111 112 113 116 117 118 119 121 123 125 126 129 130 131 132 第二类训练集样本编号(样本个数40个): 52 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 第三类训练集样本编号(样本个数33个): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 第一类测试集样本编号: 133 135 136 137 138 140 141 142 144 145 146 148 149 第二类测试集样本编号: 94 95 96 97 98 99 100 102 107 114 115 120 122 124 127 128 134 139 143 147 150 第三类测试集样本编号: 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 惩罚系数: factor = 0.1 最终计算的得出的权向量为: W1 = (-15.1156 -13.7006 -1.32033 0.448794 -112.199)T W2 = (-34.1219 -19.1983 -14.6433 -3.18996 101.799)T W3 = (-18.77 1.07 -28.8 -10.58 0.5)T 判别函数: D1(X)= -15.1156x1-13.7006x2-1.32033x3+0.448794x4-112.199 D2(X)= -34.1219x1-19.1983x2-14.6433x3+-3.18996x4+101.799 D3(X)= -18.77x1+1.07x2 -28.8x3 -10.58x4+0.5 测试的准确率: 96.0784% 类的类间离散度矩阵: Sb = 类内离散度矩阵: 第一类类内离散矩阵 : 第一类类内离散矩阵: 第一类类内离散矩阵: 测试的准确率: 86.28% 感知器算法通过赏罚原则依据每次对训练集的训练不断修正判别函数的权向量,当分类器发生错误分类的时候对分类器进行“罚”,即对权向量进行修改,当感知器正确分类的时候对分类器进行“赏”,对全向量不进行修改。这样经过迭代计算后,通过训练集的训练得到最优的判别函数的权向量。可以从程序上看出感知器算法的实现是十分简单清晰的,而且对测试集的判断正确率也十分理想,高达96%以上。但是感知器一般只用于小样本数据的学习和识别,对于大样本数据感知器算法就显出劣势了。相对于感知器算法的fisher分类算法在样本的判别正确率上要远低于感知器算法,而且fisher算法的内部实现相对于感知器算法要复杂得多,这大多是由于矩阵计算相当消耗计算机资源。Fisher算法在判别上劣于感知器算法主要是样本的训练集并不能达到fisher算法训练的标准。另一个在样本的不平衡条件下,会导致fisher算法的协方差矩阵不好估计,从而导致矩阵计算的误差。从综合性能和判别结果上分析,感知器算法对于小样本的判别要更适合fisher算法,而且在时间和算法复杂度上都要更好些。 保持第二题中已选择的训练集与测试集不变,将所有的样本从4维降低为两维(随机选取两维),将训练集的所有样本点在二维坐标系下标注出来,注意不同的类别用不同形状的点加以区分。 选取样本的第一维和第二维。 判别函数:d(1)= 42.25*x1 - 4.126*x2+13.19x1*x2-9.01*x2*x2-8.73x1*x1-97.21 d(2)=19.1*x1 + 10.79*x2-2.489x1*x1-6.145x2*x2+3.888x1*x2-70.71 d(3)= 9.813*x1 + 14.42*x2 -1.301x1*x1+5.26x2*x2+2.502x1*x2-5207 判别规则: 如果d(1)>d(2) 且d(1)>d(3)则样本属于第一类 如果d(2)>d(1)且d(2)>d(3)则样本属于第二类 如果d(3)>d(1) 且d(3)>d(2)则样本属于第三类 测试样本个数: 51 错误分类样本个数:9 分类准确率:82.35% 贝叶斯分类决策是通过统计学理论知识中样本的概率问题对样本进行分类判别的。通过样本数据计算样本的后验概率的大小决定样本最终属于的类别。对于正态分布的贝叶斯判别决策更是需要特征空间中某一类样本较多的分布在其均值附近,远离均值样点的个数较少。这样决策才算合理。这使得贝叶斯分类决策十分依赖样本数据。所以对于本实验中4维的数据降到2维,如果选择的维数不同会使得实验结果有较大差距。根据实验结果可以看出某些样本中的两个数据并不能准确的反应这个样本的类别,这导致贝叶斯判别失误。所以在选择样本维数的时候要尽量选择容易区分样本。 2. 特征选择的依据:K-L变换 3. 算法过程: 4. 给定样本X后,首先统计并计算其协方差矩阵CX ; 5. 求CX的特征根,选取前M个最大的特征根对应的特征向量,这些特征向量构成K-L变换的正交阵 ; 6. 对X做K-L变换后得到M维向量Y,作为表示原始样本X的特征 7. 选取样本的第二三维作为数据样本: 判别函数: d(1)=27.59*x1 + 47.52*x2 - 0.5*x1*(8.048*x1 -0.161*x2) + 0.5*x2*(0.161*x1 - 32.51*x2) - 80.46 d(2)= 13.87*x1 + 16.25*x2 + 0.5*x2*(5.176*x1 - 7.096*x2) -0.5*x1*(13.03*x1 - 5.176*x2) - 52.48 d(3)= 15.63*x1 + 10.69*x2 + 0.5*x2*(2.429*x1 - 3.153*x2) -0.5*x1*(9.992*x1 - 2.429*x2) - 52.22 测试样本个数: 51 错误分类样本个数:4 分类准确率: 92.16% 从实验结果来看分类效果还是很理想的,对样本数据进行K-L变换后,再进行贝叶斯分类可以发现样本的分类效果比原来更加高效了。但是K-L最佳变换性能虽好,但实现起来不易。样本不同,协方差矩阵就不同,因此对应的变换T也不一样。为了得到最佳变换,每来一个样本就要重复上述步骤,运算相当繁琐。 通过采集笔、直尺与橡皮长宽高等数据先利用训练集正态分布贝叶斯决策设计判别函数,然后用设计好的分类器对测试样本进行识别分类。 (1).数据采集:通过对笔、直尺与橡皮的图片提取图片中物体的长、宽、高或者界面半径的像素个数。 (2).特征提取: 这里提取样本的长宽比和最小截面面积来作为样本特征数据。其中样本长宽比等于样本长度的像素个数除以样本宽度的像素个数。对于圆形的样本用用截面半径取代样本高度。对最后的样本数据进行归一化。 二维(x1,x2)T,x1表示样本长宽比,x2表示样本最小横截面积 笔 直尺 橡皮 (10.0 , 2.25) (7.0 , 0.3) (1.8 ,6.6) (12.2 , 2.0) (9.4 , 0.25) (2.3 , 8.0) (9.8 , 1.8) (6.0 , 0.4) (1.5 , 4.8) (19.0 , 2.0) (10.5 , 0.32) (2.0 , 5.8) (11.7 , 1.44) (8.5 , 0.34) (3.4 , 4.2) (14.5 , 2.5) (6.2 , 0.5) (2.8 , 3.8) (10.8 , 1.9) (5.8 , 0.28) (1.2 , 5.0) (3).分类器设计:通过正态分布贝叶斯决策对训练集样本进行训练,样本数据为二维(x1,x2)T,x1表示样本长宽比,x2表示样本最小横截面积。计算各个类别的类内散布矩阵和类间散布矩阵。然后获得三个类别的判别函数D(1),D(2),D(3)分别为笔、直尺和橡皮的判别函数。如果D(1)>D(2)&D(1)>D(3),则该样本属于笔;如果D(1)>D(2)&D(1)>D(3),则该样本属于直尺;如果D(1)>D(2)&D(1)>D(3),则该样本属于橡皮。 (4).测试结果: 笔: 100% 直尺: 100% 橡皮: 100% 通过这一个多月的学习,模式识别这门课给我带来的收获还是很多的。特别是这个在完成这个大作业的过程中自己学习到了很多东西。第一个是书本上的理论内容,我梳理了下自己总结的知识点。模式识别过程实际上是计算机通过对采集到的数据进行特征提取后,用模式分类算法构造判别函数(也就是分类器).大作业中有对样本进行分类的k均值算法按最小距离原则依靠聚类中心分类。然后是感知器算法,通过迭代不断修改权向量,最后得到最优的判别函数。Fisher算法对多维数据进行降维处理,找出最优的投影面。贝叶斯决策利用概率论中的知识,通过计算类间离散度和类内离散度,最后得到权向量来判断样本类别。 其次是为了实现算法中复杂的矩阵计算,除了第一题和第二题的第一小问我是用C语言实现的,后面的程序都是用matlab实现的。当然自己也是一边学习一边使用。编程中遇到了很多困难,都是通过百度查询来解决的。经过几天的摸索,虽然不能说写了这几个算法自己就多精通matlab了,但至少自己已经入门,知道怎么用这个强大的科学计算工具来处理复杂的数学问题。 当然学习一门新的语言对学习计算机专业的学生来说并不是什么很难的事情,其实最重要的是弄清书中的算法实现。所以在编写程序之前我总要花几个小时来用心了解书中的理论知识。所以学习这门课也培养我钻研知识的能力,以及培养耐心。因为很多程序总是伴随着很多bug,所以你不得不花大量的时间来调试程序。下面我把自己相关的程序附上作为附录。 作业相关程序: 贝叶斯算法: clc;clear all;d=2;c=3;N=50;errnum = 0;N1=33;N2=40;N3=26; p1 = N1/N;p2 =N2/N;p3=N3/N;D=load('Iris_data.txt'); data=zeros(150,d);G1=zeros(N1,d);G2=zeros(N2,d);G3=zeros(N3,d); hG1=zeros(50-N1,d);hG2=zeros(50-N2,d);hG3=zeros(50-N3,d); data(:,1)=D(:,2); data(:,2)=D(:,4); for i=1:1:N1 G1(i,:)=data(i,:);end for i=1:1:N-N1 hG1(i,:)=data(i+N1,:);end for i=1:1:N2 G2(i,:)=data(N+i,:);end for i=1:1:N-N2 hG2(i,:)=data(N+N2+i,:);end for i=1:1:N3 G3(i,:)=data(2*N+i,:);end for i=1:1:N-N3 hG3(i,:)=data(2*N+N3+i,:);end miu1=mean(G1,1)miu2=mean(G2,1)miu3=mean(G3,1) sigma1=zeros(d,d);sigma2=zeros(d,d);sigma3=zeros(d,d); for i=1:1:N1 sigma1=sigma1+(G1(i,:)-miu1)'*(G1(i,:)-miu1); end for i=1:1:N2 sigma2=sigma2+(G2(i,:)-miu2)'*(G2(i,:)-miu2);end for i=1:1:N3 sigma3=sigma3+(G3(i,:)-miu3)'*(G3(i,:)-miu3);end sigma1=sigma1/N1;sigma2=sigma2/N2;sigma3=sigma3/N3; R=zeros(150,3);syms x1 x2 positive; temp = [x1 x2];format short; d1=log(p1)-1/2*log(det(sigma1))-1/2*(temp*inv(sigma1)*temp')+miu1*inv(sigma1)*temp'-1/2*miu1*inv(sigma1)*miu1'; d2=log(p2)-1/2*log(det(sigma2))-1/2*(temp*inv(sigma2)*temp')+miu2*inv(sigma2)*temp'-1/2*miu2*inv(sigma2)*miu2'; d3=log(p3)-1/2*log(det(sigma3))-1/2*(temp*inv(sigma3)*temp')+miu3*inv(sigma3)*temp'-1/2*miu3*inv(sigma3)*miu3'; fun1 =@(temp)(log(p1)-1/2*(temp-miu1)*inv(sigma1)*((temp-miu1)')-1/2*log(det(sigma1))); fun2 =@(temp)(log(p2)-1/2*(temp-miu2)*inv(sigma2)*((temp-miu2)')-1/2*log(det(sigma2))); fun3 =@(temp)(log(p3)-1/2*(temp-miu3)*inv(sigma3)*((temp-miu3)')-1/2*log(det(sigma3))'); sd1 = vpa(d1,4);sd2 =vpa(d2,4);sd3 = vpa(d3,4); format shortaxis([0,13,1.8,14]); for i=1:1:N-N1 hold on x1= data(i+N1,1); x2= data(i+N1,2); if fun1([x1,x2])>fun2([x1,x2])&&fun1([x1,x2])>fun3([x1,x2]) scatter(x2,x1,40,'r','v','filled');else scatter(x2,x1,40,[0.3,0,0],'v','filled'); errnum = errnum+1;end end for i=1:1:N-N2 hold on x1= data(i+N2+N,1); x2 = data(i+N2+N,2); if fun2([x1,x2])>fun1([x1,x2])&&fun2([x1,x2])>fun1([x1,x2]) scatter(x2,x1,40,'b','^','filled'); else scatter(x2,x1,40,[0,0,0.3],'v','filled'); errnum = errnum+1; end end for i=1:1:N-N3 hold on x1 = data(i+N3+2*N,1); x2 = data(i+N3+2*N,2); if fun3([x1,x2])>fun1([x1,x2])&&fun3([x1,x2])>fun2([x1,x2]) scatter(x2,x1,40,'g','o','filled');else scatter(x2,x1,40,[0,0.3,0],'o','filled'); errnum = errnum+1;end end errnum fisher算法: num1= 26;num2 = 40; num3=33;sum=num1+num2+num3; p1 =num1/sum;p2=num3/sum;p3=num3/sum; temp = [0,0]; for i=1:length(data1) temp = temp+data1(i,:); end meandata1 =temp/length(data1); meandata1'temp = [0,0]; for i=1:length(data2) temp = temp+data2(i,:);end meandata2 = temp/length(data2); meandata2' temp = [0,0];for i=1:length(data3) temp = temp+data3(i,:);end meandata3 = temp/length(data3); meandata3' S1 = zeros(2);S2 = zeros(2);S3 = zeros(2); for i=1:length(data1) S1 =S1+(meandata1-data1(i,:))'*(meandata1-data1(i,:));end for i=1:length(data2) S2 =S2+(meandata2-data2(i,:))'*(meandata2-data2(i,:));end for i=1:length(data3) S3 =S3+(meandata3-data3(i,:))'*(meandata3-data3(i,:));end Sw = S1+S2+S3; meandata0= meandata1*p1+meandata2*p2+meandata3*p3; Sb =(meandata1-meandata0)'*(meandata1-meandata0)*p1+...(meandata2-meandata0)'*(meandata2-meandata0)*p2+(meandata3-meandata0)'*(meandata3-meandata0)*p3;W= Sw\Sb; ins1 = W\S1*W;ins2 =W\S2*W;ins3 = W\S3*W; 、 3. 分类结果
4. 算法分析
二、 线性分类器设计(20分)
1. 设定分类规则(一对多还是一对一),并利用迭代法在训练集上设计线性分类器(给出惩罚系数),给出判别函数。同时将测试集中的数据代入判别函数,给出测试的准确率;
2. 设定分类规则(一对多还是一对一),并利用Fisher法在训练集上设计线性分类器,给出判别函数(给出各类的类间离散度矩阵与类内离散度矩阵等参数)。同时将测试集中的数据代入判别函数,给出测试的准确率;
3. 对上述的两种算法进行分析
三、 贝叶斯决策(20分)
1. 利用贝叶斯决策与训练集设计分类器,写出判别函数与判别规则。
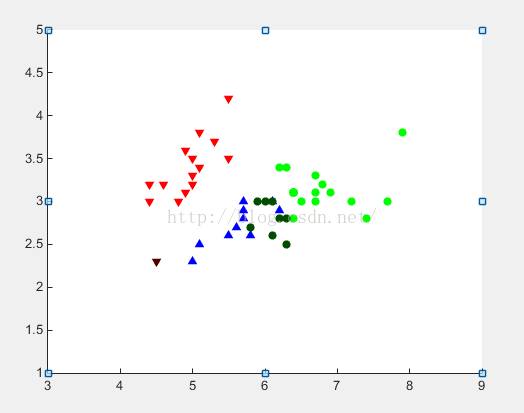
2. 将判别函数作用于测试集,在二维坐标系下将测试集的数据标注出来,注意不同的类别用不同形状的点加以区分,用深浅不同的灰度表示错分与正确分类的样本点,给出分类的准确率。
3. 实验结果分析
四、 特征选择(20分)
1. 保持第二题中已选择的训练集与测试集不变,利用特征选择算法,将样本从4维特征空间降至2维特征空间。给出特征选择的依据与算法过程。并将训练集的所有样本点在二维坐标系下标注出来,注意不同的类别用不同形状的点加以区分。
9. 依然利用贝叶斯决策和训练集设计分类器,写出判别函数。
10. 将判别函数作用于测试集,在二维坐标系下将测试集的数据标注出来,注意不同的类别用不同形状的点加以区分,用深浅不同的灰度表示错分与正确分类的样本点,给出分类的准确率
实验结果分析
五、 系统设计(12分)
1. 任务描述:设计一个模式识别系统,可以识别笔、直尺与橡皮。
2. 基本要求:按照统计类模式识别的基本步骤,从数据采集开始,到特征提取、分类器设计,直至测试结果,给出每一步的具体实现过程。
六、 心得体会(8分)