神经网络学习笔记(2)——代价函数与梯度下降简介
同样的,这篇还是纯理论,不涉及代码部分。
有些地方我也没有深究,所以有可能会有错误,如有错误,请麻烦指正。
目录
- 代价函数
- 梯度下降
-
- 梯度
-
- 偏导数
- 方向导数
- 公式:
- 参考
结合 上篇文章的内容,我们不妨来想一下,在最开始的时候,整个网络是混乱的,那么我们要怎样才能找到最合适的权重和偏置呢?
由于神经网络是需要学习的,所以学习的过程就是找到最合适的权重和偏置。于是我们就要引入代价函数。
代价函数
继续借用3B1B的栗子,假设我们输入的图片是手写的3,想要获得的结果是3,输出层灰度值与期望值如下:

代价(cost)也称作损失(loss),指的是输出层所有输出的激活值与想要的值之间的差的平方求和。如上图所示的情况,那么代价如下:
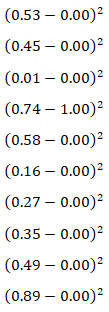
而经验风险(Empirical Risk)就是将所有的代价的算术平均值,我们通过这个平均值来衡量整个网络的好坏。平均值越小,说明网络越接近真实情况,平均值越大就说明网络越离谱。
那么我们肯定希望能够找到一个方法来使经验风险越小越好,而怎样才能找到这个最小值?是不是我们可以用一阶偏导数来解决这个问题?于是我们引入梯度下降这个概念。
梯度下降
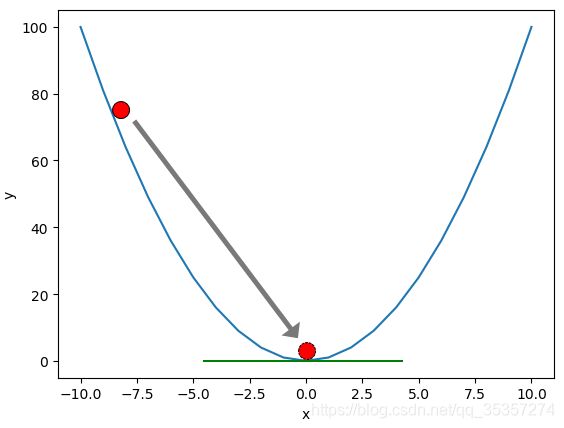
如上图,是一个 y = x 2 y = x^2 y=x2的图像,假设我们的代价函数图像如上图,而我们的经验风险值最开始位于实线的小圆圈这里,为了使经验风险最低,那么这个球就一直滚啊滚,滚到了坑里面,这时候导数为0,说明取到了极值点,这时候经验风险也是最低的。
但是由于上图只是个一元二次方程,但是实际情况中肯定图像会很复杂,同时也会有许多坑位,所以对于梯度下降而言,我们只能取的局部最优解,如下图:

(原谅我懒得写函数直接画了个sin哈哈哈),对于这么一个复杂的情况而言,无论是红色还是蓝色的小球都会滚到合理的坑位,如果我们假设要把右边的红球滚到右边的坑位里面(假设右边坑位是全局最优解),那么我们可以想象一下这个带来的性能损耗有多大,就等于说对于每一个权重和偏置,都要遍历整个网络节点一遍,然后取到最优值,然后有可能某个权重或偏置的改变,又会影响到另外一些权重或偏置。或者就从物理角度上想,把它搬到山顶是不是要多做功呀?
有了梯度下降的感受后,我们来讲一下什么是梯度:
梯度
这一部分我浅尝辄止的讲一下,因为没有太过于深究这部分的内容
偏导数
先来说一下什么是偏导数,先看下图:

(这张图是网上嫖的……),偏导数的意思就是,对某个变量求导,将其他的变量看做常量。就比如上图如果我们对x求偏导 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z,那么实际上就是粉色那条线上的导数,同理 ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z就是红色那条线(线条可以自行移动,毕竟x或y是被看做常量的了,只需要是直线就行)。
接着我们来说下方向导数:
方向导数
方向导数指的是在函数定义域的内点,对某一方向求导得到的导数。表达出来为: ∂ f ∂ l = ∂ f ∂ x cos α + ∂ f ∂ y cos β \frac{\partial f}{\partial l} = \frac{\partial f}{\partial x}\cos\alpha + \frac{\partial f}{\partial y}\cos\beta ∂l∂f=∂x∂fcosα+∂y∂fcosβ,每多一个变量,后面就多跟一个偏导乘方向角就行。
当方向角都为 π 2 \frac{\pi}{2} 2π时,即cos为0时,这时就位于等值线上,超这方向移动的话不会带来函数值的改变;当方向角为 0 0 0时,这时候cos为1,此时上升最快,即梯度;当方向角为 π \pi π时,这时候cos为-1,此时下降最快,即梯度下降。
关于方向导数这一块更深入的内容大家可以看小元老师讲的视频,梯度直观化的动画可以看这个视频。
最后就是关于梯度和梯度下降的公式:
公式:
以二元为例,梯度: g r a d f ( x , y ) = ∇ f ( x , y ) = { ∂ f ∂ x , ∂ f ∂ y } = f x ( x , y ) i ⃗ + f y ( x , y ) j ⃗ gradf(x,y) = \nabla f(x,y) = \{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\} = f_x(x,y)\vec i + f_y(x,y)\vec j gradf(x,y)=∇f(x,y)={∂x∂f,∂y∂f}=fx(x,y)i+fy(x,y)j,这里 i ⃗ \vec i i是x轴的单位向量, j ⃗ \vec j j是y轴的单位向量。
由于梯度是上升最快的方向,所以梯度下降下降最快的路,也就是加个负号,公式为: − g r a d f ( x , y ) = − ∇ f ( x , y ) = − { ∂ f ∂ x , ∂ f ∂ y } = − ( f x ( x , y ) i ⃗ + f y ( x , y ) j ⃗ ) -gradf(x,y) = -\nabla f(x,y) =- \{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\} = -(f_x(x,y)\vec i + f_y(x,y)\vec j) −gradf(x,y)=−∇f(x,y)=−{∂x∂f,∂y∂f}=−(fx(x,y)i+fy(x,y)j)
参考
[1]3Blue1Brown.【官方双语】深度学习之梯度下降法 Part 2 ver 0.9 beta[EB/OL].https://www.bilibili.com/video/BV1Ux411j7ri,2017-11-8.
[2]小元老师高数线代概率.60_1方向导数与梯度,爬山去,用梯度?【小元老师】高等数学,考研数学[EB/OL].https://www.bilibili.com/video/BV1ax411S7Bb?t=2219,2017-4-10.
[3]遇见数学.动画带你理解偏导数和梯度 Gradients and Partial Derivatives(Physics Videos)熟肉[EB/OL].https://www.bilibili.com/video/BV1sW411775X,2018-2-21.