关于Tensorflow中BATCH_SIZE,CELL_SIZE的讨论

本文转载自：https://zhuanlan.zhihu.com/p/31941650

这几天在看莫凡老师Tensorflow（以下简称TF）视频，被几个SIZE搞晕了，看了些资料，说说自己的理解，也和大家讨论一下。本人TF小白，还在学习中，请各位多多指教。

本文内容都是个人的一些观点，如有误，请及时指出，谢谢

话不多说，开始撸：

首先TF的几个关键的SIZE：

1. INPUT_SIZE：输入数据维度
2. OUTPUT_SIZE：输出数据维度
3. BATCH_SIZE：批次大小，也即每次训练输入数据的个数
4. TIME_STEPS：BPTT传播的时间层数，程序中也为n_step
5. CELL_SIZE：隐藏层状态变量State的维度，或为STATE_SIZE

上面提到的几个SIZE，1和2相信大家能理解，关键在于3-5。

为此，我以莫凡老师RNN LSTM (回归例子)代码为基础，借助用LSTM预测股票每日最高价这个例子聊一聊这几个SIZE到底咋回事。

股票数据部分截图

CASE :

选取x和y各1000个作为训练数据，其中INPUT_SIZE=7，OUTPUT_SIZE=1。

设置BATCH_SIZE=1，TIME_STEPS=1000，CELL_SIZE=9。

（选择这些奇数是为了方面观察）

讨论：

首先声明，BATCH_SIZE * TIME_STEPS 必须等于数据长度，即1000；如果你取BATCH_SIZE=20，那么TIME_STEPS=50。

• TF的初始化

with tf.name_scope('inputs'):
    self.xs = tf.placeholder(tf.float32, [None, n_steps, input_size], name='xs')
    self.ys = tf.placeholder(tf.float32, [None, n_steps, output_size], name='ys')

输入x的shape为[None, n_steps, input_size]，即[1,1000,7]

输出y的shape为[None, n_steps, output_size]，即[1,1000,1]

• 输入层

def add_input_layer(self,):
   l_in_x = tf.reshape(self.xs, [-1, self.input_size], name='2_2D')
   Ws_in = self._weight_variable([self.input_size, self.cell_size])
   bs_in = self._bias_variable([self.cell_size,])
   with tf.name_scope('Wx_plus_b'):
       l_in_y = tf.matmul(l_in_x, Ws_in) + bs_in
   self.l_in_y = tf.reshape(l_in_y, [-1, self.n_steps, self.cell_size], name='2_3D')

将x转换为[-1,input_size]，[1000,7]

权重w的shape为：[input_size, cell_size]，即[7,9]

偏执b的shape为：[cell_size]，即[9]

计算公式为：xW+b=y，shape计算为：[1000,7]*[7,9]=[1000,9]

所以y的shape为[1000,9]

输出时，将y转换为[-1, n_steps, cell_size]，即[1,1000,9]

• 隐藏层

def add_cell(self):
   lstm_cell = tf.contrib.rnn.BasicLSTMCell(self.cell_size, forget_bias=1.0, state_is_tuple=True)
   with tf.name_scope('initial_state'):
       self.cell_init_state = lstm_cell.zero_state(self.batch_size, dtype=tf.float32)
   self.cell_outputs, self.cell_final_state = tf.nn.dynamic_rnn(
       lstm_cell, self.l_in_y, initial_state=self.cell_init_state, time_major=False)

从输入层传过来的数据shape为[-1, n_steps, cell_size]

也可表示为[batch_size, n_steps, cell_size]

用数字代替就是[1,1000,9]

batch_size 为每一次训练输入X的个数（X的shape为[batch_size, cell_size]=[1,9]）

n_steps 可以理解为隐藏层神经元的数量；

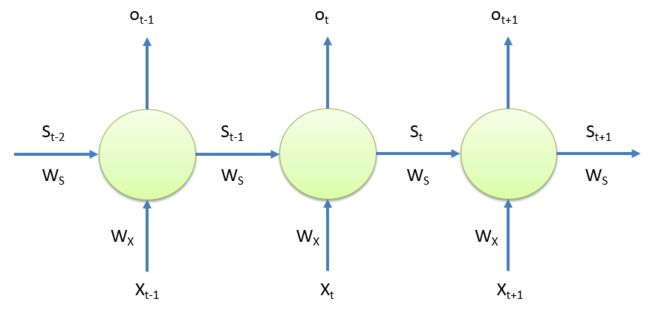
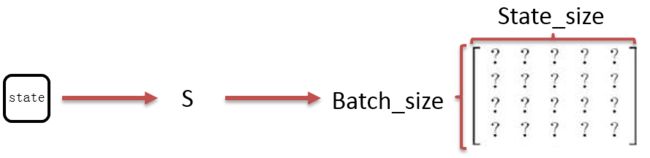
cell_size 实际上就是state_size，就是下图中S的维度；

RNN的隐藏层

对于每一个神经元：

隐藏层的S的shape为[batch_size, cell_size]，即[1,9]

权重Ws和Wx的shape都为[cell_size, cell_size]，即[9,9]

输出Ot的shape为[batch_size, cell_size]，即[1,9]

对于整个隐藏层而言，由于有1000个神经元，则shape为[batch_size, n_steps, cell_size]，即[1,1000,9]

• 输出层

def add_output_layer(self):
   l_out_x = tf.reshape(self.cell_outputs, [-1, self.cell_size], name='2_2D')
   Ws_out = self._weight_variable([self.cell_size, self.output_size])
   bs_out = self._bias_variable([self.output_size, ])
   with tf.name_scope('Wx_plus_b'):
       self.pred = tf.matmul(l_out_x, Ws_out) + bs_out

输入数据转换[batch_size, n_steps, cell_size]—> [-1, cell_size]

即[1,1000,9]—>[1000,9]

权重w的shape为[cell_size, output_size]，即[9,1]

偏执b的shape为[output_size]，即[9]

计算公式为：xW+b=y，shape计算为：[1000,9]*[9,1]+[1]=[1000,1]

总结一下：

time_steps或者n_steps： BPTT传播的时间层数；

batch_size： 就是批次大小；

cell_size或者state_size： 就是隐藏层数据的维度，可自己设定。

补充：

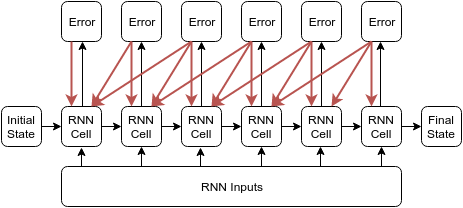
这里讨论一下batch_size，time_steps和state_size名称的由来，用莫凡视频中提到的文章Styles of Truncated Backpropagation 中的图片讨论。

刚才我们假设batch_size=1就和上面这张图的效果类似。上图中，我们假设RNN Inputs包含6个x，并且被分在一个batch中，所以batch_size=1；RNN Inputs中每1个x都有一个神经元与其对应， BPTT传播时可从第6层传播到第1层，一共6层，所以time_steps=6；另一方面，也可以通过batch_size*time_steps来确认一下。

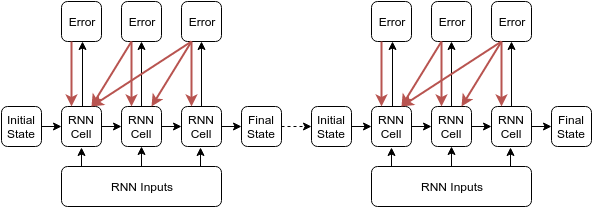
我稍微做一下修改：

和刚才一样，我们假设RNN Inputs包含6个x，但是他被分成了两个独立batch，所以batch_size=2；每个batch里面包含3个x,，BPTT传播时可从第3层传播到第1层，一共3层，所以time_steps=3；同样，也可以通过batch_size*time_steps来确认一下。

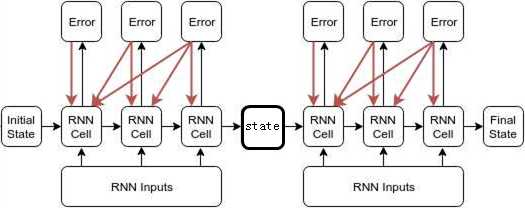
cell_size和state_size，怎么说呢，反正就是上图右边那个矩阵的维度。

如果你把上图左边的方框当作state，他就叫state_size；

如果你把上图左边的方框当作cell，他就叫cell_size。

整体上看：

time_steps因为跟时间层有关，所以叫time_steps；

batch_size因为表示分批个数，所以叫batch_size。

cell_size可以自己设定一个数，具体怎么取，取多少，我还不知道。