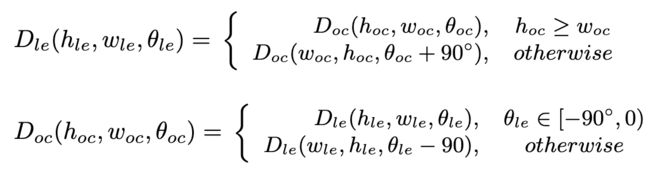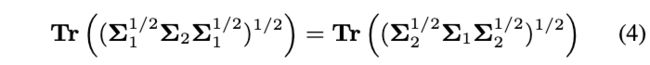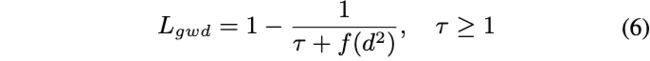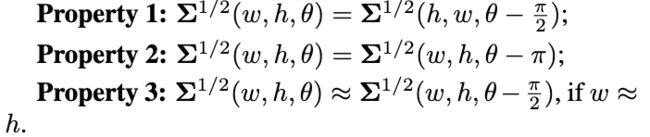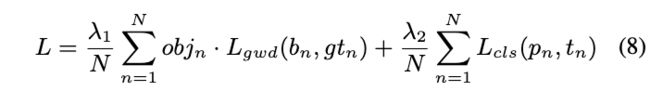GWD：基于高斯Wasserstein距离的旋转目标检测 | ICML 2021

  论文详细描述了当前旋转目标检测的主要问题，提出将旋转回归目标定义为高斯分布，使用Wasserstein距离度量高斯分布间的距离用于训练。目前，常规目标检测也有很多将回归转化为概率分布函数的做法，本文有异曲同工之妙，值得阅读

来源：晓飞的算法工程笔记 公众号

论文: Rethinking Rotated Object Detection with Gaussian Wasserstein Distance Loss

• 论文地址：https://arxiv.org/abs/2101.11952
• 论文代码：https://github.com/yangxue0827/RotationDetection

Introduction

---

  任意朝向的目标在检测数据集中无处不在，相对于水平的目标检测，旋转目标检测仍处于起步阶段。目前，大多数SOTA研究都集中于回归目标的旋转角度，而解决旋转角度则带来新的问题：i) 指标与损失不一致。ii) 旋转角度回归区间不连续。 iii) 方形问题。事实上，以上的问题还没有很好的解决方案，这会极大地影响模型的性能，特别是在角度在范围边界的情况。

  为了解决上述问题，论文提出了GWD方法，首先使用二维高斯分布来对旋转目标进行建模，然后使用Gaussian Wasserstein Distance(GWD)来代替不可微的旋转IoU，根据GWD计算loss值，这样就将模型训练和度量标准对齐了。
  论文的主要贡献有以下几点：

• 总结了旋转目标检测的三个主要问题。
• 使用Gaussian Wasserstein Distance(GWD)描述旋转bbox间的距离，再用GWD计算代替IoU损失的loss，且是可微的。
• GWD-based损失能够解决旋转角度范围不连续问题和方形问题，且对bbox的定义方式没有要求。
• 在多个公开数据集上进行测试，论文的方法均有不错的表现。

Rotated Object Regression Detector Revisit

---

Bounding Box Definition

  图2展示了两种旋转bbox的定义方式：OpenCV形式$D_{oc}$和长边形式$D_{le}$，前者的角度为$h_{oc}$和横坐标的夹角$\theta \in [-90^{\circ },0^{\circ })$，后者的角度则为长边与横坐标的夹角$\theta \in [-90^{\circ },90^{\circ })$，两种定义可以进行相互的转换(不考虑中心点)：

  两种表示方法的主要差异在于边顺序和角度$(h,w,\theta )$，相同的bbox用不同的表达方式，可能需要交换边的顺序或角度加减90。在现在很多的研究中，将模型的设计与bbox的定义进行耦合来避免特定的问题：如$D_{oc}$可避免方形问题，$D_{le}$可避免边交换问题。

Inconsistency between Metric and Loss（指标与损失不一致问题）

  IoU是检测领域的重要评测指标，但在实际训练中使用的回归损失函数(如$l_n$-norms)与评测指标往往存在不一致的问题，即更小的损失值并不等于更高的性能。目前，不一致问题在水平目标检测领域已经有了一些应对措施，如DIoU和GIoU。而在旋转目标检测领域，由于角度回归的加入，使得不一致问题更加突出，但目前仍没有很好的解决方案，论文也列举了一些例子来对比IoU损失和smooth L1损失：

• Case 1: 角度差值与损失值之间的关系，曲线几何都是单调的，但只有smooth L1曲线是凸曲线，能优化到全局最优解。

• Case 2:长宽比差异与损失值之间的关系，smooth-l1损失值是固定的(主要来自于角度差异)，而IoU损失则随着横轴剧烈变化。

• Case 3:中心点偏移对损失值的影响，曲线都是单调的，但smooth L1曲线与差值大小没有高度一致。

  从上面的分析可以看出，在旋转目标检测领域，IoU损失更能填补评判准则与回归损失间的差异。但很遗憾，在旋转目标检测领域，两个旋转bbox间的IoU计算是不可微的，不能用于训练。为此，论文基于Wasserstein distance提出可微的损失来替代IoU损失，顺便也可以解决旋转角度回归区间不连续问题和方形问题。

Boundary Discontinuity and Square-Like Problem（旋转角度回归区间不连续以及方形问题）

  上图的Case1-2总结了旋转角度回归区间不连续问题，以以OpenCV形式的Case 2为例，对于anchor$(0,0,70,10,-90^{\circ })$以及GT$(0,0,10,70,-25^{\circ })$，存在两种回归的方法：

• way1逆时针旋转一个小角度即可，预测结果为$(0,0,70,10,-115^{\circ })$，但由于角度的周期性(PoA)和边顺序交换(EoE)，若使用smooth L1损失函数，这个结果与GT间会产生巨大的损失值。另外，这个角度也超出了预定的角度范围。
• 选择way2则需要在缩放宽高的同时，顺时针旋转一个大的角度。

  上述的问题通常出现在anchor和GT的角度在角度范围的边界位置时，当anchor和GT的角度不在边界位置时，way1则不会产生巨大的损失值。因此，对于smooth-L1，边界角度和非边界角度的最优处理会太一致，这也会阻碍模型的训练。

  方形问题主要出现在使用长边形式的检测方法中，由于方形目标没有绝对的长边，长边形式对方形目标的表达本身就不唯一。以Case3为例，存在anchor$(0,0,45,44,0^{\circ })$以及GT$(0,0,45,43,-60^{\circ })$，way1可以顺时针旋转一个小角度变成位置与GT一致的$(0,0,45,43,30^{\circ })$。但由于角度差距较大，way1会产生较高的回归损失。因此，需要像way2那样逆时针旋转较大的角度。造成方形问题的主要原因并不是前面提到的PoA和EoE，而是度量标准和损失计算的不一致导致的。

The Proposed Method

---

  经过上述的分析，论文希望新的旋转目标检测方法的回归损失函数满足以下几点：

• Requirement1: 与IoU度量标准高度一致。
• Requirement2: 可微，允许直接学习。
• Requirement3: 对角度回归范围的边界场景更为平滑。

Wasserstein Distance for Rotating Box

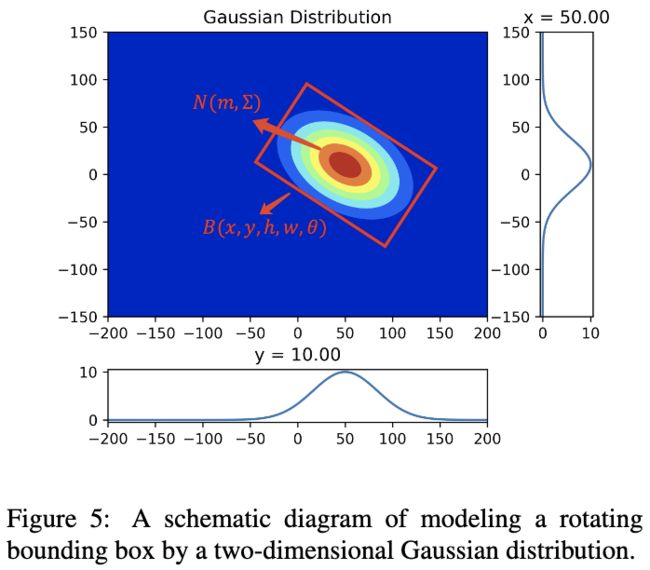
  目前大多数IoU损失都可认为是距离函数，基于此，论文基于Wasserstein distance提出新的回归损失函数。首先，将旋转bbox$\mathcal{B}(x,y,h,w,\theta )$转化为2-D高斯分布$\mathcal{N}(m,\sum )$：

  $R$为旋转矩阵，$S$为特征值的对角向量。对于${\mathbb{R}}^n$上的任意两个概率测度$\mu$和$\upsilon$，其Wasserstein距离$W$可表达为：

  公式2对所有的随机向量组合$(X,Y)\in {\mathbb{R}}^n\times {\mathbb{R}}^n,X\sim \mu ,Y\sim \upsilon$进行计算，代入高斯分布$d:=W(\mathcal{N}(m_1,{\sum }_1);\mathcal{N}(m_2,{\sum }_2))$，转换得到：

  特别要注意：

  考虑在可交换的情况(水平目标检测)${\sum }_1{\sum }_2={\sum }_2{\sum }_1$下，公式3可转换为：

  $\parallel {\parallel }_F$为Frobenius范数，这里的bbox均是水平的，公式5近似于$l_2$-norm损失，表明Wasserstein距离与水平检测任务中常用的损失一致，能够用于回归损失。这里的公式推算比较复杂，有兴趣的可以看看参考文献。

Gaussian Wasserstein Distance Regression Loss

  论文采用非线性转化函数$f$将GWD映射为$\frac{1}{\tau +f(d^2)}$，得到类似于IoU损失的函数：

  前面的曲线图也描述了使用不同非线性函数$f$下的损失函数曲线，可以看到公式6十分贴近IoU损失曲线，也能度量无相交的bbox。因此，公式6显然可以满足Requirement1和Requirement2，下面开始分析Requirement3，先给出公式1的特性：

  根据特性1可知，GWD损失函数对于OpenCV形式和长边形式是相等的，即模型不需要固定特定bbox表达形式进行训练。以Case2的Way1为例，GT$(0,0,70,10,65^{\circ })$和预测$(0,0,70,10,-115^{\circ })$拥有相同的均值$m$和方差$\sum$，GWD损失函数不会输出较大的损失值。而根据特性2和特性3，Case2和Case3的way1同样不会产生较大的损失值，所以GWD损失函数也满足Requirement3。
  整体而言，GWD在旋转目标检测的优势有以下几点：

• GWD使得bbox的不同定义形式相等，保证模型能够专注于准确率提升，不需要顾忌bbox的定义形式。
• GWD是可微的IoU损失替代方案，与检测指标高度一致。而且，GWD可以度量无相交bbox间的距离，类似于GIoU和DIoU的特性。
• GWD避免了旋转角度回归区间不连续问题和方形问题，降低了模型的学习难度。

Overall Loss Function Design

  论文将RetinaNet作为基础检测器，bbox表示为$(x,y,w,h,\theta )$，实验主要采用OpenCV形式，回归目标定义为：

  变量$x$,$x_a$,$x^{\ast }$分布代表GT，anchor和预测结果，最终的多任务损失函数为：

  $N$为anchor数，$ob{j}_n$为前景或背景的指示器，$b_n$为预测bbox，$g{t}_n$为GT，$t_n$为GT的标签，$p_n$为预测标签，${\lambda }_1=1$和${\lambda }_2=2$为超参数，$L_{cls}$为focal loss。

Experiments

---

  对比其他针对特定问题的解决方案。

  在DOTA数据集上对比多个模型，论文还有很多其他实验，有兴趣的可以去看看。

Conclusion

---

  论文详细描述了当前旋转目标检测的主要问题，提出将旋转回归目标定义为高斯分布，使用Wasserstein距离度量高斯分布间的距离用于训练。目前，常规目标检测也有很多将回归转化为概率分布函数的做法，本文有异曲同工之妙，值得阅读。

 

参考内容

• Wasserstein distance between two Gaussians - https://djalil.chafai.net/blog/2010/04/30/wasserstein-distance-between-two-gaussians/
   
   
   

如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】